Simfonija 题解
Simfonija 题解
题意
给定两个长度为 \(n\) 的数组 \(A\) 和 \(B\)，你可以给 \(A\) 数组中的所有元素加上 \(X\)（这里 \(X\) 应该能是负数），并修改不超过 \(K\) 个元素，使得下列代数式最小：
思路
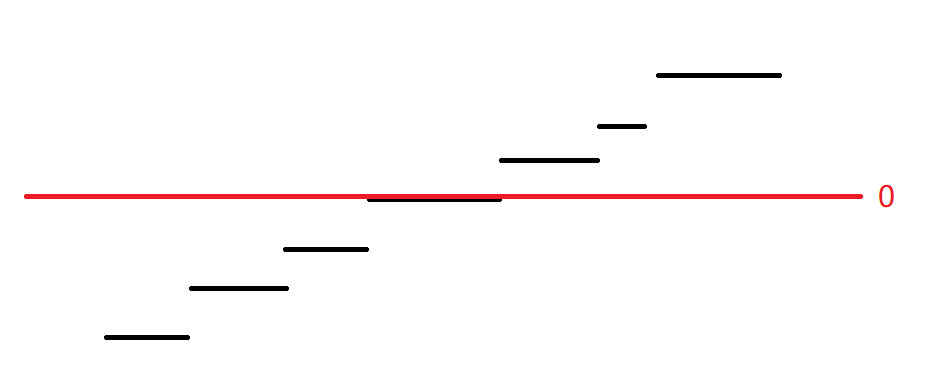
首先我们可以考虑 \(K = 0\) 的情况。因为是让差最小，所以我们并不关心 \(A_i\) 和 \(B_i\) 的值，只关心他们的差值即可。我们令 \(d_i\) 表示 \(B_i-A_i\)。如果没有 \(X\)，那么最后答案可以分为三部分：\(d_i < 0\)，\(d_i = 0\)，\(d_i>0\)。这时候，如果我们将 \(d_i\) 排序，会发现其值呈阶梯状分布，如图：
我们发现，答案就是这些黑线覆盖的面积。（想象一下从每一条黑线两侧延伸下来两条边，形成若干个矩形）
现在我们来考虑 \(X\)。我们发现，给 \(A\) 加上 \(X\) 相当于在上下平移这条红线，即 \(0\) 所在的位置。我们来考虑平移时面积的变化 ：
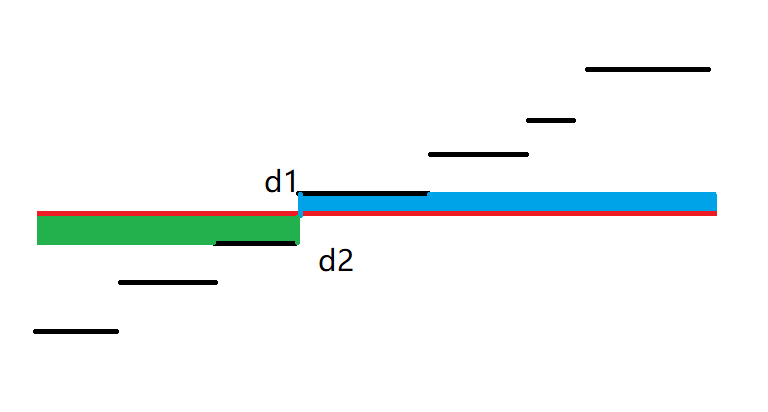
假如红线现在向上平移，设绿色面积为 \(s_1\)，蓝色面积为 \(s_2\)，两条黑线 \(d_1\) 与 \(d_2\) 交界处为 \(mid\)，我们发现，由于 \(mid\) 偏左，故向上平移时，左侧面积的增加量要小于右侧面积的减少量，所以向上平移答案会更优；同理，如果 \(mid\) 偏右，结果相反。不难想到，\(mid\)，也就是 \(0\) 值的位置，应该位于一个靠中间的位置。而这个位置就是中位数所在的位置。
但是我们还有 \(K\) 个数可以改动。显然，每次改动一定是让某个 \(B_i\) 等于 \(A_i\)，也就是让 \(d_i\) 为 \(0\)。另一个显然的事实是，无论 \(mid\) 选在哪里，需要改动的 \(d_i\) 一定是左右两侧连续的几个。那么，我们可以枚举左侧选 \(i\) 个，那么右侧就是 \(K-i\) 个。每次的中位数是单调不减的。我们只需要处理好每次改变 \(0\) 值点后答案的变化即可。
代码：
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+100;
const int M = 2e6+100, del = 2000000;
inline int read(){
int x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9') {if(ch == '-') f = -1; ch = getchar();}
while(ch>='0'&&ch<='9') {x = x*10+ch-48, ch = getchar();}
return x * f;
}
int n, K;
int a[N], b[N], d[N];
int e[N];
int ed[N];
int id[M<<1], idx;
int main(){
// freopen("simfonija.in", "r", stdin);
// freopen("simfonija.out", "w", stdout);
n = read(), K = read();
for(int i = 1; i<=n; ++i){
a[i] = read();
}
for(int i = 1; i<=n; ++i){
b[i] = read();
}
for(int i = 1; i<=n; ++i){
d[i] = b[i] - a[i];
}
sort(d+1, d+n+1);
for(int i = 1; i<=n; ++i){
if(i == n || d[i+1]!=d[i]){
id[d[i]+del] = ++idx;
ed[idx] = i;
}//预处理每段黑边的右端点。
}
int len = (n+1-K)/2;
int X = d[len];
long long ans = 0;
for(int i = 1; i<=(n-K); ++i){
ans+=abs(d[i]-X);
}//左侧不选的答案
int lst = X;
long long ret = ans;
for(int i = 1; i<=K; ++i){
int nX = d[i+len];
ans+= abs(d[n-K+i]-lst);//加上右侧弃选后增加的答案
ans-= abs(d[i]-lst);//减去左侧选后减少的答案
if(nX != lst){//如果中位数有变化，则 0 值线升高，要处理面积变化。
ans-=(1ll*((n-K+i)-ed[id[lst+del]]) * (nX-lst));
ans+=(1ll*(nX-lst)*(ed[id[lst+del]] - i));
lst = nX;
}
ret = min(ret, ans);//答案取最小的
}
printf("%lld\n", ret);
return 0;
}
