2023/7/20 模拟赛题解
2023/7/20 模拟赛题解
写在前面
这次比赛整体偏简单,而且部分分丰富,数据也不强,反正就是这次是运气好了。但是,还是要多加强思考的能力。
T1 古代龙人的谜题
题目描述
古代龙人手中共有n粒秘药,我们可以用1表示「古老的秘药」,其余的用0表示。他将它们排成一列。古代龙人认为平衡是美的,于是他问Mark能选出多少个「平衡的区间」。「平衡的区间」是指首先选出一个区间[L, R],在它内部选出一个中间点mid,满足L<mid<R,mid是「古老的秘药」,且区间[L, mid]和[mid, R]中「古老的秘药」个数相等。
思路
首先我们来考虑暴力:可以从左到右枚举中间点 \(i\), 以 \(i\) 为中心向左右扩展,答案能增加一当且仅当左区间和右区间的区间和相等;但是这样显然很慢。我们再往下看,发现,每次扩展并不需要一个一个点去扩展,因为增加的答案就是两边扩展的区间长度的乘积,也就是两个对称的 \(1\) 的位置中间的 \(0\) 的长度(注意,这里的对称指的是两个 \(1\) 到中间点 \(i\) 的范围内 \(1\) 的个数相等),这里给出图片方便理解:
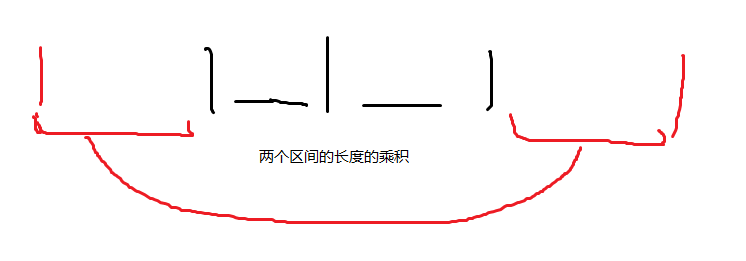
但是这样显然还是无法线性做。我们来考虑如何继续优化。
我们重新考虑上述过程,即枚举中心位置向左右拓展,每次贡献答案为区间长度乘积。我们发现,对于一个区间,会一直与右侧的一些区间造成贡献;反过来,每个区间,都会与左侧的一些区间造成贡献。而如果一个个枚举某个区间左侧的 \(1\) 作为中间点,会发现,能与该区间造成贡献的,一定是区间右端点 \(1\) 的编号奇偶性与该区间左端点的 \(1\) 奇偶性相同的区间,且每次都会累加。所以,我们就可以记录两个前缀和,每次用新区间的右侧长度去贡献答案即可。下图给出了每次枚举时答案的来源。注意处理开头与结尾的 \(0\),同时当前枚举到的 \(1\) 左右两侧的 \(0\) 要单独处理(因为不允许有长度为 \(1\) 的区间)。
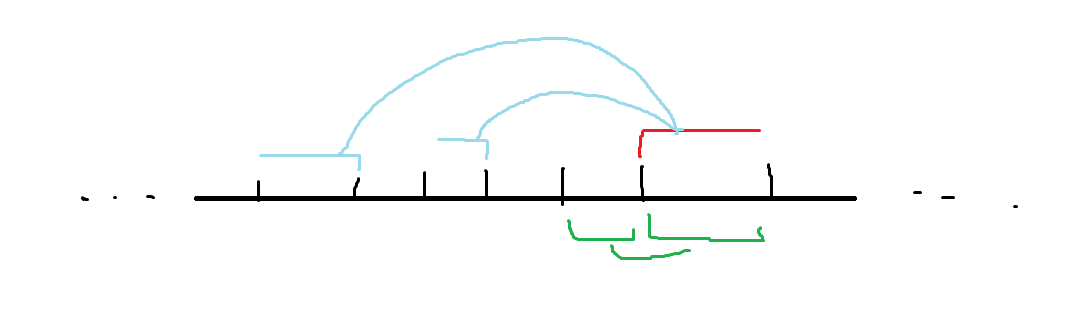
代码:
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6+100;
inline int read(){
int x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9'){
if(ch == '-') f = -1;
ch = getchar();
}
while(ch>='0'&&ch<='9') x = x*10+ch-48, ch = getchar();
return x * f;
}
int T;
int n;
char s[N];
ll cnt[2], cnt0, lst;
int now = 1;
ll ans;
int main(){
T = read();
n = read();
scanf("%s", s+1);
int st = 1;
while(s[st] == '0'){
++st, ++lst;
}
for(int i = st+1; i<=n; ++i){
if(s[i] == '1'){
ans+=lst*cnt0;
ans+=(cnt0+1)*cnt[now&1];
cnt[now&1]+=(lst+1);
lst = cnt0;cnt0 = 0;++now;
}
else ++cnt0;
}
ans+=cnt0*lst;
ans+=(cnt0+1)*cnt[now&1];
printf("%lld\n", ans);
return 0;
}
T2 指引
题意:
有 \(n\) 个旅者和 \(n\) 个传送门,每个旅者只能向右或向上走,每个传送门只能传送一名旅者,问最多可以传送多少旅者。
思路
场上想的做法是二分图(毕竟太明显了),但是最后一个点显然跑不动。有人说可以 KD-Tree 优化建图(反正我不会)。
正解应该是贪心(场上想了但是没细思考)。把人和门一起按横坐标降序、纵坐标降序排序,这样每次枚举到一个门,就加入数据结构,每次枚举到人,就把离他纵坐标最近的门给他。
考虑为什么这样做是对的。首先排序保证了后面枚举到的每个人的横坐标都不大于已有门的横坐标,而对于一个门,如果不给这个人而给其他人,显然其他人要么横坐标比他小,要么纵坐标比他小。考虑横坐标一样而纵坐标比他小的,这些人显然有可能有更多选择,所以门给这个人显然不劣;同样的,对于他左侧的人,如果这扇门能给他左侧的一个人,那另外那个人也可能会有更多选择;如果这扇门本来就不能给其他的人(纵坐标太高),那必须给这个人。总之,给这个人的答案不会劣于其他答案。这里可以用 multiset 维护。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+100;
struct point{
int x, y, type;
bool operator <(const point &b){
if(x == b.x){
return y>b.y;
}
return x>b.x;
}
}p[N<<1];
inline int read(){
int x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9'){if(ch == '-') f = -1; ch = getchar();}
while(ch>='0'&&ch<='9') x = x*10+ch-48, ch = getchar();
return x * f;
}
int Num;
int n;
multiset<int> s;
int ans;
int main(){
Num = read();
n = read();
for(int i = 1; i<=n; ++i){
p[i] = (point){read(), read(), 0};
}
for(int i = 1; i<=n; ++i){
p[i+n] = (point){read(), read(), 1};
}
n<<=1;
sort(p+1, p+n+1);
multiset<int> :: iterator it;
for(int i = 1; i<=n; ++i){
if(p[i].type){
s.insert(p[i].y);
} else{
it = s.lower_bound(p[i].y);
if(it != s.end()){
++ans;
s.erase(it);
}
}
}
printf("%d\n", ans);
return 0;
}
T3 碎片
题意
给定一个由大写字母组成的 \(n \times m\) 的矩阵,每次操作可以交换相邻的两行或两列,问能否将矩阵转换成一个中心对称图形?
思路
练习搜索的好题(
非常多的剪枝……反正这道题貌似就没有正解,都是瞎搞(正解貌似也是去搜索)。
这里首先要看到几个性质(非常有用):
- 矩阵合法的必要条件:对于所有行和所有列,除了中间位置(\(n\) 或 \(m\) 为奇数)可以单独成一行/列外,其他的每一行/列对应的那一行/列中的每个字母的数量应一致(即集合相同)(我就是靠这个性质水掉 95 pts 的)
- 对于一个已经中心对称的矩阵,将匹配的两行/列同时向里/外交换,矩阵仍合法
有了这两个行政我们就可以搜辣!
首先通过性质一可以直接排除很多不合法的方案,对于其他可能合法的方案,我们去搜索前一半要放哪些行,后一半放能和它匹配的,然后通过哈希来比较列于列是否可以匹配。复杂度玄学,但意外很快。
代码:
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
const int P = 233;
using namespace std;
const int N = 15;
inline int read() {
int x = 0, f = 1;
char ch = getchar();
while(ch<'0' || ch>'9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch>='0'&&ch<='9') x = x*10+ch-48, ch = getchar();
return x * f;
}
ull Ps[N];
int Num, T;
int n, m;
char s[N][N];
int ax[N][27], ay[N][27];//记录每一行/列字母的数量
int typ[N], tot;
int tx[N], ty[N];
bool check1(int x, int y) {
for(int i = 0; i<26; ++i) {
if(ax[x][i]!=ax[y][i]) return 0;
}
return 1;
}
bool check2(int x, int y) {
for(int i = 0; i<26; ++i) {
if(ay[x][i]!=ay[y][i]) return 0;
}
return 1;
}
int neH[N], neL[N];bool visH[N], visL[N];
bool ans;
ull hasha[N], hashb[N];
bool check(){
for(int i = 1; i<=m; ++i){
hasha[i] = 0;
hashb[i] = 0;
// Ps[0] = 1;
for(int j = 1; j<=n; ++j){
hasha[i] = hasha[i]*P+s[neH[j]][i];
}
for(int j = n; j>=1; --j){
hashb[i] = hashb[i]*P+s[neH[j]][i];
}
}
memset(visL, 0, sizeof(visL));
int cnt = 0;
for(int i = 1; i<=m; ++i){
if(visL[i]) continue;
for(int j = i+1; j<=m; ++j){
if(visL[j]) continue;
if(hasha[i] == hashb[j]){
cnt+=2;
visL[i] = 1, visL[j] = 1;
break;
}
}
}
if(m&1) return cnt>=m-1;
else return cnt == m;
}
void dfs(int pos, int lim){
if(pos>lim){
if(check()){
ans = 1;
}
return;
}
if((n&1)&&(pos == lim)){
for(int i = 1; i<=n; ++i){
if(visH[i]) continue;
neH[pos] = i;
break;
}
dfs(pos+1, lim);
}
for(int i = 1; i<=n; ++i){
if(visH[i]) continue;
visH[i] = 1;
neH[pos] = i;
for(int j = 1; j<=n; ++j){
if(visH[j]) continue;
if(tx[i] == tx[j]){
visH[j] = 1;
neH[n-pos+1] = j;
dfs(pos+1, lim);
if(ans) return;
visH[j] = 0;
}
}
visH[i] = 0;
}
}
int main() {
// freopen("data.txt", "r", stdin);
// freopen("my.out", "w", stdout);
Num = read();
T = read();
Ps[0] = 1;
for(int i = 1; i<=12; ++i){
Ps[i] = Ps[i-1]*P;
}
while(T--) {
n = read(), m = read();
memset(ax, 0, sizeof(ax));
memset(ay, 0, sizeof(ay));
memset(tx, 0, sizeof(tx));
memset(ty, 0, sizeof(ty));
for(int i = 1; i<=n; ++i) {
scanf("%s", s[i]+1);
}
for(int i = 1; i<=n; ++i) {
for(int j = 1; j<=m; ++j) {
++ax[i][s[i][j]-'A'];
}
}
for(int j = 1; j<=m; ++j) {
for(int i = 1; i<=n; ++i) {
++ay[j][s[i][j]-'A'];
}
}
tot = 0;
for(int i = 1; i<=n; ++i) {
if(tx[i]) continue;
if(!tx[i]) {
tx[i] = ++tot;
typ[tot] = 1;
}
for(int j = i+1; j<=n; ++j) {
if(tx[j]) continue;
if(check1(i, j)) {
tx[j] = tx[i];
++typ[tx[i]];
}
}
}
bool flag = 1;
bool is_failed = 0;
if(n&1) flag = 0;
for(int i = 1; i<=tot; ++i) {
if(flag && (typ[i]&1)) {
is_failed = 1;
break;
} else if(typ[i]&1) {
flag = 1;
}
}
if(is_failed) {
puts("NO");
continue;
}
tot = 0;
for(int i = 1; i<=m; ++i) {
if(ty[i]) continue;
if(!ty[i]) {
ty[i] = ++tot;
typ[tot] = 1;
}
for(int j = i+1; j<=m; ++j) {
if(ty[j]) continue;
if(check2(i, j)) {
ty[j] = ty[i];
++typ[ty[i]];
}
}
}
flag = 1;
if(m&1) flag = 0;
for(int i = 1; i<=tot; ++i) {
if(flag && (typ[i]&1)) {
is_failed = 1;
break;
} else if(typ[i]&1) {
flag = 1;
}
}
if(is_failed) {
puts("NO");
continue;
}
ans = 0;
memset(visH, 0, sizeof(visH));
dfs(1, (n+1)/2);
if(ans) puts("YES");
else puts("NO");
}
return 0;
}
T4 寻梦
updated 还是写了吧……
题面描述
\(N\) 名旅者背井离乡,前往他乡寻梦。
初始时,旅者 \(i\) 位于自己的家乡\(i\) 号城市。
每一天,位于\(i\) 号城市的所有旅者都会前往\(Ai\) 号城市,其中 \(Ai\) 是一个在整个过程中保持不变的量, 由于旅者迫切的寻梦欲望,我们规定\(Ai≠i\)。
现在小X 想要知道,是否存在至少一组满足条件的\(Ai\),使得在 \(K\) 天后,所有旅者会同时重新回到家乡(在这过程中旅者们同样可以途径自己的家乡)。
思路
首先很明显的一个套路就是把 \(A_i\) 和 \(i\) 连边,显然所有点最终会成为许多环,环的长度就是从起点走回到起点要花的时间。那么,问题就成功转化为能否把 \(n\) 个点连成若干个环(不允许有自环),每个环的长度都为 %K% 的因数。
然后这个问题就是一个分拆数问题,当然,你只需要找出一种方案即可。在 \(K\) 的质因数很少的时候可以直接爆搜,但是如果很多的话肯定是要 T 飞的。发现,当质因数只有一个的时候,直接判断即可;有两个的时候,可以用扩欧来解决;如果质因数个数大于 \(2\),由于 \(K\) 最大是 \(10^15\),最小的质因数一定不超过 \(10^5\),通过同余最短路判断即可。
代码就不放了,分类讨论搞得还特别丑,没啥可读性。

