李超线段树 学习笔记
李超线段树 学习笔记
今天模拟赛用到了李超线段树（但是本蒟蒻费了半天劲搞了个斜率优化拿到了 60pts 的好成绩 /kk），所以学习一下李超线段树刻不容缓（学会了我貌似也切不来那道题 qwq）。
引入
初中和高中我们都做过函数题吧，是不是有时候给你两根甚至几根直线，然后问你某个点的最值？当然，直线数很少的时候我们很容易做，甚至可以直接画图来看。现在我们要用计算机来解决这个问题，但是计算机可不会看图……怎么办呢？李超线段树出来力！
李超线段树是巨佬李超发明的一种数据结构，能在 \(\log_n\) （ \(n\) 为定义域大小，当然也可以通过动态开点来搞掉，不过都是后话了）的复杂度下求出几个一次函数在某一横坐标下，纵坐标的最大值。
普通李超线段树
思想
好吧李超线段树的思想其实也不是很复杂，简而言之就是，我们在每个节点（也就是区间）上，维护一条优势线段，其中优势线段的“优势”体现在区间中点处，也就是它在中点处能取到该点所有直线的最大纵坐标。
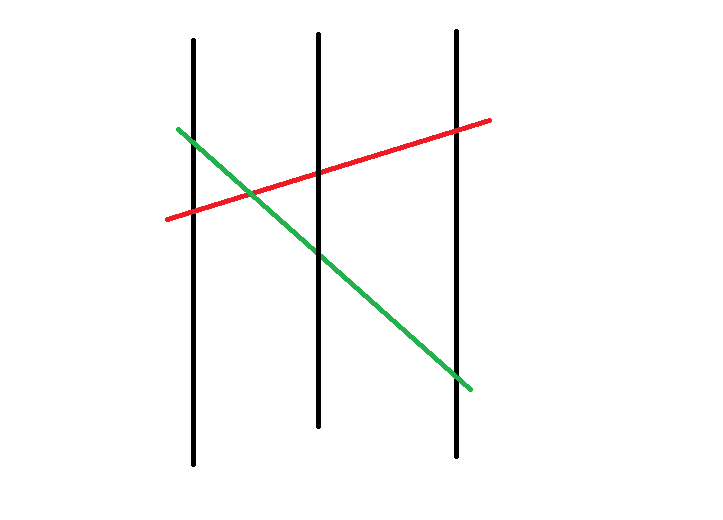
我们结合图来理解一下：
上图中，红色线段就是一条优势线段。
然后我们来考虑一下如何插入——
对于一个区间 \([l, r]\)，我们要插入线段（直线） \(a\)，分如下几种情况：
- 该区间没有线段，那么直接覆盖即可；
- 该区间已经有线段，但是 \(a\) 的左右端点都比原线段高，那么新线段就是优势线段，也是直接覆盖即可；
- 该区间已经有线段，而 \(a\) 的左右端点都比原线段低，那么就不作修改；
- 该区间已经有线段，而 \(a\) 与原线段 \(b\) 在区间内有交点，我们就讨论交点的位置：
- 如果交点在区间中点左侧（如上图），我们令中点处值较大的一条线段为优势线段。由于交点在中点左侧，所以在右半个区间中，优势线段仍然不会改变，所以不用修改；由于我们不能确定左侧区间内优势线段是谁，所以我们将非优势线段传递下去，修改左侧即可。
- 交点在区间中点右侧同理，只不过要继续修改的变成区间右侧。
那我们如何查询呢？
对于每个点的询问，我们必须要把包含该点的所有区间询问一次，取最大值。为什么呢？考虑这样一个问题：我们传递修改的过程中，只是把非优势线段传递下去，但是优势线段是无法下放的。也就是说，我们每个区间只是维护了一个相对优势的线段，来保证答案可能从中产生，而最终答案必须是从上往下都算一遍的。
例题
[洛谷 P4254 Blue Mary 开公司](P4254 [JSOI2008] Blue Mary 开公司 )
板子题，也没有啥细节，正好借这个题把板子总结一下。
代码：
#include<bits/stdc++.h>
#define ls tr<<1
#define rs tr<<1 | 1
#define LD long double
using namespace std;
const int N = 1e5+100, D = 5e4+100;
struct Line{
double k, b;//y = kx+b;
int l, r;//注意这里的l，r并不是记录区间的左右端点，而是记录线段的左右端点，这道题的线段都是直线，但是某些题需要对线段进行处理。
int flag;//标记区间有无线段。
}tree[N<<2];
int n, tot;
double calc(int x, Line tmp){
return tmp.k*x+tmp.b;
}//计算某个点的纵坐标值。
int cross(Line a, Line b){
return (b.b-a.b)/(a.k-b.k);
}//计算中点横坐标。
void build(int tr, int L, int R){
tree[tr] = {0, 0, 1, 50000, 0};//预处理。
if(L == R) return;
int mid = (L+R)>>1;
build(ls, L, mid);
build(rs, mid+1, R);
}
void modify(int tr, int L, int R, Line tmp){
if(tmp.l<=L && R<=tmp.r){//首先判断线段是否包含区间[L, R]。
if(!tree[tr].flag) tree[tr] = tmp, tree[tr].flag = 1;//情况1，直接覆盖。
else if(calc(L, tmp)>calc(L, tree[tr])&&calc(R, tmp)>calc(R, tree[tr])) tree[tr] = tmp;//情况2，覆盖。
else if(calc(L, tmp)>calc(L, tree[tr]) || calc(R, tmp)>calc(R, tree[tr])){//情况4
int mid = (L+R)>>1;
if(calc(mid, tmp)>calc(mid, tree[tr])){
swap(tree[tr], tmp);
}
if(cross(tmp, tree[tr])<=mid) modify(ls, L, mid, tmp);
else modify(rs, mid+1, R, tmp);
}
}else{//这一线段并不能代表区间内的情况，故要传递下去。
int mid = (L+R)>>1;
if(tmp.l<=mid) modify(ls, L, mid, tmp);
if(mid<tmp.r) modify(rs, mid+1, R, tmp);
}
}
double query(int tr, int L, int R, int x){//每走到一个区间就取一遍，求最大值。
if(L == R) return calc(x, tree[tr]);
int mid = (L+R)>>1;
double ans = calc(x, tree[tr]);
if(x <= mid) return max(ans, query(ls, L, mid, x));
else return max(ans, query(rs, mid+1, R, x));
}
char op[10];
int main(){
scanf("%d", &n);
build(1, 1, 50000);
while(n--){
scanf("%s", op);
if(op[0]=='Q'){
int day;
scanf("%d", &day);
int ans = ((int)query(1, 1, 50000, day))/100;
printf("%d\n", ans);
} else{
Line tmp;
scanf("%lf%lf", &tmp.b, &tmp.k);
tmp.l = 1, tmp.r = 50000;//这道题只对直线进行处理，所以左右端点可以看作定义域左右端点。
tmp.b-=tmp.k;
tmp.flag = 1;
modify(1, 1, 50000, tmp);
}
}
return 0;
}
还是一道板子题，但是细节还是有点多的xwx。注意有可能线段平行于 \(y\) 轴，所以要特别处理一下。（个人感觉这个板子更加简洁，比上面那个要好很多）。
#include<bits/stdc++.h>
#define ls tr<<1
#define rs tr<<1 | 1
using namespace std;
const int N = 39989, M = 1e9, NN = 1e5+100;
const double eps = 1e-10;
inline int read(){
int x = 0; char ch = getchar();
while(ch<'0' || ch>'9') ch = getchar();
while(ch>='0'&&ch<='9') x = x*10+ch-48, ch = getchar();
return x;
}
struct Line{
double k, b;
int l, r, id;
}lin[NN];
int tot;
int tree[N<<2];
double calc(Line tmp, int x){
return tmp.k*x+tmp.b;
}
int cross(int a, int b){
return floor((lin[a].b-lin[b].b)/(lin[b].k-lin[a].k));
}
bool cmp(int a, int b, int x){
double ta = calc(lin[a], x), tb = calc(lin[b], x);
return fabs(ta-tb)>eps?ta>tb:a<b;
}
void change(int tr, int L, int R, int id){
if(lin[id].l<=L && R<=lin[id].r){
if(!tree[tr]) tree[tr] = id;
else{
int mid = (L+R)>>1;
if(cmp(id, tree[tr], mid)) swap(id, tree[tr]);
if(L == R || fabs(lin[id].k-lin[tree[tr]].k)<eps) return;
if(cmp(id, tree[tr], L)) change(ls, L, mid, id);
else if(cmp(id, tree[tr], R)) change(rs, mid+1, R, id);
return;
}
} else{
int mid = (L+R)>>1;
if(lin[id].l<=mid) change(ls, L, mid, id);
if(lin[id].r>mid) change(rs, mid+1, R, id);
}
}
int query(int tr, int L, int R, int x){
if(L == R) return tree[tr];
int mid = (L+R)>>1, tmp;
if(x<=mid) tmp = query(ls, L, mid, x);
else tmp = query(rs, mid+1, R, x);
return cmp(tmp, tree[tr], x)?tmp:tree[tr];
}
int n;
int lastans;
inline int getx(int k){
return (k+lastans-1)%N+1;
}
inline int gety(int k){
return (k+lastans-1)%M+1;
}
int main(){
n = read();
while(n--){
int op = read();
if(op){
int xa = read(), ya = read(), xb = read(), yb = read();
xa = getx(xa), xb = getx(xb), ya = gety(ya), yb = gety(yb);
if(xa>xb) swap(xa, xb), swap(ya, yb);
tot++;
double tk, tb;
if(xa == xb){
tk = 0, tb = max(ya, yb);
} else{
tk = 1.0*(yb-ya)/(xb-xa);
tb = (ya-tk*xa);
}
lin[tot] = {tk, tb, xa, xb, tot};
change(1, 1, N, tot);
} else{
int x = read();
x = getx(x);
lastans = query(1, 1, N, x);
printf("%d\n", lastans);
}
}
return 0;
}
李超线段树不仅可以解决这些裸题，还能解决许多横坐标不单调的斜率优化的题目。其思想就是把表达式 \(f_i = f_j+a_ja_i+g_i+g_j\) 不去改成斜率优化的形式，而是把他看作求许多形如 \(f_i-g_i = a_ja_i+f_j+g_j\) 的直线中，在点 \(a_i\) 处的最大值，这时候就可以利用李超线段树来求解了。
动态开点李超线段树
我们刚才的李超线段树适用于定义域不大的情况，可如果定义域开到 \(10^{12}\) 这种的，就不太行了。区间很大，但线段很少，这说明我们浪费了很多空间，这时候就需要动态开点了！
我们拿一道例题为例，这是一道利用李超线段树优化 dp 的例子。
基站建设
首先我们可以画出来草图：
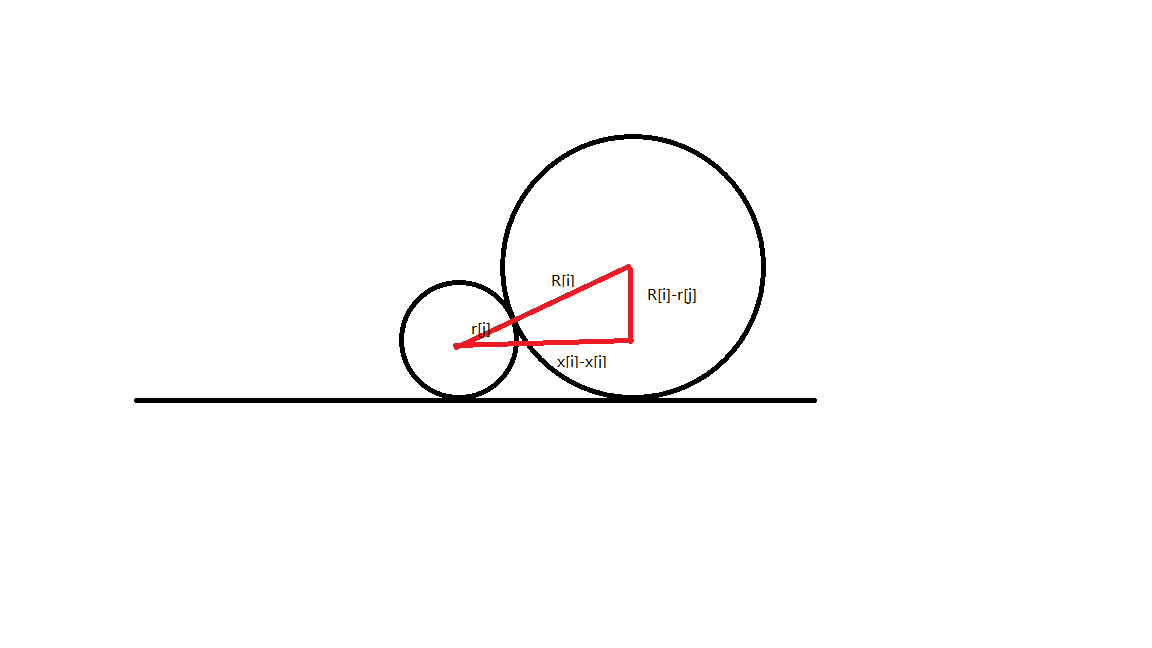
根据勾股定理，有 \((x_i-x_j)^2+(r'_i-r_j)^2 = (r'+r_j)^2\) ，整理得 \(\sqrt{r'_i} = \frac{1}{2 \sqrt{r_j}}(x_i-x_j)\)，因此有 \(f_i = f_j + v_i +\frac{1}{2 \sqrt{r_j}}(x_i-x_j)\)，再打开括号就是一个很经典的斜率优化式子。但是这里的横坐标 \(\frac{1}{2 \sqrt{r_j}}\) 并不是一个有单调性的东西，也就是说，我们维护的凸壳不能用单调队列来搞了。这时候就可以用李超线段树。具体来讲，我们把原式变为 \(f_i - v_i= \frac{1}{2 \sqrt{r_j}}x_i + f_j -\frac{1}{2 \sqrt{r_j}}x_j\) ，这样这道题就可以变为有一堆直线，\(k = \frac{1}{2 \sqrt{r_j}}\), \(b = f_j - \frac{1}{2 \sqrt{r_j}}x_j\)，查询其在 \(x_i\) 处的最小值。
需要注意的是并不一定要在最后一个点建设基站，需要把所有能覆盖目标点的都统计一遍，查找最小答案。
emm因为网上写的版本和我的普通版本都不太一样所以自己摸索着写了一个动态开点版本的（
代码：
#include<bits/stdc++.h>
#define LL long long
#define LD long double
using namespace std;
const int N = 5e5+100;
const LD eps = 1e-9;
const LD INF = 10000000000000;
struct Line{
int id; LD k, b;
}lin[N];
inline LL read(){
LL x = 0; char ch = getchar();
while(ch<'0' || ch>'9') ch = getchar();
while(ch>='0'&&ch<='9') x = x*10+ch-48, ch = getchar();
return x;
}
struct node{
int ls, rs, id;
}tree[N*44];
int idx;
double calc(Line tmp, LL x){
return tmp.k*x+tmp.b;
}
int cross(int a, int b){
return floor(lin[a].b-lin[b].b)/(lin[b].k-lin[a].k);
}
bool cmp(int a, int b, LL x){
double ta = calc(lin[a], x), tb = calc(lin[b], x);
return ta<tb;
}
void change(int &tr, LL L, LL R, int id){
if(!tr){
tr = ++idx;
tree[tr].id = id;
return;
}
LL mid = (L+R)>>1;
if(cmp(id, tree[tr].id, mid)) swap(id, tree[tr].id);
if(L == R || fabs(lin[id].k-lin[tree[tr].id].k) < eps) return;
if(cmp(id, tree[tr].id, L)) change(tree[tr].ls, L, mid, id);
else if(cmp(id, tree[tr].id, R)) change(tree[tr].rs, mid+1, R, id);
return;
}
LD query(int tr, LL L, LL R, LL x){
if(!tr) return INF;
if(L == R){
return calc(lin[tree[tr].id], x);
}
LD ret = calc(lin[tree[tr].id], x);
LL mid = (L+R)>>1;
if(x <= mid) ret = min(ret, query(tree[tr].ls, L, mid, x));
else ret = min(ret, query(tree[tr].rs, mid+1, R, x));
return ret;
}
int n;LL m;
LL pos[N], R[N], val[N];
LD f[N];
int root;
LD K(int x){
return 1.0/2/sqrt(R[x]);
}
LD B(int x){
return f[x]-1.0*pos[x]/2/sqrt(R[x]);
}
int main(){
n = (int) read(), m = read();
for(int i = 1; i<=n; ++i){
pos[i] = read(), R[i] = read(), val[i] = read();
}
f[1] = val[1];
lin[1] = (Line){1, K(1), B(1)};
change(root, 1, pos[n], 1);
for(int i = 2; i<=n; ++i){
f[i] = query(root, 1, pos[n], pos[i])+val[i];
lin[i] = (Line){i, K(i), B(i)};
change(root, 1, pos[n], i);
}
LD ans = INF;
for(int i = 1; i<=n; ++i){
if(R[i]+pos[i]>=m){
ans = min(ans, f[i]);
}
}
printf("%.3Lf\n", ans);
}
