斜率优化dp 学习笔记
斜率优化dp 学习笔记
引入
首先，我们考虑一种更简单的dp优化——单调队列优化。
比如，一个dp式形如：
我们发现，这个式子可以通过拆分（wgj：分离变量），变形成如下式子：
怎么样？我们发现，取最小值的这一项只与 \(j\) 有关，其余项只与 \(i\) 有关，那么我们可以想办法搞出 \(dp_j+f_j\) 的最小值，然后直接转移即可。我们发现，\(j\) 是在一个区间内的，那取最小值就转化为一个滑动窗口问题，使用单调队列即可。
总结一下，如果dp式中的元素可以分类，即一部分只与 \(i\) 有关，另一部分只与 \(j\) 有关，并且 \(j\) 有区间范围，区间单调右移，这样的dp就可以采用单调队列优化掉一层枚举。
但是，有时候，dp式子中的某一项既与 \(i\) 有关，又与 \(j\) 有关，例如以下dp式：
这时候你就完蛋了你就会痛苦的发现，单调队列不太行xwx。因为对于这个函数，我们很难直接找出最优决策点。
这时候，我们引入斜率优化。
斜率优化
Part 1：推式子
我们就题来谈 [APIO2010] 特别行动队
首先，这个题的dp式子很显然。我们设 \(s\) 为 \(x\) 的前缀和数组，\(dp_i\) 表示到第 \(i\) 个人，分组后的最大和，那么有：
然后，我们对它进行化简：
关于 \(i\) 的部分，我们可以当作常量提出去，令这部分为 \(g_i\)；剩下的部分中，一部分只与 \(j\) 有关，我们令这部分为 \(f_j\)，这样，式子变为：
这时候，我们来看一下 \(\max\) 内部的部分。我们不妨设 \(f_1-2as_is_1 \leq f_2 -2as_is_2\)，那么经过移项，有：
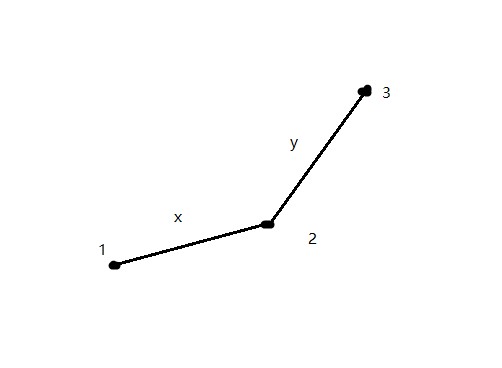
这样子，我们会发现一些内幕。如果平面直角坐标系中有两个点 \(A(s_1, f_1)\)，\(B(s_2, f_2)\)，那么上述式子等价于过 \(A\) 和 \(B\) 两点的直线的斜率。
Part 2：合法点集斜率单调性
我们总结一下上一个部分的结论：如果两个点连线的斜率不小于 \(2as_i\)，那么前面这个点对应的 \(j\) 就不是最优决策点；反之，后者对应的 \(j\) 不是最优决策点。
我们考虑三个点的简化情况，假设 \(1\) 号点到 \(2\) 号点的斜率为 \(x\)，\(2\) 号到 \(3\) 号点斜率为 \(y\)，令 \(x<y\)，\(k = 2as_i\)：
我们发现，\(2\) 号点一定不是最优决策点。因为它为最优点的充要条件是 \(y<k\) 并且 \(x \geq k\)，而 \(x < y\)。
那么，我们就可以宣：\(2\) 号点你废了！抹（ma）走！
扩展一下：如果我们现在有很多个点，而这个点集中，如果存在三个横坐标递增的点，使得前两个点的斜率小于等于后两个点的斜率，那么可以删掉中间的点。
所以，如果我们处理出一个不可删点集的斜率数组（也就是最终要挑选出最优决策点的点集），那这个数组必然是单调递减的。
Part 3 找最优决策点
那这样，我们就可以二分来查找最优决策点。
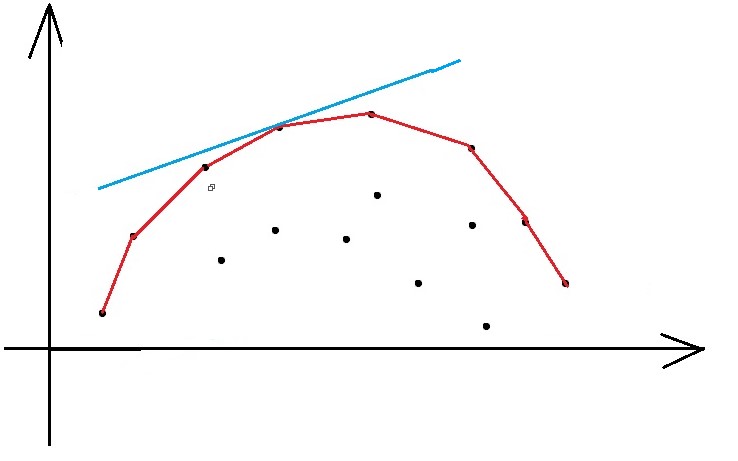
其实，如果我们画图来看，会发现上述过程中，我们维护了一个凸壳；
而找最优决策点，实际上就是令一条斜率为 \(k\) 的直线去切这个凸壳，切点即为最优决策点。
Part 4 另一个视角
我们可以以另一种方式来理解这一过程。再回到刚才的 dp 式子：
既然斜率为 \(2as_i\)，我们让 \(s_j\) 作为自变量，\(f_j\) 作为因变量，移项后会发现：
不难看出，这是一个直线方程。又因为斜率已知，所以这个方程只需要另一个点 \((s_j, f_j)\)就能确定，我们又发现，这条直线在 \(y\) 轴上的截距，恰巧就和答案有关；而 \(g_i\) 为常数，那么我们只需要令截距最大，那么答案就最大。
换句话说，我们现在就知道了，Part 3 中那条斜率为 \(2as_i\) 的直线是什么了。这样也能解释另一个问题，那就是当队列中只有一个点的时候如何求解，那就是令这条直线穿过这个点，因为你找不到另一个点使直线截距最大了。
Part 5 代码实现
在这道题中，可以省略二分这一步。为什么呢？因为这道题的 \(k\) 是单调递减的，所以我们每次只需要把队头斜率斜率比 \(2as_i\) 大的弹走，留下的队头就是最优决策点。
至于在队尾加入元素，我们维护上凸包，每次比较队尾的两个元素的斜率和队尾与 \(i\) 点的斜率，如果后者大于前者，就弹队尾。
注意有些细节：求斜率必须要有两个点，所以要初始化队列头尾指针为 \(0\)，这样当队列为空时，能保证队列中仍存在一个点。
#include<bits/stdc++.h>
#define LD long double
#define ll long long
using namespace std;
const int N = 1e6+100;
inline ll read(){
ll x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9'){
if(ch == '-') f = -1;
ch = getchar();
}
while(ch>='0'&& ch<='9'){
x = x*10+ch-48;
ch = getchar();
}
return x * f;
}
int n, L;
ll s[N];
ll a, b, c;
ll dp[N];
LD q[N];
int lq , rq;
LD getx(int x){
return s[x];
}
LD gety(int x){
return a*s[x]*s[x]-b*s[x]+dp[x];
}
LD getk(int x, int y){
return (gety(y)-gety(x))/(getx(y)-getx(x));
}
int main(){
scanf("%d", &n);
scanf("%lld%lld%lld", &a, &b, &c);
for(int i = 1; i<=n; ++i){
s[i] = read();
s[i]+=s[i-1];
}
for(int i = 1; i<=n; ++i){
while(lq<rq&&2*s[i]*a<=getk(q[lq], q[lq+1])) lq++;
int j = q[lq];
dp[i] = dp[j]+a*(s[i]-s[j])*(s[i]-s[j])+b*(s[i]-s[j])+c;
while(lq<rq&&getk(q[rq-1], q[rq])<=getk(q[rq], i)) rq--;
q[++rq] = i;
}
printf("%lld\n", dp[n]);
return 0;
}
例题++
拿到题，我们先推式子——
\(m^2s^2 = m^2\frac{1}{m} \sum_{i = 1}^{m}{(x_i - \bar{x})^2}\)
我们设所有 \(x_i\) 的和（即起点到终点的路程长）为 \(sum\)，将 \(m\) 乘进去，有：
\(m^2s^2= \frac{1}{m} \sum_{i = 1}^{m}{(mx_i-sum)^2}\)
将完全平方式展开：
\(m^2s^2= \frac{1}{m} (\sum_{i = 1}^{m}{m^2x_i^2}+\sum_{i = 1}^{m}sum^2-\sum_{i = 1}^{m}(2sumx_i))\)
而
\(sum = \sum_{i = 1}^{m}x_i\)
所以
\(m^2s^2= m\sum_{i = 1}^{m}x_i^2-sum^2\)
我们发现，\(sum^2\) 是常数，唯一会影响结果的部分就是 \(x_i^2\)，因为你不知道休息站设在哪里。这样一来，我们思路就清晰了。发现 \(x_i\) 可以前缀和处理，设前缀和数组为 \(c\)；设 \(f_{i, k}\) 表示当前在第 \(i\) 个分界点，且在这里设立一个休息站，总共已经设立了 \(k\) 个休息站（包括 \(i\) 处这一个），那么有转移（ \(m\) 可以最后再乘）：
我们可以直接暴力枚举 \(j\)，这样转移有80pts；
考虑优化。
我们继续整理式子，将它打开，发现：
\(f_{j, k-1} + c_j^2 = 2c_ic_j+f_{i, k}-c_i^2\)
到这里，你就偷着乐你会发现，这个就是斜率优化的样子。这里的斜率是单调递增的，所以可以直接 O(n) 处理。
代码：
#include<bits/stdc++.h>
#define ll long long
#define LD long double
using namespace std;
const int N = 3050;
inline int read(){
int x = 0; char ch = getchar();
while(ch<'0' || ch>'9'){ch = getchar();}
while(ch>='0'&&ch<='9'){x = x*10+ch-48; ch = getchar();}
return x;
}
int n, m;
int c[N];ll s[N];
ll f[N][N];
int q[N], lq, rq;
void init(){
lq = rq = 1;
}
inline LD X(int x){
return c[x];
}
inline LD Y(int x, int k){
return f[x][k-1]+c[x]*c[x];
}
inline LD K(int x, int y, int k){
return (Y(y, k)-Y(x, k))/(X(y)-X(x));
}
int main(){
n = read(), m = read();
for(int i = 1; i<=n; ++i){
c[i] = read()+c[i-1];
f[i][1] = c[i]*c[i];
//初始化，只建立一个休息站，其贡献就是到起点距离的平方。
}
for(int k = 2; k<=m; ++k){
init();
q[1] = k-1;
/*
注意这里！首先，下一个循环要从k开始（休息站不可能多于分界点数）
所以第一个转移一定是从 f[k-1][k-1]来的，故q[1]应为 k-1。
*/
for(int i = k; i<=n; ++i){
while(lq<rq&&K(q[lq], q[lq+1], k)<=2*c[i]) ++lq;
int j = q[lq];
f[i][k] = f[j][k-1]+(c[i]-c[j])*(c[i]-c[j]);
while(lq<rq&&K(q[rq-1], q[rq], k)>=K(q[rq], i, k)) --rq;
q[++rq] = i;
}
}
printf("%lld\n", f[n][m]*m-c[n]*c[n]);
return 0;
}
