CF 119D String Transformation 题解

emm不知道为啥会评黑……其实不难（虽然看了题解才想起来有哈希这玩意）。

题目给了一种翻转操作，乍一看无从下手，但是如果你画一画示意图，会发现很多东西。

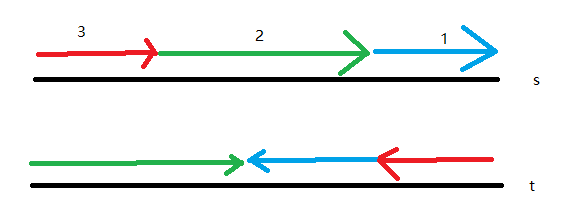
如图，我们用箭头表示方向，颜色表示三个不同的部分。这样看的话，我们发现，标号为 $2$ 的部分可以用 KMP 处理，但是 $1$ 和 $3$ 貌似没法处理。

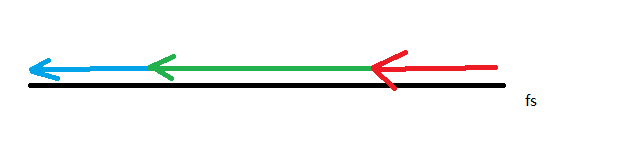
这时候，让我们把原串 $s$ 反过来看。我们让新串叫做 $fs$，怎么样，是不是有发现！ $t$ 和 $fs$ 的后缀部分都是 $3$ 号串，而 $1$ 号串部分我们可以用 KMP 来处理，剩下的我们只需要判断 $2$ 号串是否相同即可。这个可以用哈希表。因为要求 $i$ 最大，$j$ 最小，所以我们用 KMP 处理出 $1$ 号串的极左端点，从小到大枚举 $1$ 号串右端点的位置，这样就可以保证答案限制了。

但是，还没完。这里有个正确性的问题，那就是，我们处理出极长字串是否正确。为什么这样说？因为我们发现，题目要求 $j$ 最小，而我们处理出的极长字串其实是让 $j$ 变大了。但其实根本没必要担心，因为如果存在这样的一个串，那么答案会提前更新完毕。至于证明，可以自己画一画，标出相同的部分（才不是因为我懒呢）。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6+100;
const int pa = 23, pb = 233, ma = 998244353, mb = 1000000007;
int n;
 
ll hasha[2][N], hashb[2][N], spa[N], spb[N], hashc[N];
char s[N], fs[N];
char t[N];
int nxt2[N], nxt1[N];
int ansl = -1, ansr = -1;
void init(){
    spa[0] = spb[0] = 1; 
    for(int i = 1; i<=n; i++){
        hasha[0][i] = (hasha[0][i-1]*pa%ma+s[i])%ma;
        hasha[1][i] = (hasha[1][i-1]*pa%ma+t[i])%ma;
        hashc[i] = (hashc[i-1]*pa%ma+fs[i])%ma;
        spa[i] = spa[i-1]*pa%ma;
    }
    for(int i = 1; i<=n; i++){
        hashb[0][i] = (hashb[0][i-1]*pb%mb+s[i])%mb;
        hashb[1][i] = (hashb[1][i-1]*pb%mb+t[i])%mb;
        spb[i] = spb[i-1]*pb%mb;
    }
}
void check(int l, int r){
    if(ansl<l){
        ansl = l, ansr = r;
    }else if(ansl == l&&ansr>r){
        ansr = r;
    }
}
inline ll geta(int l, int r, int op){
    return ((hasha[op][r]-hasha[op][l-1]*spa[r-l+1]%ma)%ma+ma)%ma;
}
inline ll getb(int l, int r, int op){
    return ((hashb[op][r]-hashb[op][l-1]*spb[r-l+1]%mb)%mb+mb)%mb;
}
inline ll getc(int l, int r){
	return ((hashc[r]-hashc[l-1]*spa[r-l+1]%ma)%ma+ma)%ma;
}
void KMP(){
    int j = 0;
    for(int i = 2; i<=n; i++){
        while(j&&fs[j+1]!=fs[i]){
            j = nxt1[j];
        }
        if(fs[j+1] == fs[i])++j;
        nxt1[i] = j;
    }
    j = 0;
    for(int i = 1; i<=n; i++){
        while(j&&fs[j+1]!=t[i]){
            j = nxt1[j];
        }
        if(fs[j+1] == t[i]) j++;
        nxt2[i] = j;//求出1号串左端的极大位置。
    }
    for(int i = 1; i<n; i++){
        int pos = nxt2[i];
        if(!pos) continue;
        if(geta(i+1, n, 1) == getc(i+1, n)&&geta(1,i-pos, 1)==geta(n-i+1, n-pos, 0)&&getb(1,i-pos, 1)==getb(n-i+1, n-pos, 0)){
            check(n-i-1, n-pos);
        }
    }
 
}
int main(){
    cin.getline(s+1, 1000006);
    cin.getline(t+1, 1000006);
    n = strlen(s+1);
    int mtp = strlen(t+1);
    if(n ^ mtp){
    	puts("-1 -1");
    	return 0;
	}
    for(int i = 1; i<=n; i++){
        fs[i] = s[n-i+1];
    }
    init();
    KMP();
    printf("%d %d\n", ansl, ansr);
    return 0;
}