素数在两种常见情况下的标准最优算法
素数在两种常见情况下的标准最优算法
方法名称
-
相邻剪枝法
通过判断待验证数是否在6的两侧而进行剪枝(2与3除外),验证单个数字时常用。
下述代码中原型体现为prime_1()
-
素数筛法
依据每个素数的倍数不可能再为素数的原理,制素数表时常用。
下述代码中原型体现为prime_2()
代码测试模块
#include <iostream>
#include <cmath>
#include <ctime>
#include <cstring>
using namespace std;
const int SIZE = 2e7;
bool table[SIZE];
// 相邻剪枝法——单重样例判断
bool prime_1(int n)
{
if(n == 2 || n == 3)
return true;
if(n % 6 != 1 && n % 6 != 5)
return false;
for(int i = 5; i <= sqrt(n); i+=6)
{
if(n % i == 0 || n % (i+2) == 0)
return false;
}
return true;
}
// 相邻剪枝法——多重样例判断
void prime_1p()
{
for(int i = 2; i <= SIZE; i++)
{
table[i] = prime_1(i);
}
cout << "prime_1p completed." << endl;
}
// 素数筛选法——单重样例判断
bool prime_2(int n)
{
for(int i = 2; i <= SIZE; i++)
{
if(table[i])
{
for(int j = 2; j * i <= SIZE; j++)
{
table[i * j] = false;
}
}
}
return table[n];
}
// 素数筛选法——多重样例判断
void prime_2p()
{
for(int i = 2; i <= SIZE; i++)
{
if(table[i])
{
for(int j = 2; j * i <= SIZE; j++)
{
table[i * j] = false;
}
}
}
cout << "prime_2p completed." << endl;
}
int main()
{
memset(table, true, SIZE*sizeof(bool));
int start = clock();
prime_1p();
cout << "First statu use: " << clock() - start << endl;
memset(table, true, SIZE*sizeof(bool));
start = clock();
prime_2p();
cout << "Second statu use: " << clock() - start << endl;
memset(table, true, SIZE*sizeof(bool));
start = clock();
prime_1(SIZE);
cout << "Third statu use: " << clock() - start << endl;
memset(table, true, SIZE*sizeof(bool));
start = clock();
prime_2(SIZE);
cout << "Forth statu use: " << clock() - start << endl;
return 0;
}
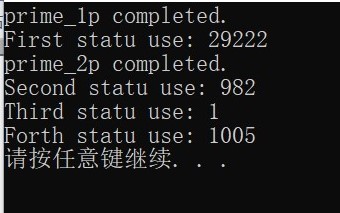
运行结果示例