EfficientNet & EfficientDet 论文解读

概述

总体而言，这两篇论文都在追求一件事，那就是它们名字中都有的 efficient。只是两篇文章的侧重点不一样，EfficientNet 主要时研究如何平衡模型的深度 (depth)、宽度 (width) 以及分辨率 (resolution) 以获得更好的性能，并使用了一个复合系数 (compound coefficient) 来统一调整模型的规模。EfficientDet 的亮点在于提出了 BiFPN （双向特征金字塔网络？），其实就是目标检测中的 neck 部分用于特征图的融合，然后在这个基础之上进行了跟 EfficientNet 的拼接并且加了分类和回归的 head，同样用复合缩放 (compound scale) 的方式进行调整。因此，先总结一下 EfficientNet 的工作。

EfficientNet

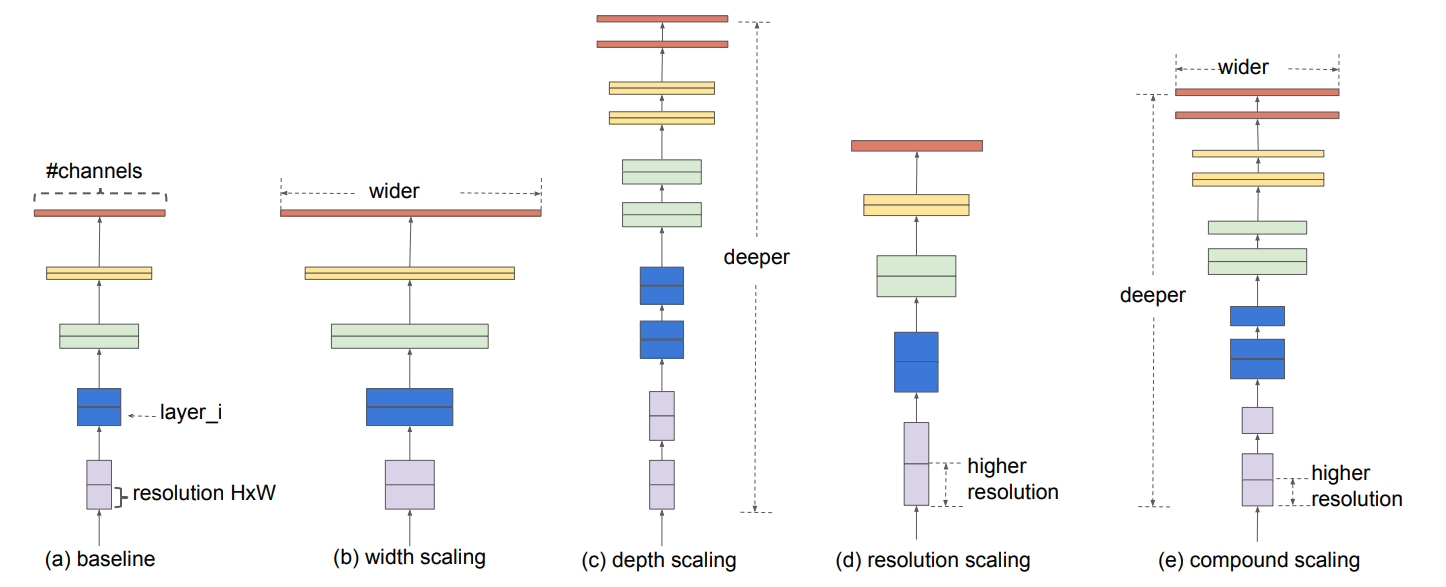
EfficientNet 的研究离不开上面那张图。但我们首先来介绍一下 EfficientNet 的思想：它会用统一的系数来调整深度、高度、分辨率。比如，这个系数为 \(N\)，那么如果我们想用 \(2^N\) 倍的计算资源来跑模型，就可以简单地将网络的宽度、深度以及图片尺寸分别扩大 \(\alpha^N,\beta^N,\gamma^N\) 倍（其中 \(\alpha,\beta,\gamma\) 是通过最初始的即没有进行缩放的模型来进行网格搜索出来的参数）。

问题的推导

第 \(i\) 层卷积层可以被定义为 \(Y_i = \mathcal{F}_i (X_i)\)，其中 \(\mathcal{F}_i\) 就是这个层进行的一系列操作，\(Y_i\) 是输出，\(X_i\) 是输入。那么卷积网络就可以使用下式来表达：

\[\mathcal{N} = \mathcal{F}_k \odot \dots \odot \mathcal{F}_2 \odot \mathcal{F}_1(X_1) = \bigodot_{j=1,\dots,k} \mathcal{F}_j(X_1) \]

其实表达的就是一个卷积层的输出作为另外一个卷积层的输入，然而卷积网络的层经常会被分成多个阶段，每个阶段共享同样的结构。例如，ResNet 有 5 个阶段，在每个阶段所有的层都有同样的卷积形式（除了第一层需要下采样以外）

\[\mathcal{N} = \bigodot_{i=1,\dots,s} \mathcal{F}_j^{L_i}(X_i) \]

\(\mathcal{F}_j^{L_i}\) 表示 \(\mathcal{F}_i\) 在阶段 \(i\) 中重复了 \(L_i\) 次。大多数的卷积网络主要关注如何设计最好的层结构 \(\mathcal{F}_i\)，而模型的缩放主要从网络的长度（深度）、宽度（通道）和分辨率着手，不会去改变 baseline 中预定义的 \(\mathcal{F}_i\)。虽然固定了 \(\mathcal{F}_i\) 的结构，但深度、宽度和分辨率依然有着很大的探索空间。EfficientNet 通过一个复合系数来调整所有层来到达缩减设计的空间的目的。

缩放维度

接着 EfficientNet 分别对不同的卷积网络不同的维度进行探索。

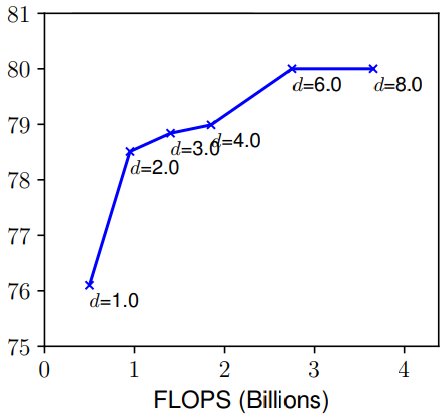
• Depth(d)： 一个网络的深度简而言之就是这个网络的层数。自从有了残差连接、BN 等手段来减轻较深网络的训练问题，比较深的网络就大量的出现比如：ResNet101、ResNeXt101 等，但是 ResNet1000 虽然比 ResNet101 多了许多层，准确度只有较少的提升。如上图所示，如果一味的增加深度，那么在非常深的情况，精度提升就不那么明显了。

 

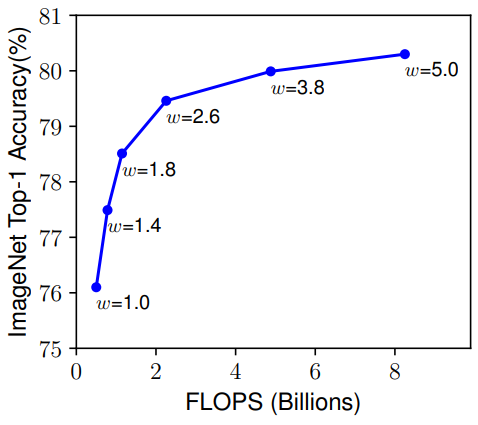
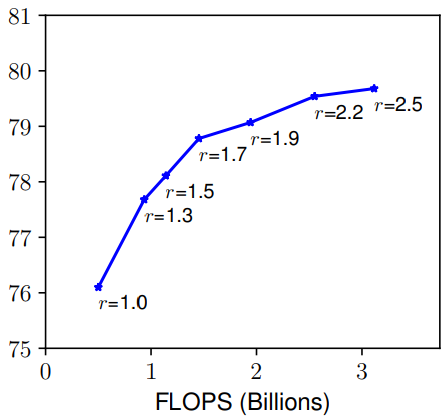
• Width(w) & Resolution(r)：一个网络的宽度是指其通道数，而分辨率就是输入图片的尺寸（简单理解），由上图也可以发现和深度有着同样的问题。总而言之，缩放网络宽度、深度和分辨率的任一尺度都可以改善精确度，但这种方法在模型更大的时候就没有效果了。

复合缩放 (Compound Scaling)

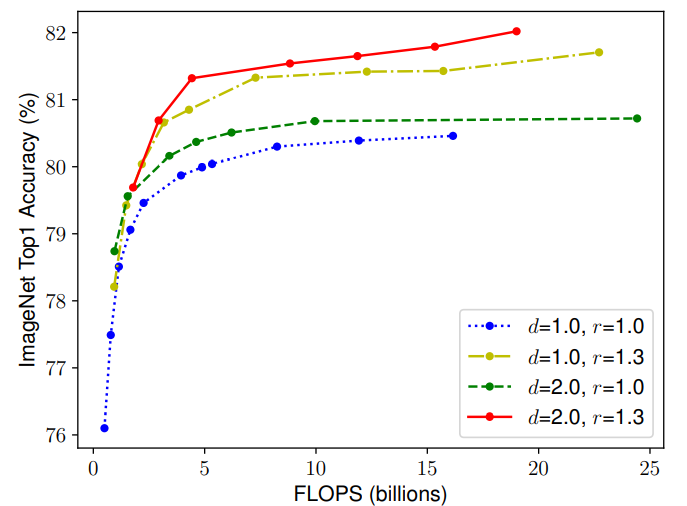
那么就很自然的思考到一个问题：在缩放一个维度的时候，是不是对另外一个维度也是有所影响的呢？比如，增加宽度有助于获取较大图片中相似的特征，所以分辨率更大的时候是不是应该考虑增加网络的宽度？如上图所示，当 r 越大的时候，将 d 也调大可以获得更好的性能。因此平衡网络的深度、宽度以及分辨率是至关重要的。

文章提出了一种复合缩放的方法，即用一个复合系数 \(\phi\) 来统一缩放网络的宽度、深度和分辨率：

\[\begin{aligned} d &= \alpha^{\phi} \\ w &= \beta^{\phi} \\ r &= \gamma^{\phi} \\ \mathrm{s.t.} & \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \end{aligned} \]

如之前所言，\(\alpha, \beta, \gamma\) 是通过网格搜索得到的。由于卷积操作的 FLOPs 和 \(d,w^2,r^2\) 是成正比的，因此使网络深度翻倍会使 FLOPs 翻倍，如果宽度和分辨率是原来的两倍，FLOPS 则会变为原来的 4 倍。由此可以计算，当三者整体为初始的 \(\phi\) 倍的时候，FLOPs 为初始的 \((\alpha \cdot \beta^2 \cdot \gamma^2)^{\phi} = 2^{\phi}\) 倍。

EfficientNet 结构

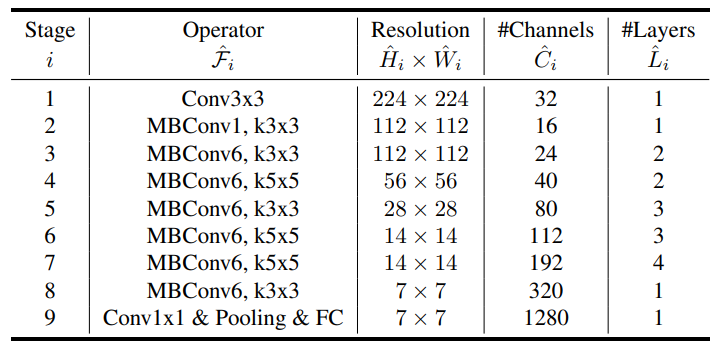
在设计 baseline 网络的时候，将 \(ACC(M) \times [FLOPS(m)/T]^w\)（即综合模型的准确度和浮点运算次数进行考虑）作为优化目标提出了 EfficientNet-B0，其主要由 MBConv (San-dler et al., 2018; Tan et al., 2019)组成，同时加入了 squeeze-and-excitation optimization 操作。通过网格搜索 \(\alpha=1.2, \beta=1.1, \gamma=1.15\) 是 EfficientNet-B0 最优参数，然后通过 \(\phi\) 进行调整得到 B1 到 B7 版本。

EfficientDet

在了解了 EfficientNet 后再来学习 EfficientDet 只需要明白 weighted bi-directional feature pyramid network (BiFPN) 的结构与它是如何配合 EfficientNet 形成 EfficientDet 的就行了。EfficientDet 基于之前的工作主要是针对一些特定的情况进行设计，提出是否可能设计一种可以缩放的同时具有高精度和高准去率的检测结构呢？这里面主要需要解决两个问题：

• efficient multi-scale feature fusion：FPN、PANet 等之前的工作将输入形成的多个特征图无差别的进行融合，然而不同的特征图对于每一层融合后的结果的贡献肯定是不一样。也就是之前没有对进行融合的特征图设置权重。

• model scaling: 这个问题其实 EfficentNet 已经解释了。

EfficientDet 解决上述问题分别使用 BiFPN 和 EfficientNet 进行解决。

问题的推导

多尺度特征融合指的是对不同分辨率的特征进行综合，这也是目标检测的 neck 部分。考虑一组多尺度特征 \(\vec{P}^{in} = (P^{in}_{l_1},P^{in}_{l_2},\dots)\)，其中 \(P^{in}_{l_i}\) 代表了 \(l_i\) 层的特征，事实上 neck 部分的工作就是找到一个转换的函数 \(f\) 输入一组特征图后得到另外一组特征图即 \(\vec{P}^{out} = f(\vec{P}^{in})\)。

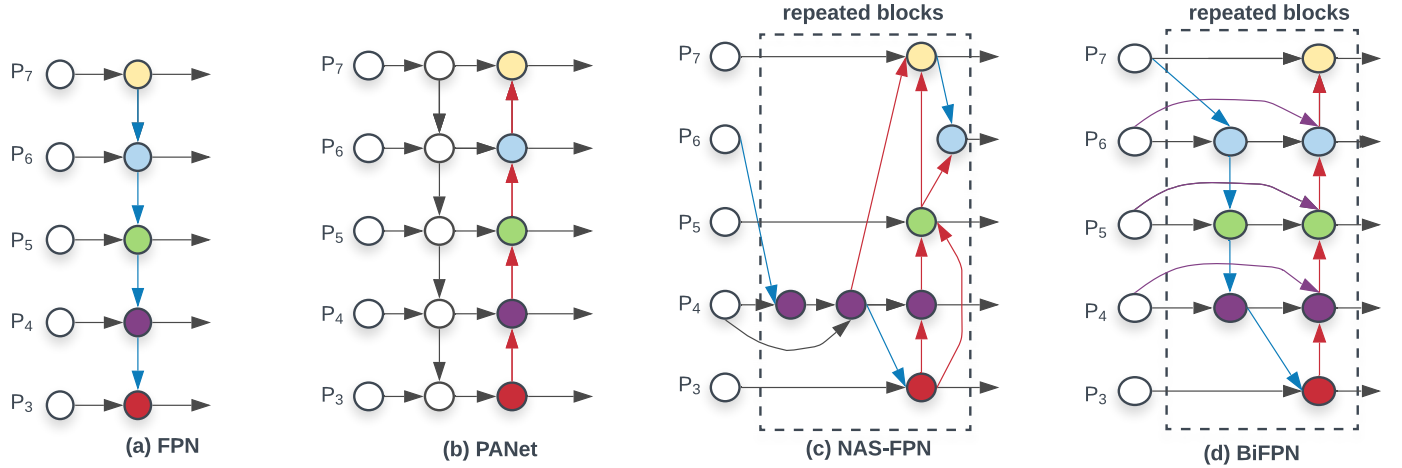
如上图，经典的 FPN 就是取了 level 3-7 的特征图作为输入 \(\vec{P}^{in} = (P^{in}_{3},\dots,P^{in}_{7})\) 其中 \(P^{in}_i\) 里面的 \(i\) 代表其分辨率为输入图片的 \(1/2^i\)。将上图中的 (a) 用公式表达则是：

\[\begin{aligned} P^{out}_{7} &= Conv(P^{in}_{7}) \\ P^{out}_{6} &= Conv(P^{in}_{6} + Resize(P^{out}_{7})) \\ & \dots \\ P^{out}_{3} &= Conv(P^{in}_{3} + Resize(P^{out}_{4})) \\ \end{aligned} \]

Resize 一般采用的上采样或者下采样，因此特征图的尺寸不一样所以需要调整后才能融合。但是注意在融合的时候 \(P^{in}_{6}\) 和 \(Resize(P^{out}_{7})\) 前面的系数都是 1，也是文章提到的无差别融合。很容易能够发现传统的 FPN 被只有一条信息流所限制，因此 PANet 添加了一条额外的自底而上的路径进行融合。

因此针对跨尺度连接：首先去除了只有一个输入的 node，因为一个 node 只有一个输入并没有特征融合，那么它对于针对不同特征融合的特征网络的贡献就比较少（可见(d)图的 \(P_2,P_7\)）。第二，新加了一条从原始输入到输出的边（即残差连接），这样的连接并不会消耗太多。

关于有权重的特征融合

这就是在最开始提的不同分辨率的特征图进行融合时，按照它们对输出应该有不同的贡献分配不同的权重，而不是像 FPN 和 PANet 一样无差别的融合。因此，文章讨论了几种权重融合的方式：

• Unbounded fusion: \(O = \sum_i w_i \cdot I_i\)
  上式中的权重时可以学习的参数。这种方式能以最少的计算资源能到达与其它方式相同的准确度，但是这种权重时无边界的，因此训练极为不稳定。

• Softmax-based fusion: \(O = \sum_i \frac{e^{w_i}}{\sum_j e^{w_j}}\)
  很简单，应用 softmax 函数将权重归一化到了 0 到 1 之间，不过在文章的 ablation 实验表明，其非常消耗 GPU 资源。

• Fast normalized fusion: \(O = \sum_i \frac{w_i}{\epsilon + \sum_j w_j}\)
  对每个权重应用 Relu 函数可以保证 \(w_i\) 大于 0，然后再使用 \(\epsilon\) 保证数值稳定，这样做也能使最终的权重介于 0 到 1 之间，而且这种方式比较简单，运行起来也比较有效率，因此叫做快速归一融合。

因此作为例子，BiFPN 的第六层就可以有下式计算，首先利用下一层的特征和第六层的输入计算第六层中间的结点：

\[P_6^{td} = Conv \Big(\frac{w_1 \cdot P_6^{in} + w_2 \cdot Resize(P_7^{in})}{w_1 + w_2 + \epsilon}\Big) \]

然后再利用第六层的输入、中间结点的输出与上一层的输出计算第六层的最终结果：

\[P_6^{out} = Conv \Big(\frac{w^{'}_1 \cdot P_6^{in} + w^{'}_2 \cdot P_6^{td} +w^{'}_3 \cdot Resize(P_5^{out})}{w^{'}_1 + w^{'}_2 + w^{'}_3 + \epsilon} \Big) \]

其他层的融合方式与上述类似，并且为了改善效率，文章使用了深度可分离卷积并对于每一个卷积添加了 BN 和激活函数。

EfficientDet 结构

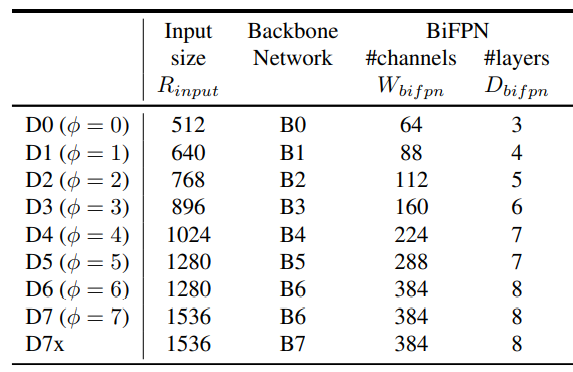
对于 EfficienDet 采用 EfficientNet-B0 到 B6 作为 backbone，而 neck 部分肯定是使用新提出了 BiFPN，而且对于 BiFPN 依然使用网格搜索得到一个最优的缩放因子，同样由 \(\phi\) 来进行控制：

\[W_{bifpn} = 64 \cdot (1.35^{\phi}), D_{bifpn} = 3 + \phi \]

\(W_{bifpn}\) 为通道数，并以 1.35 倍增长，\(D_{bifpn}\) 则为重复的次数。关于 head 部分，则不是我们关注的重点。而对输入图片的分辨率，则由下式控制：

\[R_{input} = 512 + \phi \cdot 128 \]

计算结果如下

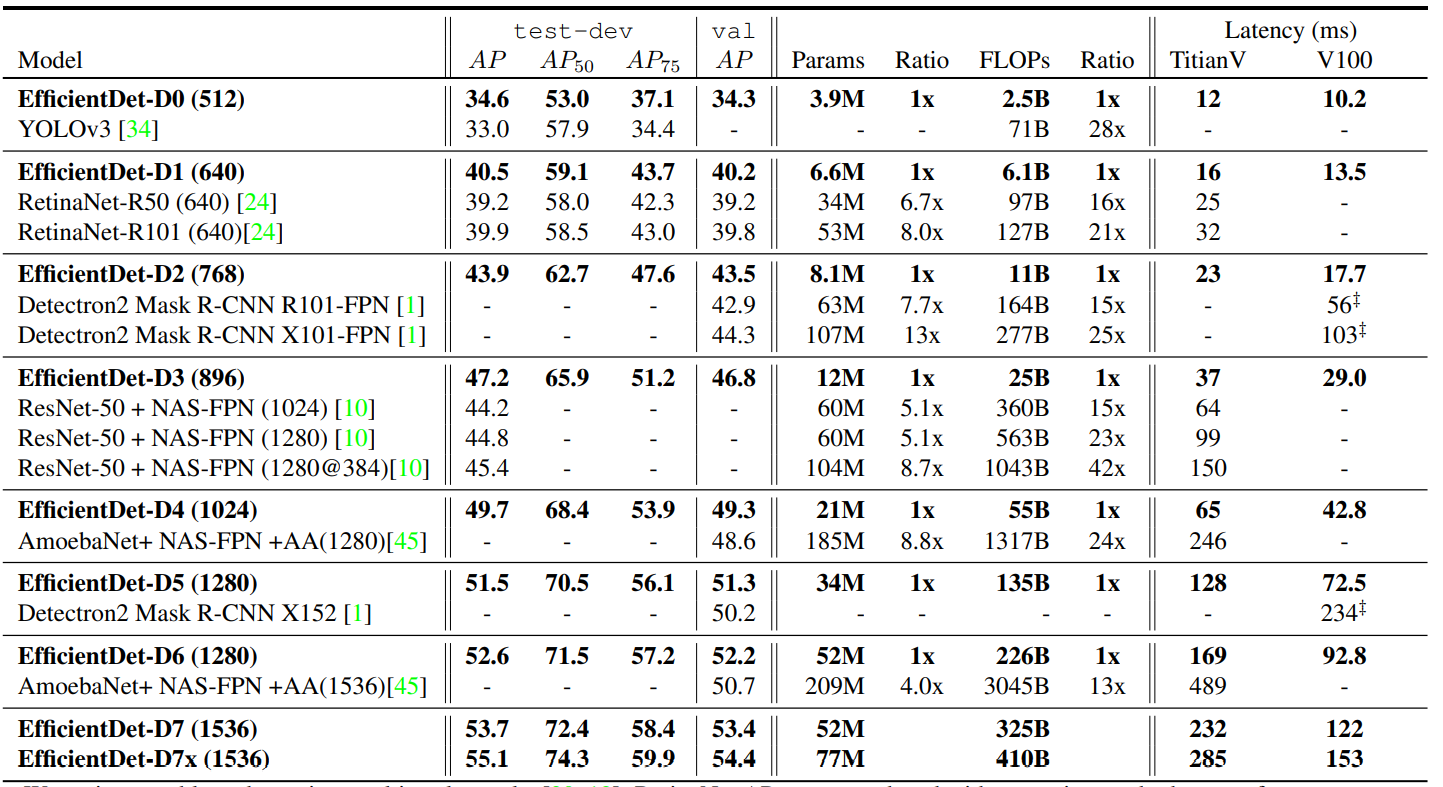
最后 EfficientDet 的对比实验结果如下：

EfficientNet-V2 To Be Continued~