Deep Unfolding Network for Image Super-Resolution (USRNet) 论文解读

Introduction

超分是一个在 low level CV 领域中经典的病态问题，比如增强图像视觉质量、改善其他 high level 视觉任务的表现。Zhang Kai 老师这篇文章在我看到的超分文章里面是比较惊艳我的一篇，首先他指出基于学习(learning-based)的方法表现出高效，且比传统方法更有效的特点。可是比起基于模型(model-based)的方法可以通过统一的最大后验框架来解决不同的 scale factors、blur kernels 和 noise levels 的问题，基于学习的方法看起来反而有些缺乏灵活性了。而文章提出了一种可以端到端的可训练的迭代模型，针对基于模型和基于学习的方法搭起了桥梁。

Unfolding optimization

根据最大后验(MAP)框架，HR 图像可以通过最小化以下能量函数得到：

\[E(x)=\frac{1}{2\sigma^2}\lVert y-(x \otimes k)\downarrow_s \rVert^2 + \lambda \Phi(x) \]

式中前面一项可以看作基于模型方法来进行超分，文章中称之为数据项。后面一项也称为先验项，可以理解为图片中的一些噪声。为了使其能够不断迭代，文章中使用了半二方分裂法(HQS)，原因有二：简洁性和快速收敛。HQS 常常解决上式优化问题引入辅助变量 z：

\[E_{\mu}(x)=\frac{1}{2\sigma^2}\lVert y-(z \otimes k)\downarrow_s \rVert^2 + \lambda \Phi(x) + \frac{\mu}{2}\lVert z-x \rVert^2 \]

其中 \(\mu\) 可以看作惩罚参数，上式可以不断迭代循环求解子问题来得到 x 和 z：

\[\begin{cases} z_k &= \mathrm{argmin}_z \lVert y-(z \otimes k)\downarrow_s \rVert^2 + \mu \sigma^2 \lVert z-x_{k-1} \rVert^2 \tag{#}\\ x_k &= \mathrm{argmin}_x \frac{\mu}{2} \lVert z_k - x \rVert^2 + \lambda \Phi(x) \end{cases} \]

显然第一式的 \(\mu\) 应该足够大，可以理解为 \(\lVert z-x_{k-1} \rVert\) 的权重，权重越大时，z 和 x 才会越接近。显然之前提到的数据项和先验项分别由上面二式进行求得。对于第一式，文中在圆周边界条件下卷积可以被求解的情况下使用了 FFT，根据论文Fast single image super-resolution using a new analytical solution for ℓ2-ℓ2 problems 该式有封闭形式的解：

\[z_k = \mathcal{F}^{-1}\bigg(\frac{1}{\alpha_k}\Big(d-\overline{\mathcal{F}(k)} \odot_{s} \frac{(\mathcal{F}(k)d)\Downarrow_s}{(\overline{\mathcal{F}(k)}\mathcal{F}(k))\Downarrow_s+\alpha_k}\Big)\bigg) \]

其中 \(d = \overline{\mathcal{F}(k)}\mathcal{F}(y \uparrow_s) + \alpha_k \mathcal{F}(x_{k-1}),\alpha_k \triangleq \mu_k \sigma^2\)，当上式的 \(s=1\) 时，相当于完全针对的 deblurring 问题。对于 # 式中的第二式实际上是一个噪声水平为 \(\beta_k \triangleq \sqrt{\lambda / \mu_k}\) 的去噪问题。

Deep unfolding network

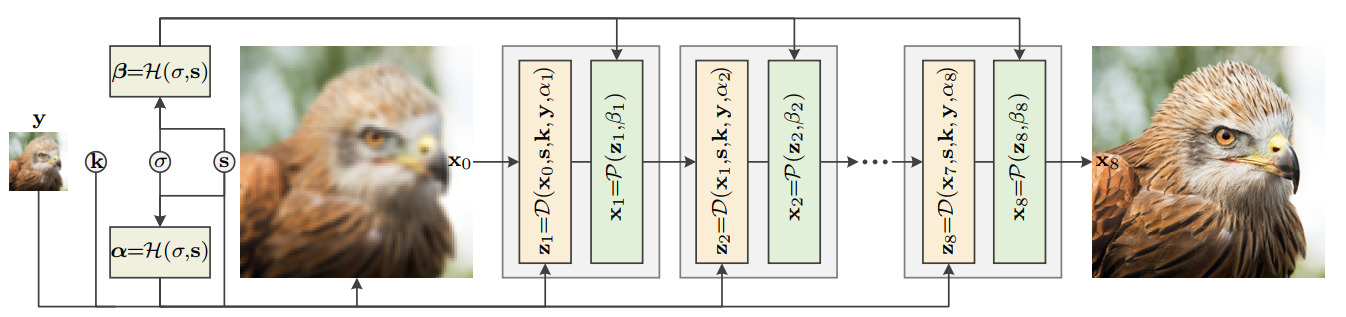
如上图所示，Unfolding SuperResolution Network(USRNet) 主要的输入为低分辨率图 \(y\)，模糊核 \(k\)，噪声水平 \(\sigma\)，以及图像缩放比例 \(s\)。整个模型还有三个模块 \(\mathcal{D}\)、\(\mathcal{P}\) 以及 \(\mathcal{H}\)，分别的功能是进行基于模型的超分、基于学习的去噪以及超参数的预测。整个流程为：
♠ 将预设的噪声水平 \(\sigma\) 与缩放倍数 \(s\) 作为 \(H\) module 的输入，对超参数 \(\alpha\) 和 \(\beta\) 进行预测；
♣ 将 \(y\) 使用简单的上采样到最后的输出 \(x_{last}\) 一样的尺寸，作为迭代最初始的输入 \(x_0\)，最后将 \(x_0,s,k,y,\alpha\) 作为 \(\mathcal{D}\) module 的输入。得到 \(z\) 一次迭代的解；
♥ 将 \(\mathcal{D}\) module 得到的解以及预测的超参数 \(\beta\) 作为输入送入 \(\mathcal{P}\) module 得到一次迭代的 \(x\)；
♦ 最后将得到的 \(x\) 送入下一轮迭代。

Data module H

\(\mathcal{H}\) 模块其实就是将预设的噪声水平和需要超分的倍数作为输入，其实现是深度学习的方式，使用简单的几层网络实现，并预测接下来每一次迭代需要的超参数 \(\alpha_1, \alpha_2, \ldots\)，\(\beta_1, \beta_2, \ldots\)。

Data module D

\(\mathcal{D}\) 模块被称之为数据模块，它的作用实际上是用来实现 (#) 式的第一式的。其实它就是一张图片在一次迭代中的超分后的解析解。式中的前面一项是使用基于模型的方法对图像进行超分辨的重建，这种基于模型的方法可以对任意 scale、任意模糊核进行超分辨重建，后面一项可以看作正则化项，用于 x 与 z 进行逼近。

Prior module P

\(\mathcal{P}\) 模块被称之为先验模块，也就是 (#) 式的第二式。常常这一式被看作去噪的过程，因为噪声可以用先验知识预设，因而被称之为先验项。文章采用基于学习（也就是深度学习）的方法来进行求解得到去噪后的图像 \(x\)。文章使用的结构叫做 ResUNet，顾名思义是将 residual blocks 整合进入了 U-Net，网络结构比较简单，具体可以查看代码。

关于训练

USRNet 关于训练数据的制作，使用随机的高斯核与运动模糊核来作为卷积的模糊核，再经过下采样并添加不同水平的白噪声来制作每张 HR 的 LR，并且每个 batch 从 \(s={1,2,3,4}\) 中选择一个作为下采样的倍数，并且也作为模型关于这个 batch 进行超分 scale 的输入。这样一来使得 USRNet 可以对任意 scale、任意模糊核的情况具有较强的泛化性。

关于 USRNet 的泛化性

虽然 USRNet 是在模糊核为 \(25*25\) 的情况下进行训练的，然而在测试超分 \(67*67\)，\(70*70\) 时，也表现出不错的效果。

一些总结

ZhangKai 这篇文章使用了 HQS 来把优化问题分裂为可迭代的两个子问题，使得基于模型核基于学习进行结合成为了可能。基于模型超分让 USRNet 更加灵活，可以针对不同的模糊核与上采样尺寸的情况进行超分，而基于学习去噪可以不用预定义去噪器，可以尽可能去拟合各种可能情况的噪声。

但是我认为其仍有改进的地方：

♠ 进行实际应用的时候，需要对每张图片指定模糊核，然而这个模糊核的选定是否符合真实情况比较影响后面超分的效果。因此，是否考虑进行设计一个对 kernel 进行预测的网络
♣ 每张图需要指定噪声水平，这一点也没有做到自适应

代码位置