关于自然语言处理的一些知识

To Be Continued~

常见的 NLP 结构

RNN(Recurrent Neural Network)

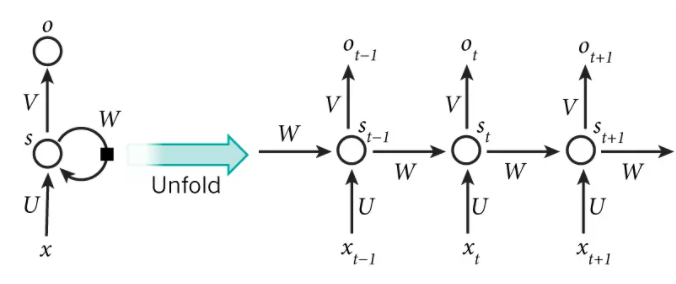
其中 \(x_t\) 是第 \(t\) 阶段（可以是时间上，也可以是空间上）的输入，\(s_t\) 是第 \(t\) 阶段的隐藏状态（有的论文也用 \(h_t\) 表示），\(o_t\) 是第 \(t\) 阶段的输出。那么第 \(t\) 阶段可以由下计算得到：

\[\begin{aligned} s_t &= f(U x_t + W s_{t-1}) \\ o_t &= g(V s_t) \end{aligned} \]

其中 \(W,V,U\) 都是权重。可见 \(t\) 阶段会考虑 \(t-1\) 阶段的隐藏状态 \(s_{t-1}\) 综合 \(t\) 阶段的输入 \(x_t\) 得到 \(t\) 阶段的隐藏状态 \(s_t\) 得到 \(t\) 的输出 \(o_t\)。但是得到 \(s_{t-1}\) 又会用到 \(t-2\) 的隐藏状态 \(s_{t-2}\)，由此迭代（套娃），得到 \(t\) 阶段的隐藏状态 \(s_t\) 会考虑之前所有的隐藏状态，又因为隐藏状态跟输入 \(x\) 有关，因此 \(t\) 阶段的输出 \(o_t\) 综合了之前所有的输入 \((x_{t-1},x_{t-2},x_{t-3}...)\)。

一般 \(f\) 为激活函数 sigmoid 或者 tanh，但是这两个函数的导数都是小于等于 1 的，也就是大多数时候都是小数相乘，这对于较长的序列可能导致后面的梯度消失；同时，由于权重矩阵的累乘，可能会导致梯度爆炸的发生。因此，传统的 RNN 存在长期依赖问题。

LSTM(Long Short-Term Memory)

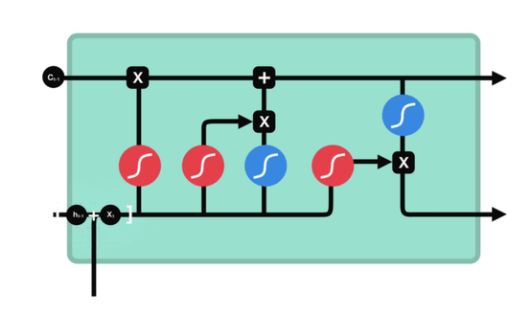
LSTM 通过细胞状态以及各种门结构来解决 RNN 中存在的长期依赖问题。首先 LSTM 存在三种门：遗忘门、输入门、输出门，图中红色是三个门使用 sigmoid 激活函数，旨在将其映射到 0 至 1 之间，越接近 1 表示越需要保留，越接近 0 表示可以丢弃。图中的蓝色则是 tanh 激活函数，× 和 + 表示点乘和点加。

• Forget Gate
  首先将输入 \(x_t\) 和上一阶段的隐藏状态 \(h_{t-1}\) (也是上面提到的 \(s_{t-1}\))进行 concat 后用最左边的 sigmoid 激活得到遗忘门的输出 \(f_t\)（显然 \(f_t\) 在 0 到 1 之间）

\[f_t = \sigma (W_f [h_{t-1},x_t] + b_f) \]

• Input Gate
  同遗忘门一样，将输入和上一阶段的隐藏状态送入输入门（即 中间的sigmoid 函数）得到输入门的输出 \(i_t\)，另一方面送一份进入 tanh 激活函数得到 \(t\) 阶段的初始细胞状态\(\widetilde{c}_{t}\)。

\[\begin{aligned} i_t &= \sigma (W_i [h_{t-1},x_t] + b_i) \\ \widetilde{c}_{t} &= tanh(W_c [h_{t-1},x_t] + b_c) \end{aligned} \]

然后遗忘门的输出 \(f_t\) 与上一阶段的细胞状态 \(c_{t-1}\) 进行点乘，得到的结果表示上一阶段的细胞状态最后保留下来进行下一步计算的值，同样使用输入门的输出与 \(t\) 阶段的初始细胞状态进行点乘，最后将两次点乘的结果相加得到 \(t\) 阶段的细胞状态 \(c_t\)。

\[c_t = f_t \cdot c_{t-1} + i_t \cdot \widetilde{c}_{t} \]

• Output Gate
  同输入门一样，将输入和上一阶段的隐藏状态送入输出门（即 最右边的sigmoid 函数）得到输出门的输出 \(o_t\)，然后再将由上两个门努力得到的 \(t\) 时刻的细胞状态 \(c_t\) 经过蓝色的 tanh 激活函数后与 \(o_t\) 进行点乘，最后得到此阶段的隐藏状态
  \(h_t\)。

\[\begin{aligned} o_t &= \sigma (W_o [h_{t-1},x_t] + b_o) \\ h_t &= o_t \cdot tanh(c_t) \end{aligned} \]

最后将 \(t\) 阶段的细胞状态 \(c_t\)（最上边的分支）和隐藏状态 \(h_t\)（最下边的分支）送入下一阶段。实际上三个门的作用都是通过此阶段的输入和上一阶段的隐藏状态来得到一个权重，这个权重是介于 0 到 1 之间的，然后由对应的权重来决定上一阶段的细胞状态、此阶段的初始细胞状态、此阶段的细胞状态等需要保留的部分，并以此来计算此阶段细胞状态和隐藏状态的值。

BiLSTM

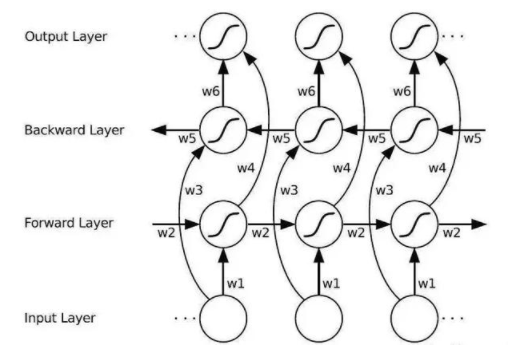
同经典的 RNN 一样，LSTM 同样一个阶段只考虑到了这个阶段之前所有阶段的信息，无法兼并上下文的信息，因此便有的了双向长短时记忆。如图其原理也比较简单，先按顺序正向计算一遍，然后再反向计算一遍，最后将结果进行 concat 后再进行维度的调整就好了。

GRU(Gate Recurrent Unit)

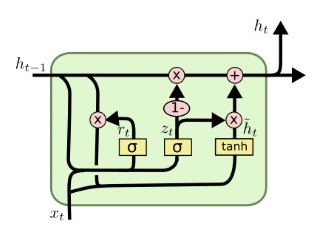
GRU(2014) 比起 LSTM(1997) 晚 17 年提出，同样是为了解决长期依赖和反向传播中的梯度，但是 GRU 的参数更少需要消耗的计算资源也更少，有一篇论文是这么说的：

We choose to use GRU in our experiment since it performs similarly to LSTM but is computationally cheaper.

GRU 同样使用了门的技巧，其中存在两个门：重置门和更新门，也是使用 sigmoid 函数来设计门结构。而且可以发现 GRU 已经没有细胞状态这个东西来传递信息了。

• Reset Gate
  首先将输入 \(x_t\) 和上一阶段的隐藏状态 \(h_{t-1}\) 进行 concat 后，送入重置门（左边的 sigmoid 函数）得到重置门的输出 \(r_t\)。

\[r_t = \sigma(W_r [h_{t-1},x_t] + b_r) \]

然后利用重置门得到的输出对 \(h_{t-1}\) 进行重置（有点 LSTM 遗忘门的意思），再和输入进行 concat 经过 tanh 后得到 \(t\) 阶段的初始隐藏状态 \(\widetilde{h}_{t}\)。

\[\widetilde{h}_{t} = tanh(W [r_t \cdot h_{t-1},x_t] + b) \]

• Update Gate
  同重置门一样，使用输入和上一阶段的隐藏状态通过更新门（右边的 sigmoid 函数）得到更新门的输出 \(u_t\)。

\[u_t = \sigma(W_u [h_{t-1},x_t] + b_u) \]

最后通过更新门的输出来调和上一阶段隐藏状态 \(h_{t-1}\) 和此阶段的初始隐藏状态 \(\widetilde{h}_{t}\) 的比例得出最终的隐藏状态 \(h_t\)。

\[h_t = (1 - u_t) \cdot h_{t-1} + u_t \cdot \widetilde{h}_{t} \]

事实上 GRU 和 LSTM 的门的数量和结构都是可以灵活调整的，有研究者对其进行变异得到了 10000 个新模型，然后在字符串、结构化文档、语言模型以及音频等场景进行试验，最后得到总结如下：

♠ GRU，LSTM 仍是表现最好的模型
♣ GRU 除了在语言模型的场景外其余均超过 LSTM
♥ LSTM 的输出门的偏置的均值初始化为 1 时，性能接近 GRU
♦ LSTM 中门的重要性排序：遗忘门 > 输入门 > 输出门

Transformer

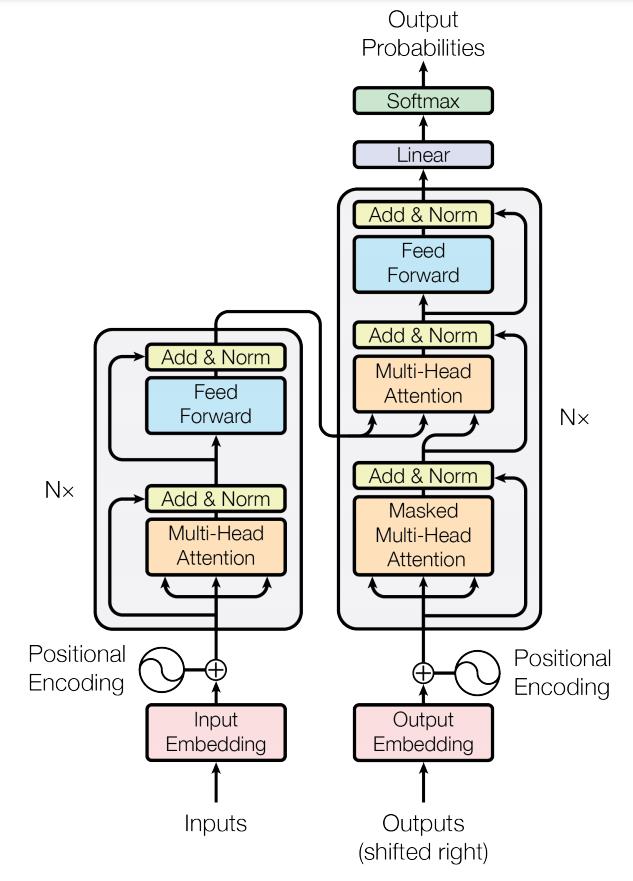
Transformer 是 Google 在 Attention Is All You Need 这篇论文提出的，但是我第一次接触 Transformer 并进行了复现是在 2020 年 Facebook 将其用于目标检测领域使用实现完全端到端的检测，在文章 End-to-End Object Detection with Transformers 中使用 Transformer 对 backbone 提取的视觉特征进行处理搭配二匹配的匈牙利算法在无后处理 nms 的情况下进行预测。之后 Transformer 就由 NLP 跑到 CV 领域遍地开花了。

由上图可以看出，Transformer 主要由几个组件来组成的：多头注意力(Muti-Head Attention)、前向传播层(Feed Forward)、然后就是一些 BN 层。

接下来我分别进行一下介绍，在介绍多头注意力之前，先得介绍一下缩放点积注意力(Scaled Dot-Product Attention)

• Scaled Dot-Product Attention

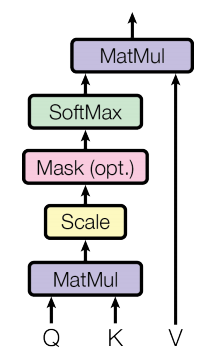
初看这个结构，虽然结构很简单，但依然应该是感觉摸不着头脑的。首先这里的 Q、K、V 是怎么来的？话不多说，请看下图

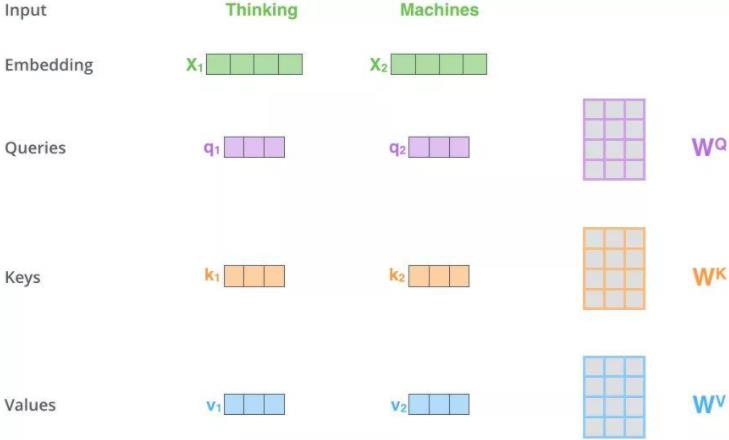
Q、K、V 分别代表的是 Query、Key、Value。借用上图来说明这三者的来历，首先得到输入的 Embedding 向量 \(X_1,X_2\)，然后再和 Q、K、V 对应的权重相乘得到对应的 q、k、v。这里的权重反映在代码里面可以用全连接层来实现。

\[\begin{cases} Q = X \times W_Q \\ K = X \times W_K \\ V = X \times W_V \end{cases} \\ here \ X = [X_1;X_2],Q = [q_1;q_2],K = [k_1;k_2],V = [v_1;v_2] \]

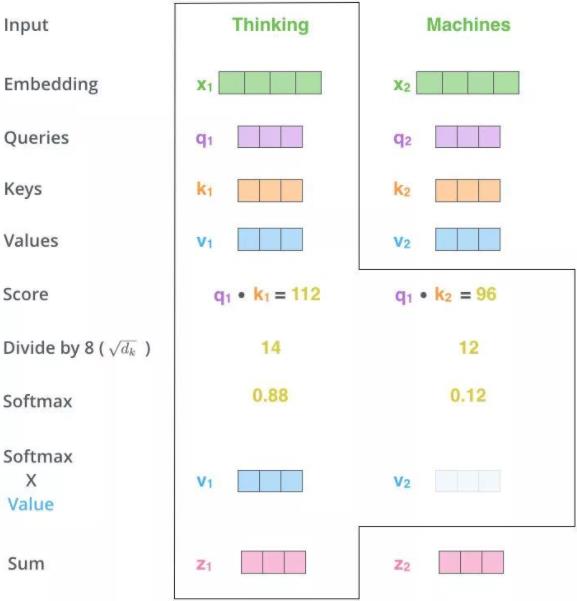
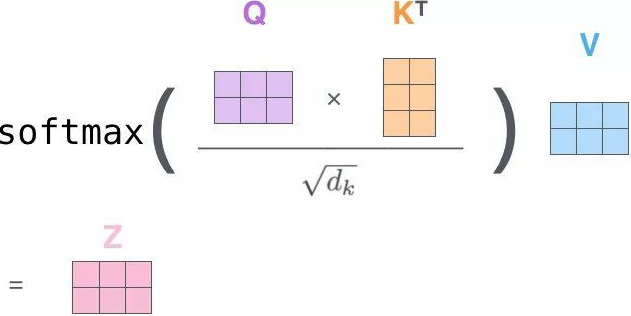
然后再用 Q（询问）去点乘 K（键）得到 score（分数），将得到的分数除以 Q 或者 K 的维度进行放缩，最后进行 softmax 便得到这个输入（单词）对于其他输入（单词）的权重，这个值越大表示两个输入的相关性越大越需要注意，得到的权重分别乘以对应的 V（值）然后再点加得到最后的输出 Z（一般性而言，只看第一行即可）：

\[\begin{aligned} Z &= softmax (\frac{Q \times K^\top}{\sqrt{d_k}}) \times V \\ &= softmax (\frac{[q_1;q_2] \times [k_1;k_2]^\top}{\sqrt{d_k}}) \times [v_1;v_2] \\ &= softmax (\frac{\begin{bmatrix} q_1 k_1 & q_1 k_2 \\ q_2 k_1 & q_2 k_2 \end{bmatrix}}{\sqrt{d_k}}) \times [v_1;v_2] \\ \end{aligned} \]

• Muti-Head Attention

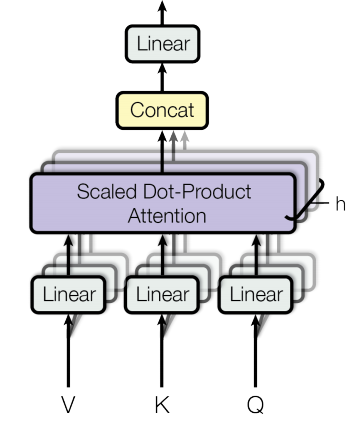
多头注意力事实上就是将得到的 Q、K、V 送入多个并行的缩放点积注意力（多头的体现），最后将结果进行 concat 并通过全连接层进行维度的调整。

• Point wise feed forward network
  点式前馈网络实际上就是全连接层，用于维度的调整。

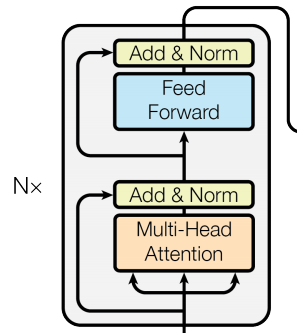
最后，让我们回到第一张图左边的是编码器（encoder），右边的是解码器（decoder）。不过，都基本是上图一样的结构，然后重复多次而组成。将编码器和解码器连接便组成了 Transformer。当然具体细节包括输入部分的位置编码(Positional Encoding)的实现，具体参数的设置等，可以阅读原论文和访问 Tensorflow 官网关于 Transformer 的代码（tf2.0+keras实现），写的很详细啦！

Classical Attention Mechanism

在自然语言处理领域，如 Transformer 的 Encoder 与 Decoder 的结构十分常见，经典的如传统seq2seq模型，然后注意力机制也广泛应用，这里介绍两种应用在seq2seq模型的经典注意力机制，其所用技巧在 Transformer 也是有所体现的。

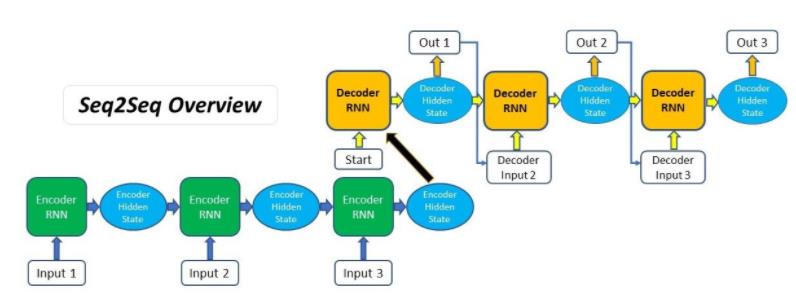
• Bahdanau Attention

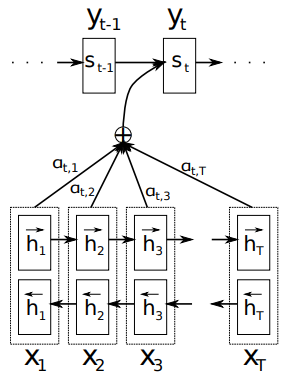
如上图 Bahdanau 等人在一个编码器为双向 RNN 的 seq2seq 结构里加入了注意力机制的计算。所以这里可以联系之前介绍的 RNN 结构，首先编码器输出各个阶段的隐藏状态：

\[h_i = tanh(W_i[h_{i-1},x_i] + b_i) \]

编码器所有阶段的隐藏状态都被用于计算解码器第 \(t\) 阶段的输出，不过第一步是先计算解码器第 \(t\) 阶段关于编码器每个阶段的注意力权重，需要使用的是解码器第 \(t-1\) 阶段的隐藏状态 \(s_{t-1}\) 和编码器第 \(i\) 阶段的隐藏状态 \(h_i\) 进行 concat 后计算，得到编码器第 \(i\) 阶段的隐藏状态 \(h_i\) 对解码器第 \(t\) 阶段的影响程度因子。

\[e_{ti} = v_a^\top tanh (W_a [s_{t-1},h_i]) \]

其中 \(v_a^\top,W_a\) 都是权重矩阵。然后将编码器每个阶段对解码器第 \(t\) 阶段的影响因子进行 softmax 运算归一化后便得到了编码器每个阶段的隐藏状态对应的注意力权重（这里和 Transformer 将 Q 和 K 矩阵相乘后进行 softmax 类似），例如编码器第 \(i\) 阶段对解码器第 \(t\) 阶段的注意力权重:

\[\alpha_{ti} = \frac{exp(e_{ti})}{\sum^T_{k=1} exp(e_{tk})} \]

得到了编码器每个阶段的注意力权重之后，将注意力与对应的编码器的隐藏状态相乘得到解码器第 \(t\) 阶段的语义向量 \(c_t\)。

\[c_t = \sum_{i=1}^T \alpha_{ti} h_i \]

现在就可以利用解码器上一阶段的隐藏状态 \(s_{t-1}\)，上一阶段的输出 \(y_{t-1}\) 以及语义向量 \(c_t\) 来预测第 \(t\) 阶段的输出 \(y_t\)。

\[\begin{aligned} s_t &= tanh(W_s[s_{t-1},y_{t-1},c_t] + b_s) \\ y_t &= softmax(V s_t) \end{aligned} \]

• Luong Attention

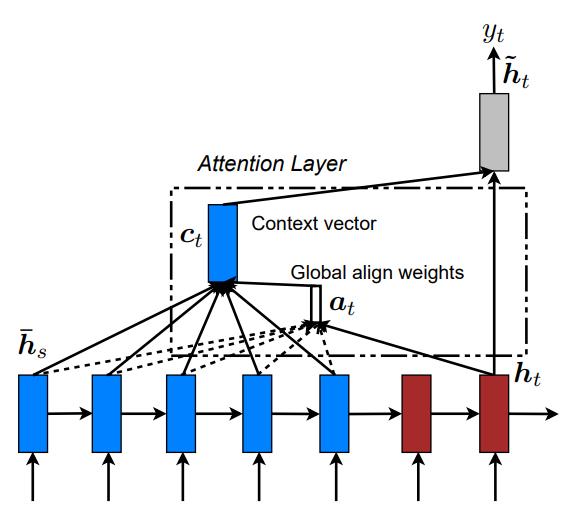
其实 Luong Attention 与 Bahdanau Attention 的过程基本一致，首先想办法分别求得编码器每个阶段对解码器某一阶段的影响程度因子 \(e_{ti}\)，利用 \(e_{ti}\) 得到对应的注意力权重，使用注意力权重与编码器每个阶段的隐藏状态得到解码器那一阶段的语义向量，然后由此来求解码器的一些变量。

Luong Attention 中先通过解码器第 \(t-1\) 阶段的隐藏状态和输出得到第 \(t\) 阶段的隐藏状态。

\[s_t = tanh(W[s_{t-1},y_{t-1}] + b) \]

值得一提的是 Luong Attention 在计算影响程度因子（在论文中也称为 score）进行了多种尝试。

\[e_{ti} = score = \begin{cases} s_t^\top h_i \\ s_t^\top W_a h_i \\ v_a^\top tanh (W_a [s_{t-1},y_{i-1}]) \end{cases} \]

上式第一二种是以乘积的形式，是乘性 attention 机制(Transformer 里面 Q 和 K 矩阵相乘得到的分数也是用的乘性 attention机制），而且第三种也是 Bahdanau Attention 使用的，是加性 attention 机制。然后计算注意力权重 \(\alpha_{ti}\) 和解码器第 \(t\) 阶段的语义向量 \(c_t\) 的方式与 Bahdanau 所用是一致的。然后利用解码器第 \(t\) 阶段的隐藏状态和语义向量注意力层的隐藏状态 \(\widetilde{s}_t\)（这里可以理解为计算了一个中间变量）最后由此得到解码器的输出。

\[\begin{aligned} \widetilde{s}_t &= tanh(W_c[s_t,c_t] + b_c) \\ y_t &= softmax(V\widetilde{s}_t) \end{aligned} \]

Bahdanau Attention 与 Luong Attention 除了在影响程度因子那有所不同以外，值得注意的是 Luong Attention 直接利用的解码器上一阶段的隐藏状态 \(s_{t-1}\) 和输出 \(y_{t-1}\) 来得到本阶段的隐藏状态 \(s_t\)，而且这是在得到语义向量之前，然后计算影响程度因子使用的 \(s_t\) 与解码器各个阶段的隐藏状态得到，而 Bahdanau Attention 是用的 \(s_{t-1}\)。最后得到输出 Luong Attention 采用了使用中间变量 \(\widetilde{s}_t\) 的方式，而 Bahdanau Attention 较为直接。

流程总结如下：

♥ Bahdanau Attention：\(s_{t-1} \rightarrow e_{ti} \rightarrow c_t \rightarrow s_t \rightarrow y_t\)
♦ Luong Attention: \(s_{t-1} \rightarrow s_t \rightarrow e_{ti} \rightarrow c_t \rightarrow \widetilde{s}_t \rightarrow y_t\)

之后出现了很多变种的注意力机制，但基本上都是通过这两种结构在不同地方进行修改的。