Apriori算法-位运算-C语言

原文地址：http://blog.csdn.net/liema2000/article/details/6118423

//////////////////////////////////////////////////////////////////////////
/*
* 文件名称：FAST apriori.cpp

* 摘 要：采用位运算提高算法的效率

* 将每一项抽象为数值，通过与运算判断是否存在，abcde为16,8,4,2,1换成2进制，各占一个位置，互相不干扰。局限于字母。换算的比较字符可以是a-z任意字符。

*/////////////////////////////////////////////////////////////////////////

#include <stdio.h>
#include <string.h>

typedef struct
{
char item[10]; //数据项
int min_supp_count;//最小支持度数
} C_Node; //候选集

typedef struct
{
char item[10]; //数据项
int min_supp_count;//最小支持度数
} L_Node; //频繁集

char D[10][10];
L_Node L[100];
C_Node C[100];
int min_supp_count=2;
int num=100;
void InPut()
{
strcpy(D[1],"abe");
strcpy(D[2],"bd");
strcpy(D[3],"bc");
strcpy(D[4],"abd");
strcpy(D[5],"ac");
strcpy(D[6],"bc");
strcpy(D[7],"ac");
strcpy(D[8],"abce");
strcpy(D[9],"abc");
}//end of InPut

int * DB=new int[num];

void suppDB()
{
int m='e';
int n;
int k;
for (int i=1;i<=9;i++)
{
n=strlen(D[i]);
DB [i]=0;
for (int j=0;j<n;j++)//将每一项生成一个数值，如abe=16+8+1=25，bd=8+2=10
{
k=1;
DB [i]+=k<<(int)(m-D[i][j]);
}
}
}

void check_supp(int num,int no)
{
int i,j,k,m;
int check;
m='e';

for(i=1;i<=num;i++)
{
check=0;
C[i].min_supp_count=0;
for (j=0;j<no;j++)
{
k=1;
check+=(int)(k<<(m-C[i].item[j]));
}
for (j=1;j<=9;j++)
{
if (check==(check&DB[j]))
{
C[i].min_supp_count+=1;//子集存在，支持度数加1
}
}
}

}

void C1()
{
//功能：扫描数据集D生成1项候选集C1
//输入：数据集D
//输出1项候选集C1
//初始条件 数据集D 非空
strcpy(C[1].item,"a");
strcpy(C[2].item,"b");
strcpy(C[3].item,"c");
strcpy(C[4].item,"d");
strcpy(C[5].item,"e");

C[0].min_supp_count=5; //1 项候选集的个数，在本算法中，用C[0].min_supp_count来保存候选集Cn的个数

check_supp(5,1);


} //end of C1()

void Cn( int n)
{
//用频繁集Ln-1为基础，通过连接得到n项候选集Cn

int i,j,k,p,num;
int no=0,temp=0;

C[0].min_supp_count=0; //初始化

num=L[0].min_supp_count; //num是Ln-1项集的数据个数

for(i=1;i<=num;i++)

for(j=i+1;j<=num;j++) //for2
{

temp=1; //测试是否满足联结条件
if(n>2)//if 1
{
for(k=0;k<n-2;k++) //for3
{
if(L[i].item[k]!=L[j].item[k])
{
temp=0;
break;
}//if 1

}//end for3

}//end if1

if(temp==1)//满足联结条件
{
no++;

for(p=0;p<=n-2;p++)
C[no].item[p]=L[i].item[p];
C[no].item[p]=L[j].item[p-1];
C[no].min_supp_count=0;
C[0].min_supp_count+=1;
}//end if2
}//end for2
num=C[0].min_supp_count;
check_supp(num,n);//测试支持度
}//end of Cn()

void Ln(int n)
{
int i,j,k;
j=0;
L[0].min_supp_count=0;

for(i=1;i<=C[0].min_supp_count;i++) //for 1
{
if(C[i].min_supp_count >=min_supp_count)
{
j+=1;
strcpy(L[j].item,C[i].item);
L[j].min_supp_count=C[i].min_supp_count;

} //end if

}//end for1

L[0].min_supp_count=j; //保存数据的个数
printf("频繁项目集L%d如下:\n",n);
k=L[0].min_supp_count;
if(k!=0)
{
for(i=1;i<=k;i++)
{
printf("{");
for(j=0;j<n;j++)
printf(" %c ",L[i].item[j]);
printf("} 支持度:%d\n",L[i].min_supp_count);

}//for

}
else
printf("项目集为空\n");

}//end of Ln(int n)

void main()
{
int n=1;
InPut();
suppDB();
C1();//初始化,生成1项候选集C1
Ln(1);//得到1项频繁集L1
while(L[0].min_supp_count!=0)
{
n+=1;
Cn(n);
Ln(n);
}
}

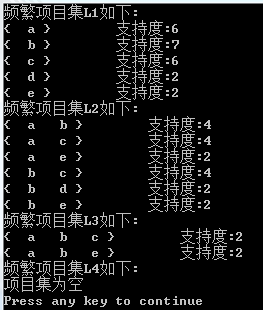
效果图: