矩阵十题（9）

经典题目9 用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案，M<=5，N<2^31，输出答案mod p的结果

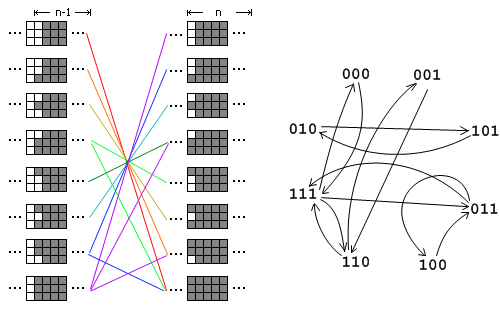
我们以M=3为例进行讲解。假设我们把这个矩形横着放在电脑屏幕上，从右往左一列一列地进行填充。其中前n-2列已经填满了，第n-1列参差不齐。现在我 们要做的事情是把第n-1列也填满，将状态转移到第n列上去。由于第n-1列的状态不一样（有8种不同的状态），因此我们需要分情况进行讨论。在图中，我 把转移前8种不同的状态放在左边，转移后8种不同的状态放在右边，左边的某种状态可以转移到右边的某种状态就在它们之间连一根线。注意为了保证方案不重 复，状态转移时我们不允许在第n-1列竖着放一个多米诺骨牌（例如左边第2种状态不能转移到右边第4种状态），否则这将与另一种转移前的状态重复。把这8 种状态的转移关系画成一个有向图，那么问题就变成了这样：从状态111出发，恰好经过n步回到这个状态有多少种方案。比如，n=2时有3种方 案，111->011->111、111->110->111和111->000->111，这与用多米诺骨牌覆盖 3x2矩形的方案一一对应。这样这个题目就转化为了我们前面的例题8

ps：Matrix67神牛blog上的这一题我也没有找到题目，如果找到了再做做并附上代码，不过初略估计也做不出来，好像很深奥，看不懂神牛是怎么做的

orz Matrix67