矩阵十题(7)
Matrix67原文:经典题目7 VOJ1067
我们可以用上面的方法二分求出任何一个线性递推式的第n项,其对应矩阵的构造方法为:在右上角的(n-1)*(n-1)的小矩阵中的主对角线上填1,矩阵 第n行填对应的系数,其它地方都填0。例如,我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项:
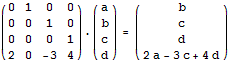
利用矩阵乘法求解线性递推关系的题目我能编出一卡车来。这里给出的例题是系数全为1的情况。
下面是题解
vijos 1067 Warcraft III 守望者的烦恼
题目大意:有n个监狱排成一列,每次最多可以往前走k个监狱,问走到第n个监狱有多少种方案,结果mod 7777777
1<=k<=10, 1<=n<=2^31-1
这道题显然是一道DP,但是数据范围太大了,所以我们要去优化整个DP。
设f[n]为监狱长度为n时的方案数,令f[0]=1
我们从起点出发,每次最多可以走k步,求我们到达点n的方案数f[n],可以分成刚开始走1步,2步,3步....k步的情况,如果刚开始走的是1步,则问题变成走了1步之后,我们从起点出发到达点n-1的方案数f[n-1],
如果刚开始走的是2步,则问题变成走了2步之后,我们从起点出发到达点n-2的方案数f[n-2],
以此类推.....
如果刚开始走的是k步,则问题变成走了k步之后,我们从起点出发到达点n-k的方案数f[n-k],
我们可以发现,这就变成了一个递推的问题了,然后只要我们把走1步,走2步.....走k步后对应的方案数加起来就变成我们要求的f[n]了,
即状态转移方程为:f[n]=f[n-1]+f[n-2]+....f[n-k]。
f[0]=1
当k=1, f[1]=1;
f[2]=f[1]=1;
f[3]=f[2]=1;
f[4]=f[3]=1;
当k=2, f[1]=1;
f[2]=f[1]+f[0]=2;
f[3]=f[2]+f[1]=3;
f[4]=f[3]+f[2]=5;
当k=3, f[1]=1;
f[2]=f[1]+f[0]=2;
f[3]=f[2]+f[1]+f[0]=4;
f[4]=f[3]+f[2]+f[1]=7;
我们手算验证一下发现符合递推式,故推出来的状态转移方程是正确的。
其实任何一个递推式都可以用矩阵乘法来进行优化,我们可以用二分求出任何一个线性递推式的第n项,
其对应矩阵的构造方法为:(和Matrix67的方法有点小不同,此处是Matrix67方法构造的矩阵的转置)
在左下角的(n-1)*(n-1)的小矩阵中的主对角线上填1,矩阵第n列填对应的系数,其它地方都填0。
例如,我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项:
[ [ 0 1 0 0] [f(k-4)] [f(k-3)]
[ 0 0 1 0] * [f(k-3)] = [f(k-2)]
[ 0 0 0 1] [f(k-2)] [f(k-1)]
[ 2 0 -3 4] ] [f(k-1)] [f( k )]
观察一下DP转移方程:F[i]=F[i-1]+F[i-2]+...+F[i-k];注意到这是一个形如f[i]=a1*f[i-1]+a2*f[i-2]+...+ak[i-k];的方程,立刻就反应到可以使用矩阵乘法进行优化。
因此构造一个k*k的矩阵A然后求n-k次幂A^(n-k),然后用递推式构造前k项,然后用之与前面求出的矩阵A^(n-k)相乘得到f[n]即可。
我的构造方法,以k=2为例
[f(1),f(2)] * [ [ 0 1 ] ^(n-k) = [f(n-1),f(n)]
[ 1 1 ] ]
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 11 4 #define M 7777777 5 struct Matrix 6 { 7 __int64 a[N][N]; 8 }res,tmp,origin,A,ans; 9 int n,m,f[N]; 10 Matrix mul(Matrix x,Matrix y) 11 { 12 int i,j,k; 13 memset(tmp.a,0,sizeof(tmp.a)); 14 for(i=1;i<=n;i++) 15 for(j=1;j<=n;j++) 16 for(k=1;k<=n;k++) 17 { 18 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j])%M; 19 tmp.a[i][j]%=M; 20 } 21 return tmp; 22 } 23 void quickpow(int k) //矩阵快速幂 24 { 25 int i; 26 memset(res.a,0,sizeof(res.a)); 27 for(i=1;i<=n;i++) 28 res.a[i][i]=1; 29 while(k) 30 { 31 if(k&1) 32 res=mul(res,A); 33 A=mul(A,A); 34 k>>=1; 35 } 36 } 37 int main() 38 { 39 int k,i,j; 40 while(scanf("%d%d",&k,&m)!=EOF) 41 { 42 memset(f,0,sizeof(f)); 43 f[0]=1; 44 for(i=1;i<=k;i++) //构造前k项 45 for(j=0;j<i;j++) 46 f[i]+=f[j]; 47 memset(A.a,0,sizeof(A.a)); 48 for(i=2;i<=k;i++) //构造矩阵A 49 A.a[i][i-1]=1; 50 for(i=1;i<=k;i++) 51 A.a[i][k]=1; 52 n=k; 53 quickpow(m-k); //A^(n-k) 54 memset(origin.a,0,sizeof(origin.a)); 55 for(i=1;i<=k;i++) //前k项的矩阵[f(1),f(2),f(3)....f(k)] 56 origin.a[1][i]=f[i]; 57 ans=mul(origin,res); //[f(1),f(2),f(3)....f(k)] * A^(n-k) 58 printf("%d\n",ans.a[1][n]%M); 59 } 60 return 0; 61 }
hdu 1757 A Simple Math Problem
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1757
If x < 10 ,则 f(x) = x.
If x >= 10 ,则 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
给出k,m和a0~a9,求f(k)%m, k<2*10^9 , m < 10^5
这是一个递推式,故可以用矩阵乘法来求
根据上面讲的方法构建矩阵A,然后二分求A^(k-10),然后用前k项的矩阵与之相乘即可得到f[n]
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 15 4 struct Matrix 5 { 6 __int64 a[N][N]; 7 }ans,tmp,res,origin,A; 8 int n,m,f[N],a[N]; 9 Matrix mul(Matrix x,Matrix y) 10 { 11 int i,j,k; 12 memset(tmp.a,0,sizeof(tmp.a)); 13 for(i=1;i<=n;i++) 14 for(j=1;j<=n;j++) 15 for(k=1;k<=n;k++) 16 { 17 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j])%m; 18 tmp.a[i][j]%=m; 19 } 20 return tmp; 21 } 22 Matrix quickpow(int k) //矩阵快速幂 23 { 24 int i; 25 memset(res.a,0,sizeof(res.a)); 26 for(i=1;i<=n;i++) 27 res.a[i][i]=1; 28 while(k) 29 { 30 if(k&1) 31 res=mul(res,A); 32 A=mul(A,A); 33 k>>=1; 34 } 35 return res; 36 } 37 int main() 38 { 39 int k,i; 40 while(scanf("%d%d",&k,&m)!=EOF) 41 { 42 n=10; 43 for(i=0;i<n;i++) 44 scanf("%d",&a[i]); 45 f[n]=0; 46 for(i=0;i<n;i++) //求前10项 47 f[i]=i; 48 for(i=0;i<n;i++) 49 f[n]+=a[i]*f[n-1-i]; 50 if(k<=n) 51 printf("%d\n",f[k]); 52 else 53 { 54 memset(A.a,0,sizeof(A.a)); 55 for(i=2;i<=n;i++) //构造矩阵A 56 A.a[i][i-1]=1; 57 for(i=1;i<=n;i++) 58 A.a[i][n]=a[n-i]; 59 res=quickpow(k-10); //A^(k-10) 60 memset(origin.a,0,sizeof(origin.a)); 61 for(i=1;i<=n;i++) //前10项的矩阵[f(1),f(2),f(3)....f(10)] 62 origin.a[1][i]=f[i]; 63 ans=mul(origin,res); //[f(1),f(2),f(3)....f(10)] * A^(n-10) 64 printf("%d\n",ans.a[1][n]%m); 65 } 66 } 67 return 0; 68 }
posted on 2013-05-22 01:15 jumpingfrog0 阅读(496) 评论(0) 编辑 收藏 举报




