矩阵十题（6）

经典题目6

poj   3070   Fibonacci

题目链接：http://poj.org/problem?id=3070

给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31
根据前面的 一些思路，现在我们需要构造一个2 x 2的矩阵，使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵，这两个数就会多迭代一次。那么，我们把这个2 x 2的矩阵自乘n次，再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想，这个2 x 2的矩阵很容易构造出来：

代码如下：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #define N 10
 4 struct Matrix
 5 {
 6     int a[N][N];
 7 }origin,res,tmp,ans;
 8 int n,m;
 9 Matrix mul(Matrix x,Matrix y)
10 {
11     int i,j,k;
12     memset(tmp.a,0,sizeof(tmp.a));
13     for(i=1;i<=n;i++)
14         for(j=1;j<=n;j++)
15             for(k=1;k<=n;k++)
16             {
17                 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j])%m;
18                 tmp.a[i][j]%=m;
19             }
20     return tmp;
21 }
22 void quickpow(int k)  //矩阵快速幂
23 {
24     int i;
25     memset(res.a,0,sizeof(res.a));
26     for(i=1;i<=n;i++)
27         res.a[i][i]=1;
28     while(k)
29     {
30         if(k&1)
31             res=mul(res,origin);
32         origin=mul(origin,origin);
33         k>>=1;
34     }
35 }
36 int main()
37 {
38     int k;
39     n=2;
40     m=10000;
41     while(scanf("%d",&k)&&k!=-1)
42     {
43         origin.a[1][1]=0;  //初始化矩阵A
44         origin.a[1][2]=1;
45         origin.a[2][1]=1;
46         origin.a[2][2]=1;
47         quickpow(k);
48         memset(tmp.a,0,sizeof(tmp.a));   //相当于| 0 |
49         tmp.a[2][1]=1;                   //      | 1 |
50         ans=mul(res,tmp);   
51     /*    for(int i=1;i<=n;i++)
52         {
53             for(int j=1;j<=n;j++)
54                 printf("%d ",res.a[i][j]);
55             printf("\n");
56         }*/
57         printf("%d\n",ans.a[1][1]%m);
58     }
59     return 0;
60 }
View Code


此外，根据题目的描述，也可以不用构造矩阵

由于斐波那契数列满足

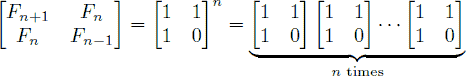
故只需求矩阵 A = 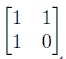的n次幂mod 10000，结果保存在res.a中，然后输出res.a[1][2]mod 10000即可

直接矩阵快速幂就行了。

代码如下：

 1 #include<stdio.h>
 2  #include<string.h>
 3  #define N 10
 4  struct Matrix
 5  {
 6      int a[N][N];
 7  }origin,res,tmp;
 8  int n,m;
 9  Matrix mul(Matrix x,Matrix y)
10  {
11      int i,j,k;
12      memset(tmp.a,0,sizeof(tmp.a));
13      for(i=1;i<=n;i++)
14          for(j=1;j<=n;j++)
15              for(k=1;k<=n;k++)
16              {
17                  tmp.a[i][j]+=(x.a[i][k]*y.a[k][j])%m;
18                  tmp.a[i][j]%=m;
19              }
20      return tmp;
21  }
22  void quickpow(int k)  //矩阵快速幂
23  {
24      int i;
25      memset(res.a,0,sizeof(res.a));
26      for(i=1;i<=n;i++)
27          res.a[i][i]=1;
28      while(k)
29      {
30          if(k&1)
31              res=mul(res,origin);
32          origin=mul(origin,origin);
33          k>>=1;
34      }
35  }
36  int main()
37  {
38      int k;
39      n=2;
40      m=10000;
41      while(scanf("%d",&k)&&k!=-1)
42      {
43          origin.a[1][1]=1;  //初始化矩阵A
44          origin.a[1][2]=1;
45          origin.a[2][1]=1;
46          origin.a[2][2]=0;
47          quickpow(k);
48          printf("%d\n",res.a[1][2]%m);
49      }
50      return 0;
51  }
View Code

 

 

posted on 2013-05-21 00:49  jumpingfrog0  阅读(383)  评论(0)  编辑  收藏  举报

导航