矩阵十题(3)
经典题目3
POJ3233
题目大意:给定矩阵A,求A + A^2 + A^3 + ... + A^k的结果(两个矩阵相加就是对应位置分别相加)。输出的数据mod m。k<=10^9。
这道题两次二分,相当经典。首先我们知道,A^i可以二分求出。然后我们需要对整个题目的数据规模k进行二分。比如,当k=6时,有:
A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3) + A^3*(A + A^2 + A^3)
应用这个式子后,规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3,即可得到原问题的答案。
奇数: F[n]=F[n-1]+A^n
偶数: F[n]=F[n/2]+F[n/2]*An/2
算法: 二分+矩阵快速幂
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 31 4 struct Matrix 5 { 6 int a[N][N]; 7 }res,origin,tmp,A,B,C,ans; 8 int n,m; 9 Matrix mul(Matrix x,Matrix y) //矩阵乘法 10 { 11 int i,j,k; 12 memset(tmp.a,0,sizeof(tmp.a)); 13 for(i=1;i<=n;i++) 14 for(j=1;j<=n;j++) 15 for(k=1;k<=n;k++) 16 { 17 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j]); 18 tmp.a[i][j]%=m; 19 } 20 return tmp; 21 } 22 Matrix quickpow(Matrix origin,int k) //矩阵快速幂 23 { 24 int i; 25 memset(res.a,0,sizeof(res.a)); 26 for(i=1;i<=n;i++) 27 res.a[i][i]=1; 28 while(k) 29 { 30 if(k&1) 31 res=mul(res,origin); 32 origin=mul(origin,origin); 33 k>>=1; 34 } 35 return res; 36 } 37 Matrix sum(Matrix x,Matrix y) //矩阵求和 38 { 39 int i,j; 40 for(i=1;i<=n;i++) 41 for(j=1;j<=n;j++) 42 tmp.a[i][j]=(x.a[i][j]+y.a[i][j])%m; 43 return tmp; 44 } 45 Matrix bin(int k) 46 { 47 if(k<=1) 48 return A; 49 else if(k%2) //奇数:F[n]=F[n-1]+A^n 50 { 51 B=bin(k-1); 52 C=quickpow(A,k); 53 return sum(B,C); 54 } 55 else //偶数: F[n]=F[n/2]+F[n/2]*A^(n/2) 56 { 57 B=bin(k/2); 58 C=quickpow(A,k/2); 59 C=mul(C,B); 60 return sum(B,C); 61 } 62 } 63 int main() 64 { 65 int i,j,k; 66 scanf("%d%d%d",&n,&k,&m); 67 for(i=1;i<=n;i++) 68 for(j=1;j<=n;j++) 69 scanf("%d",&A.a[i][j]); 70 ans=bin(k); //二分 71 for(i=1;i<=n;i++) 72 { 73 for(j=1;j<=n;j++) 74 if(j<n) 75 printf("%d ",ans.a[i][j]); 76 else 77 printf("%d\n",ans.a[i][j]); 78 } 79 return 0; 80 }
hdu 1588 Gauss Fibonacci
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1588
题目大意:求下标为g(x)=k*i+b,(i=0,1,…,n-1)的Fibonacci数列F( g(i) )的和mod m,即求Fib(k*0+b)+Fib(k*1+b)+Fib(k*2+b)+......+Fib(k*(n-1)+b) mod m
这题和poj 的3233 类似
Fibonacci数列有一种特殊的解法,即

所以只需要令矩阵A=
sum=A^(k*0+b) + A^(k*1+b) + … + A^(k*(n-1)+b)
=A^b*[A^(k*0) + A^(k*1) + … + A^(k*(n-1))]
=A^b*[(A^k)^0 + (A^k)^1 + … + (A^k)^(n-1)]
我们可以二分分别求出A^b 和 A^k。再把A^k看成整体,再用二分求解中括号内的等比数列的和。
设F(n)=(A^k)^0 + (A^k)^1 + … + (A^k)^(n-1) + (A^k)^n ,其中S0=(A^k)^0=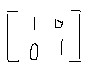
奇数:F(n)=S0+F(n-1)+(A^k)^n
偶数:F(n)=S0+F(n/2)+F(n/2)+(A^k)^(n/2)
因为i从0到n-1,所以我们只需计算F(n-1)即可
注意:题目要用到int64
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 2 4 struct Matrix 5 { 6 __int64 a[N][N]; 7 }res,tmp,ans,B,C,S,AB,AK; 8 Matrix A={1,1,1,0}; //初始化矩阵A 9 Matrix S0={1,0,0,1}; //(A^k)^0 10 int m; 11 Matrix mul(Matrix x,Matrix y) //矩阵乘法 12 { 13 memset(tmp.a,0,sizeof(tmp.a)); 14 int i,j,k; 15 for(i=0;i<2;i++) 16 for(j=0;j<2;j++) 17 for(k=0;k<2;k++) 18 { 19 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j]); 20 tmp.a[i][j]%=m; 21 } 22 return tmp; 23 } 24 Matrix quickpow(Matrix origin,int k) //矩阵快速幂 25 { 26 int i; 27 memset(res.a,0,sizeof(res.a)); 28 for(i=0;i<2;i++) 29 res.a[i][i]=1; 30 while(k) 31 { 32 if(k&1) 33 res=mul(res,origin); 34 origin=mul(origin,origin); 35 k>>=1; 36 } 37 return res; 38 } 39 Matrix sum(Matrix x,Matrix y) //矩阵加法 40 { 41 int i,j; 42 for(i=0;i<2;i++) 43 for(j=0;j<2;j++) 44 tmp.a[i][j]=(x.a[i][j]+y.a[i][j])%m; 45 return tmp; 46 } 47 Matrix bin(int n) //二分 48 { 49 if(n<=1) 50 return AK; 51 else if(n%2) 52 { 53 B=bin(n-1); 54 C=quickpow(AK,n); 55 return sum(B,C); 56 } 57 else 58 { 59 B=bin(n/2); 60 C=quickpow(AK,n/2); 61 C=mul(B,C); 62 return sum(B,C); 63 } 64 } 65 void print(Matrix x) 66 { 67 int i,j; 68 for(i=0;i<2;i++) 69 { 70 for(j=0;j<2;j++) 71 printf("%d ",x.a[i][j]); 72 printf("\n"); 73 } 74 } 75 int main() 76 { 77 int k,b,n; 78 while(scanf("%d%d%d%d",&k,&b,&n,&m)!=EOF) 79 { 80 //fibonacci数列满足 |F(n+1) F(n) |= |1 1|^n 81 // |F(n) F(n-1)| |1 0| 82 83 AB=quickpow(A,b); //A^b 84 // print(AB); 85 AK=quickpow(A,k); //A^k 86 // print(AK); 87 S=bin(n-1); //F(n-1) 88 S=sum(S0,S); 89 // print(S); 90 ans=mul(AB,S); 91 printf("%d\n",ans.a[0][1]); 92 } 93 return 0; 94 }
hdu 3306 Another kind of Fibonacci
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3306
题目大意:A(0) = 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2);给定三个值N,X,Y求S(N):S(N) = A(0)2 +A(1)2+……+A(n)2。
这道题目的构造的矩阵比较难想到,要真正意义上理解怎么构造矩阵求解多项式才能比较容易的解出题目,
矩阵构造的方法可以参考我整理的另一篇文章:矩阵构造方法http://www.cnblogs.com/frog112111/archive/2013/05/19/3087648.html
解:
考虑1*4 的矩阵【s[n-2],a[n-1]^2,a[n-2]^2,a[n-1]*a[n-2]】
我们需要找到一个4×4的矩阵A,使得它乘以A得到1×4的矩阵
【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】
即:【s[n-2],a[n-1]^2,a[n-2]^2,a[n-1]*a[n-2]】* A = 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】
= 【s[n-2]+a[n-1]^2 , x^2 * a[n-1]^2 + y^2 * a[n-2]^2 + 2*x*y*a[n-1]*a[n-2] ,
a[n-1]^2 , x*a[n-1]^2 + y*a[n-2]a[n-1]】
可以构造矩阵A为:
1 0 0 0
1 x^2 1 x
0 y^2 0 0
0 2xy 0 y
故:【S[0],a[1]^2,a[0]^2,a[1]*a[0]】 * A^(n-1) = 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】
所以:【S[0],a[1]^2,a[0]^2,a[1]*a[0]】 * A^(n) = 【s[n],a[n+1]^2,a[n]^2,a[n+1]*a[n]】
若A = (B * C ) 则AT = ( B * C )T = CT * BT
故
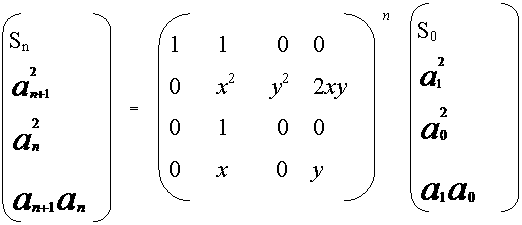
注意:这道题目在hdu上用G++提交的话,用了int64就一直TLE,不用int64就能AC,200+ms
如果用了int64,用C++提交的话,也能AC,800+ms
代码如下:

1 #include<stdio.h> 2 #include<string.h> 3 #define N 4 4 #define M 10007 5 struct Matrix 6 { 7 __int64 a[N][N]; 8 }res,tmp,ans,origin; 9 Matrix A={1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0}; //相当于那个1*4的矩阵的转置,即[s0,a1^2,a0^2,a1*a0]T 10 Matrix mul(Matrix x,Matrix y) 11 { 12 int i,j,k; 13 memset(tmp.a,0,sizeof(tmp.a)); 14 for(i=0;i<4;i++) 15 for(j=0;j<4;j++) 16 for(k=0;k<4;k++) 17 { 18 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j])%M; 19 tmp.a[i][j]%=M; 20 } 21 return tmp; 22 } 23 Matrix quickpow(int k) 24 { 25 int i; 26 memset(res.a,0,sizeof(res.a)); 27 for(i=0;i<4;i++) 28 res.a[i][i]=1; 29 while(k) 30 { 31 if(k&1) 32 res=mul(res,origin); 33 origin=mul(origin,origin); 34 k>>=1; 35 } 36 return res; 37 } 38 int main() 39 { 40 int n,x,y; 41 while(scanf("%d%d%d",&n,&x,&y)!=EOF) 42 { 43 x%=M; 44 y%=M; 45 memset(origin.a,0,sizeof(origin.a)); 46 origin.a[0][0]=origin.a[0][1]=origin.a[2][1]=1; 47 origin.a[1][1]=(x*x)%M; 48 origin.a[1][2]=(y*y)%M; 49 origin.a[1][3]=(2*x*y)%M; 50 origin.a[3][1]=x; 51 origin.a[3][3]=y; 52 res=quickpow(n); //求构造出的矩阵A^n 53 ans=mul(res,A); //A^n * [s0,a1^2,a0^2,a1*a0]T 54 printf("%I64d\n",ans.a[0][0]%M); 55 } 56 return 0; 57 }
posted on 2013-05-16 18:51 jumpingfrog0 阅读(2370) 评论(1) 编辑 收藏 举报





