Longest Palindromic Substring

http://www.felix021.com/blog/read.php?2040

下面以字符串12212321为例，经过上一步，变成了 S[] = "$#1#2#2#1#2#3#2#1#";

然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]），比如S和P的对应关系：

S  #  1  #  2  #  2  #  1  #  2  #  3  #  2  #  1  #
P  1  2  1  2  5  2  1  4  1  2  1  6  1  2  1  2  1
(p.s. 可以看出，P[i]-1正好是原字符串中回文串的总长度）

那么怎么计算P[i]呢？该算法增加两个辅助变量（其实一个就够了，两个更清晰）id和mx，其中id表示最大回文子串中心的位置，mx则为id+P[id]，也就是最大回文子串的边界。

然后可以得到一个非常神奇的结论，这个算法的关键点就在这里了：如果mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i)。就是这个串卡了我非常久。实际上如果把它写得复杂一点，理解起来会简单很多：

//记j = 2 * id - i，也就是说 j 是 i 关于 id 的对称点。
if (mx - i > P[j]) 
    P[i] = P[j];
else /* P[j] >= mx - i */
    P[i] = mx - i; // P[i] >= mx - i，取最小值，之后再匹配更新。

当然光看代码还是不够清晰，还是借助图来理解比较容易。

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。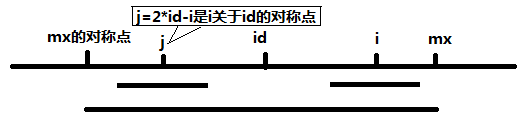


当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。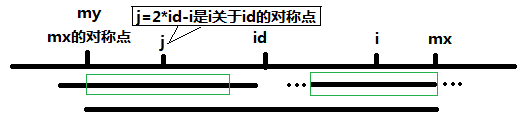


对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

于是代码如下：

//输入，并处理得到字符串s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
    p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
    while (s[i + p[i]] == s[i - p[i]]) p[i]++;
    if (i + p[i] > mx) {
        mx = i + p[i];
        id = i;
    }
}
//找出p[i]中最大的

OVER.

http://blog.csdn.net/hopeztm/article/details/7932245

public class Solution {
    public String longestPalindrome(String s)
    {
        if(s==null||s.length()==0)
            return s;
        StringBuilder sb=new StringBuilder();
        sb.append("$#");
        for(char ch:s.toCharArray())
        {
            sb.append(ch);
            sb.append('#');
        }
        sb.append('!');
        String T=sb.toString();
        int []p=new int[T.length()];
        int mx=0,id=0;
        for(int i=1;i<T.length()-1;i++)
        {
            int j=2*id-i;
            p[i]=mx>i?Math.min(mx-i,p[j]):0;
            while(T.charAt(i+1+p[i])==T.charAt(i-1-p[i]))
                p[i]++;
            if(i+p[i]>mx)
            {
                id=i;
                mx=i+p[i];
            }
        }
        int maxLen=0;
        int centerIndex=0;
        for(int i=1;i<T.length();i++)
            if(p[i]>maxLen)
            {
                maxLen=p[i];
                centerIndex=i;
            }
        return s.substring((centerIndex-1-maxLen)/2,(centerIndex-1-maxLen)/2+maxLen);
    }
}