最长回文子串（Manacher算法）

枚举中心位置法：

//枚举中心位置法
#include<iostream>
#include<string.h>
using namespace std;

const int MAXN = 1e5;

int LongestPalindrome(char *s, int len)
{
    int i, j;
    if (s == NULL || len < 1)
        return 0;
    int max = 0;
    int c;
    for (i = 0; i < len; i++) //枚举中心位置
    {
        for (j = 0; (i - j >= 0) && (i + j < len); j++)   //长度为奇数的情况
        {
            if (s[i - j] != s[i + j])
                break;
            c = j * 2 + 1;
        }
        if (c > max)    //更新max
            max = c;
        for (j = 0; (i - j >= 0) && (i + j + 1 < len); ++j)   //长度为偶数的情况
        {
            if (s[i - j] != s[i + j + 1])
                break;
            c = j * 2 + 2;
        }
        if (c > max)
            max = c;
    }
    return max;
}
int main()
{
    char s[MAXN];
    while(cin >> s)
    {
        cout << LongestPalindrome(s, strlen(s)) << endl;
    }
    return 0;
}

 枚举中心位置中，我们需要特别考虑字符串的长度是奇数还是偶数，所以导致我们在编写代码实现的时候要把奇数和偶数的情况分开编写，而Manacher算法则不用分奇偶来讨论

而且上面这种枚举中心位置往两边找的算法时间复杂度是O(n²)，下面介绍的“马拉车”算法时间复杂度是O(n)

Manacher算法：

　　普通的枚举中心位置的算法需要区分考虑字符串的长度的奇偶性，而Manacher算法则不用区分长度奇偶问题，它的做法是在字符的两边插入一个特殊字符，比如abab转换成#a#b#a#b#，aba转换成了#a#b#a#。为了避免数组越界的问题，还可以在字符串的两端加入特殊的符号。

　　Manacher算法使用了一个辅助数组，暂且叫它 P [ ] ，代表的是以 s [ i ] 为中心的最长回文子串往一个方向的拓展长度（这里让它包括 s [ i ] 本身）

　　S  #  a  #  b  #  b  #  a  #  b  #  c  #  b  #  a  #
　　P  1  2  1  2  5  2  1  4  1  2  1  6  1  2  1  2  1

　　观察一下，发现最大的 p [ ] 值减1正好等于原字符串的最长回文子串的长度，所以要知道最长回文子串的长度只需要把 p [ ] 计算出就行了。所以接下来讨论怎么计算p数组

　　要计算p数组，先引入几个参数的概念，id：表示目前已知的最长回文子串的中心位置下标；mx：mx = id + p [ id ] ，表示这个回文子串的右边界（即这个回文子串的最右元素的下一位）

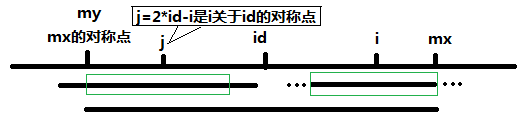
　　然后核心部分是：如果mx > i，那么P [ i ]  >= min(P [ 2 * id - i ], mx - i)。不理解的话再看看下面两张图就懂了，具体实现看下面代码

 

 

#include<iostream>
#include<string>
#include<cstring>
using namespace std;

const int maxn = 1e5 + 10;
string s;
string new_s;
int p[maxn];

string pre(string s)    //初始字符的转换
{
    int len = s.length();
    string ret = "$";    //下标0是$，防止数组越界
    for(int i = 0; i < len; i++)
    {
        ret += "#" + s.substr(i, 1);
    }
    ret += "#@";    //最后加一个符号，防止数组越界
    return ret;
}

int Manacher()
{
    new_s = pre(s);
    int len = new_s.length();
    int max_len = -1;    //最长回文子串的长度
    int id, mx = 0;
    //算法核心
    for(int i = 1; i < len; i++)
    {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while(new_s[i + p[i]] == new_s[i - p[i]])
            p[i]++;
        if(i + p[i] > mx)    //尽可能让mx靠右
        {
            mx = i + p[i];
            id = i;
        }
        max_len = max(max_len, p[i] - 1);
    }

    return max_len;
}
int main()
{
    while(cin >> s)
    {
        cout << "s = " << s << endl;
        cout << "new_s = " << pre(s) << endl;
        cout << "max_len = " << Manacher() << endl;
    }
    return 0;
}

 Reference：

https://segmentfault.com/a/1190000008484167

https://www.felix021.com/blog/read.php?2040