背包问题

0-1背包

问题描述：

　　有n个重量和价值分别是w_i，v_i的物品，从这些物品中挑选出总重量不超过W的物品，求所有方案中价值总和的最大值

分析：

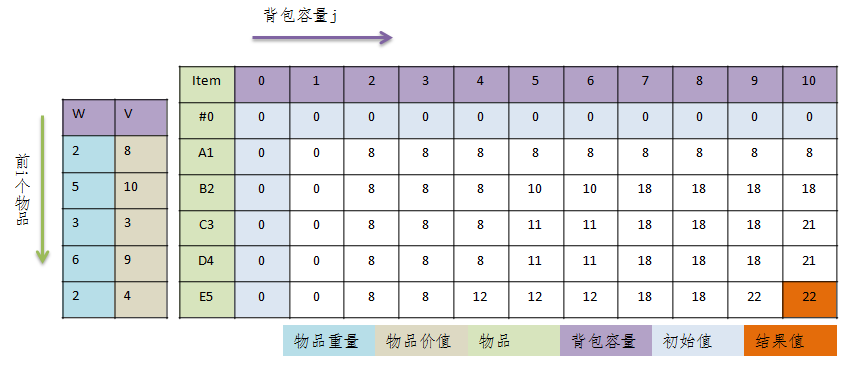
　　dp[ i ][ j ] 表示在前 i 个物品中能装入容量为 j 的背包的最大价值，则有：

　　dp[i][j] = dp[i - 1][j]    j < wi
　　dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - wi] + vi)    j >= wi

　　当前背包容量不允许装入第 i 件物品时，前 i 件和前 i-1 件一样，允许装入时，从两种选择（装、不装）中挑选价值最大的

优化及拓展：

　　在计算 dp[i][j] 时只使用了 dp[i-1][0……j] ，在存储子问题解的时候，只用存储 dp[i-1] 的子问题解即可，所以可以使用滚动数组进行空间优化，用一维数组代替二维，只不过一维的数组，一个是代表正在解决的问题（左边的是 i ），一个是代表子问题（右边的是 i - 1）。即状态转移方程可以这样表示：dp[j] = max(dp[j], dp[j - w[i]] + v[i]); 

　　注意点：若使用滚动数组优化成一维，则 j 的遍历，即背包容量的枚举需要逆序枚举，因为一维数组正序计算时存在值的覆盖（i-1时刻的值会被当前 i 时刻的值覆盖），会使得结果错误。而二维数组标明了是 i 时刻的值还是 i-1 时刻的值，所以正序逆序都无所谓

 

完全背包

 问题描述：

　　在0-1背包的基础上，每种物品可以取任意个

分析：

　　完全背包问题的dp思想可以在0-1背包的基础上改进，增加一个描述选取物品数量的参数，这样的话还需要枚举数量参数的可取值，效率不高

for(int i = 1; i <= n; i++)
{
    for(int j = 1; j <= w; j++)
    {
        for(int k = 0; k * w[i] <= j; k++)
        {
            if(w[i] <= j)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w[i]] + k * v[i]);
            else
                dp[i][j] = dp[i - 1][j];
        }
    }
}

　　虽然在这基础上可以再进行一系列的优化，比如有两种物品，其中一种价值小且重量大，那么就可以把这种物品删除不考虑等等，但是在随机数据中，这种优化效果并不显著，现更换一种dp思路，将完全背包问题转化成0-1背包来解决。

　　上面这种k参数的方法是以每一种物品为单位来枚举每种取多少个来解决的，而现在以每一个物品为单位来看问题，考虑是否在物品总数中添加当前该物品，来看递推式

　　f [ i ] [ j ] = max( f[ i - 1 ] [ j ] , f [ i ] [ j - c[i] ] + w [ i ] )

　　为什么会是f[i][j-c[i]]+w[i]，因为你放第i种物品，并不牵扯到第i-1种物品

for (int i = 1; i <= n; ++i)
{
    for (int j = 1; j <= v; ++j)
    {
        if (c[i] <= j)
            f[i][j] = max(f[i - 1][j], f[i][j - c[i]] + v[i]);
        else
            f[i][j] = f[i - 1][j];
    }
}

优化及拓展：

　　空间优化一下，和0-1背包问题不同的是，0-1背包空间优化后遍历顺序是逆序，而这里完全背包问题则是需要顺序。

　　考虑一下原因，在未考虑第 i 种物品的时候，前面的 i - 1 种物品存在一个最优解，当考虑第 i 种物品的添加时，可能最优解会更新，所以需要顺序来覆盖更新最优解

for (int i = 1; i <= n; ++i)
{
    for (int j = w[i]; j <= v; ++j)
    {
        f[j] = max(f[j], f[j - c[i]] + v[i]);
    }
}

 

参考博客：

http://www.cnblogs.com/Kalix/p/7617856.html

https://www.cnblogs.com/Kalix/p/7622102.html