最优三角剖分

问题描述：

　　给一个有n个顶点的凸多边形，有很多方法进行三角剖分(polygon triangulation) 。给每个三角形规定一个权函数w(i,j,k)（比如三角形的周长或者三顶点的权和或者三角形的面积等等），求让所有三角形权和最大的方案。

 

分析：

　　这个问题的关键在于状态的定义，因为如果允许随意切割，显然任意“半成品” 多边形的各个顶点可以是原多边形中随意选取的，很难简洁的定义成状态。但我们又可以发现，对于同一种切割方法，我们可以有多种切割顺序，但切割方法就已经决定了这个方法产生的结果，我们只要计算其中一种切割顺序就好了，所以不如把决策顺序规范化。

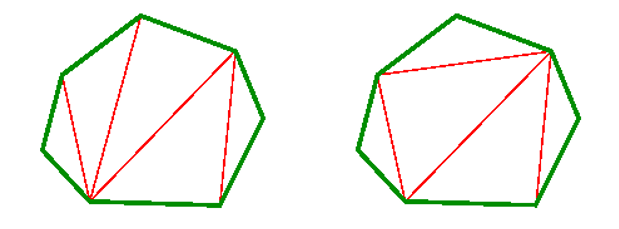
　　定义 d[i,j] 为从顶点 i 开始到顶点 j 所构成的多边形的最大三角剖分权和，则边 i→j 在此多边形内一定恰好属于一个三角形 i→j→k ，所以多边形就被分成了三部分：▲ikj 及其左右两部分子多边形。这个切割方法保证了两个子多边形它们的顶点编号是连续的。所以我们只需要每次将代表这个多边形的两个顶点（始、末）作为分割后的其中一个三角形的一条边，然后枚举第三个顶点 k 的情况，再依次分割下去直到分割完成。

　　所以，有状态转移方程：d[i,j] = max{d[i,k]+d[k,j]+w(i,j,k)}，时间复杂度为O(n³)

 

 

 

 

---

 

结合一道具体的题目来加深一下理解

题目链接：

　　https://cn.vjudge.net/problem/UVA-1331

题意：

　　给定一个n边形，要你求将这个n边形分割成若干三角形后，其中面积最大的三角形的最小值

分析：

　　典型的最优三角剖分问题，状态转移方程：d[i][j] = min{max{SΔijk,d[i][k],d[k][j]}} (i<k<j)

　　不过这里需要注意的是，这道题并没有指明这个多边形的凹凸性，所以对于凹多边形的情况，需要加上一个判断，即判断Δijk是否是合法的三角形，如果Δijk内部含有多边形的一个顶点，那么就是不合法的

　　具体分析细节，这篇博客写的不错https://blog.csdn.net/c20190102/article/details/75418824

代码：

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn = 60;
const int INF = 0x3f3f3f3f;
int x[maxn], y[maxn];
double dp[maxn][maxn];
int n;
double area(int a, int b, int c)
{
    double ans;
    ans = (x[a] * y[b] + x[b] * y[c] + x[c] * y[a] - x[a] * y[c] - x[b] * y[a] - x[c] * y[b]) * 1.0 / 2;
    return abs(ans);
}

int judge(int i, int j, int k)
{
    for(int v = 0; v < n; v++)
    {
        if(v == i || v == j || v == k)
            continue;
        else
        {
            double sum = area(i, j, v) + area(i, k, v) + area(j, k, v);
            if(abs(sum - area(i, j, k)) <= 0.001)    //因为有浮点数误差，这里初略认为小于0.001即为相等
                return 0;
        }
    }
    return 1;
}
int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        memset(dp, 0, sizeof(dp));
        cin >> n;
        for(int i = 0; i < n; i++)
        {
            cin >> x[i] >> y[i];
        }
        //i<k<j    注意边界
        for(int i = n - 3; i >= 0; i--)
        {
            for(int j = i + 2; j <= n - 1; j++)
            {
                dp[i][j] = INF;
                for(int k = i + 1; k < j; k++)
                {
                    if(judge(i, j, k))
                        dp[i][j] = min(dp[i][j], max(area(i, j, k), max(dp[i][k], dp[k][j])));
                }
            }
        }
        printf("%.1lf\n", dp[0][n - 1]);
    }
    return 0;
}