由数字三角形问题理解动态规划

先看几类数字三角形的问题，通过对这几个问题的分析来理解有关动态规划的基本思想

数字三角形I

问题描述：

　　有一个由正整数组成的三角形，第一行只有一个数，除了最下行之外 每个数的左下方和右下方各有一个数，从第一行的数开始，每次可以往左下或右下走一格，直到走到三角形底端，把沿途经过的数全部加起来作为得分。如何走，使得这个得分尽量大？

 

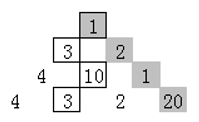
分析：

　　如何走，是一个决策问题，很容易联想到一种贪心策略是：每次选数字大的那个方向走。然而很明显，这种决策方案是错误的。因为如果按这种方案，得到的结果是1→3→10→3，总和为17，而正确的答案是：1→2→1→20，总和为24，这种方案错在了“目光短线“。

　　再次分析，赋予d[i,j]的含义为以(i,j)为首的三角形的最大和，那么这个问题就转换成了求d(1,1)。很明显，d[i,j]=a[i,j]+max(d[i+1,j],d[i+1,j+1])。这里体现的一个思想就是：将大问题分解为小问题，由小问题的求解来得到大问题的答案。

　　这个思路是正确的，那么接下来要考虑的一个问题就是如何计算了。有三种方法，递归、递推以及记忆化搜索，接下来就分析这三种计算方法的具体做法。

　　方法一：递归

int solve(int i, int j)
{
    if(i == n)
        return a[i][j];
    else
        return a[i][j] + max(solve(i + 1, j), solve(i + 1, j + 1));
}

　　这个方法存在不必要的重复计算，低效

　　方法二：递推

void solve()
{
    for(int j = 1; j <= n; j++)
        dp[n][j] = a[n][j];
    for(int i = n - 1; i >= 1; i--)
        for(int j = 1; j <= i; j++)
            dp[i][j] = a[i][j] + max(d[i + 1][j], dp[i + 1][j + 1]);
}

　　递推自底向上，避免了重复计算，时间复杂度为O(n²)

　　方法三：记忆化搜索

int solve(int i, int j)
{
    //首先初始化dp为-1 memset(dp,-1,sizeof(dp));
    if(i == n)
        return a[i][j];
    if(dp[i][j] >= 0)
        return dp[i][j];
    dp[i][j] = a[i][j] + max(solve(i + 1, j), solve(i + 1, j + 1));
    return dp[i][j];
}

　　这个方法就是在递归的基础上加上了记忆化，同样避免了重复计算，时间复杂度为O(n²)

对比这几种方法，可以看出重叠子问题(overlapping subproblems) 是动态规划展示威力的关键

通过这个例子，可以理解动态规划的基本思想：将大问题分解成小问题，建立子问题的描述，建立状态间的转移关系，使用递推或记忆化搜索来实现。而要使用好动态规划的几个关键的重点就是：状态的定义和状态转移方程。

数字三角形II

问题描述：

　　在数字三角形I的基础上稍微改变了一下。从第一行的数开始，除了某一次可以走到下一行的任意位置外，每次都只能左下或右下走一格，直到走到最下行，把沿途经过的数全部加起来。如何走，使得这个和尽量大？ 

分析：

　　这题的关键在于后效性问题，即先前的决策可能影响后续的决策，要消除后效性，就得拓展状态定义（加限制条件）来将有后效性的部分包含进去。

memset (maxx, 0, sizeof (maxx));
for(j = 1; j <= n; j ++)
{
    d[n][j][1] = d[n][j][0] = a[n][j];
    if(a[n][j] > max[n])
        maxx[n] = a[n][j];
}
for(i = n - 1; i >= 1; i--)
{
    for(j = 1; j <= i; j++)
    {
        d[i][j][0] = a[i][j] + max(d[i + 1][j][0], d[i + 1][j + 1][0]);
        if(d[i][j][0] > maxx[i])
            maxx[i] = d[i][j][0];
        d[i][j][1] = a[i][j] + max(d[i + 1][j][1], d[i + 1][j + 1][1], maxx[i + 1]);
    }
}

数字三角形III

问题描述：

　　在数字三角形I的基础上，问题变成了，如何走，使得这个和的个位数尽量大？ 

分析：

　　符合无后效性，但是却出现了另一个问题，那就是由子问题的最优解不能推出全局的最优解。比如看下面一个例子

 

　　对于灰色格子(2,1)来说，根据状态定义，d[2,1]=6（从 此格子出发路径上数之和的最大个位数），d[2,2]=0（无论怎么走，个位数都是0）， 根据前面的“递推方程”算出d[1,1]应是1，但实际上d[1,1]等于9。问题出在：全局最优解5-0-4-0并没有包含子问题最优解0-4-2，即不满足最优子结构。不满足最优子结构的情况通常也可以考虑扩展状态定义。

for(j = 1; j <= n; j++)
    d[n][j][a[n][j] % 10] = true;
for(i = n - 1; i >= 1; i--)
{
    for(j = 1; j <= i; j++)
    {
        for(k = 0; k <= 9; k++)
        {
            d[i][j][k] = false;
            t = (10 - a[i][j]) % 10;
            if(d[i + 1][j][t] || d[i + 1][j + 1][t])
                d[i][j][k] = true;
        }
    }
}

 总结：

动态规划可以解决的某类问题：

　　每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的。

其中，每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到，这个性质叫做最优子结构；而不管之前这个状态是如何得到的，这个性质叫做无后效性。