
线性代数
- 向量:定义了向量间的加法和标量乘法,且运算结果仍然属于向量
- 矩阵:表示一种线性映射,或者表示向量的集合
- 仿射:Ax+b (对一个向量进行线性映射之后加上另一个向量),1维的仿射是直线,二维的仿射是平面,n-1维的仿射是超平面
- 双线性映射:有两个参数,且对于每个参数,都是线性映射
- 矩阵的特征值和特征向量:可以理解为分别表示矩阵线性变换伸缩的方向和大小
- 矩阵行列式的值可以理解为在N维空间内,矩阵内列向量组成形状的”体积“(有符号数)
- 行列式的值是所有特征值的乘积
- 矩阵的迹是主对角线上元素的和,等于所有特征值的和
- 特征值分解只定义在方阵上,且需要有一组由特征向量组成的基;所有矩阵都存在SVD
- 特征值分解和SVD均由下面三个线性变换组成,对于SVD而言定义域和陪域可能有不同的维度
- 在定义域对基做变换
- 对基进行缩放,将定义域映射到陪域
- 在陪域对基做变换
向量微积分
- 链式法则
- 自动差分:通过中间变量构建函数的计算图,利用链式法则反向计算函数的梯度,自动差分是几乎所有深度学习框架的基础
概率与分布
- 对概率有两种理解:概率派(认为参数是固定的,所有参数源于数据本身)和贝叶斯派(参数服从分布,参数源于数据和先验)
- 样本空间:实验的所有可能结果集合
- 概率分布
- 概率质量函数(pmf):给定离散随机变量的取值,得到其对应的概率值
- 概率密度函数(pdf):随机变量在某一位置的概率密度
- 累积分布函数(cdf):随机变量小于某个值的概率
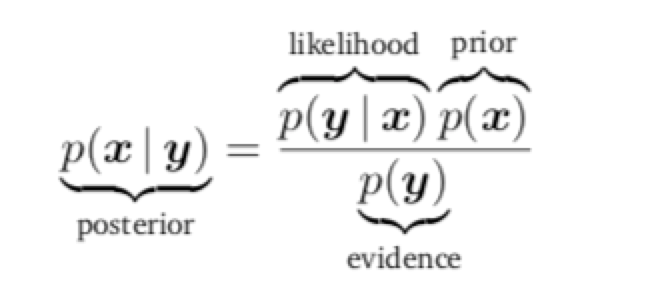
- 贝叶斯公式:
![]()
- 期望与方差
- 期望:关于X的函数与pdf的乘积的积分,当函数为x本身时此时的期望为均值,即E(x)
- 协方差:Cov(x, y) = E[(x - E(x))(y - E(y))] = E(xy) - E(x)E(y)
- 方差(与自身的协方差):V(x) = Cov(x, x)
- 标准差:方差的平方根
- 相关系数:
![]()
- 两个变量独立则p(x,y) = p(x)p(y), 两个变量独立则协方差为0,但协方差为0不一定独立,因为协方差为0只表示两个变量没有线性关系
连续最优化
- 训练一个机器学习模型常常归结为找到一组好的参数,这个过程就是通过最优化目标函数完成的
- 梯度下降:通常目标函数越小越好,参数空间最优解即目标函数取到最小值的时候,在实际应用中,很难通过找到梯度为0的解析解直接找到极小值,但由于梯度能够指引我们上升最快的方向(也是与等高线正交的方向),所以可以像负梯度的方向移动一步一步地找到极小值
- 凸函数,函数上任意两点之间的函数值都在两点间连线的下方,所有极小值都是最小值
- 带冲量的梯度下降:通过计算梯度的移动加权平均来记忆之前迭代的信息,能够减小震荡,加速收敛
- 随机梯度下降:通过计算一个样本的梯度来近似全局梯度,能够大大加快计算和迭代速度,节约内存/显存空间,但是会加剧震荡,也可能近似梯度的噪声有助于跳出局部极小值
- mini-batch梯度下降:计算一小批次样本的梯度来近似全局梯度,是GD和SGD的折中,能够享受到向量化批次计算的性能提升
- 三种GD计算得到的梯度都是真实梯度的无偏估计,所以都能够收敛(但方差不一致,所以单次迭代的效果不一致)
- 线性规划
- 二次规划
机器学习
- 机器学习的目标是找到一个模型以及相对应的参数使得predictor在未知的数据上能够表现好,通常有三个阶段
- 训练 / 参数估计
- 超参数调试 / 模型选择
- 预估 / 推理 (通常当模型是函数时,可称作预估,当模型是概率模型时,可称作推理)
- 经验风险:样本的平均loss;机器学习的通常策略就是经验风险最小化
- 当训练集的经验风险已经很小,但是测试集的预估风险比训练集的经验风险高得多时,说明模型对于未知样本不能很好地处理,也就是泛化能力不强,此时需要正则化,通过惩罚项来降低模型复杂程度,使模型不那么”精确“,增强泛化能力,使结构风险最小化
- 最大似然估计(MLE):最大化似然即最小化负对数似然,随着样本数增大,收敛于真实值,当样本数小时,方差大,所以容易过拟合
- 最大后验概率(MAP):利用参数的先验知识,最大化后验,因为证据(evidence)与参数无关,故等价于argmax(似然*先验),由于利用了先验信息,所以可以缓解过拟合的情况
线性回归
- 输出值是特征的线性组合,参数决定如何线性组合
- 假定noise和参数的先验服从高斯分布,可通过上述MLE和MAP推导,MAP推导的结果与正则项一致
EE问题
- 汤普森采样:贝塔分布的 a 参数看成是推荐后用户点击的次数,把分布的 b 参数看成是推荐后用户未点击的次数,则汤普森采样过程如下:
- 取出每一个候选对应的参数 a 和 b;
- 为每个候选用 a 和 b 作为参数,用贝塔分布产生一个随机数;
- 按照随机数排序,输出最大值对应的候选;
- 观察用户反馈,如果用户点击则将对应候选的 a 加 1,否则 b 加 1;
- 实际上在推荐系统中,可能要为每一个用户都保存一套参数,比如候选有 m 个,用户有 n 个,那么就要保存 2 m n个参数。
posted @
2020-09-23 20:28
排骨zzz
阅读(
188)
评论()
收藏
举报
![]()
![]()


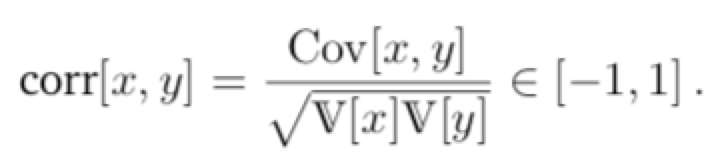

 浙公网安备 33010602011771号
浙公网安备 33010602011771号