P3376 【模板】网络最大流(luogu)
P3376 【模板】网络最大流(luogu)
最大流的dinic算法模板(采取了多种优化)
| 优化 | 时间 |
|---|---|
| inline+当前弧+炸点+多路增广 | 174ms |
| no 当前弧 | 175ms |
| no 炸点 | 249 |
自己对最大流算法的理解:
通过bfs对剩余图进行分层,剩余图中有流量的边(cap>0)才能bfs,然后dfs找增广路(满足dis[v]==dis[u]+1&&cap(u,v)>0)
各种优化(基本是在dfs(s,flow)上做的)的实现思路:
- 多路增广
通过记录从s流出的各个边增广的和,而不是找到目标t就返回(可以比较一下两段代码
//当前弧优化效果不明显可不加
struct Edge{
int v,nxt,cap;
}es[maxm];
void add(int u,int v,int cap){
//printf("db add %d->%d %d\n",u,v,cap);
es[cnt].v=v,es[cnt].cap=cap,es[cnt].nxt=head[u];
head[u]=cnt,cnt++;
}
int bfs(int s,int des){
CL(dep,-1);
queue<int> q;q.push(s);
dep[s]=1;
while(!q.empty()){
int tmp=q.front();q.pop();
for(int t=head[tmp];t!=-1;t=es[t].nxt){
int v=es[t].v,cap=es[t].cap;
if(cap>0&&dep[v]==-1){//dep[v]==-1代表未访问过
dep[v]=dep[tmp]+1;q.push(v);
if(v==des) return 1;
}
}
}
return dep[des]>-1?1:0;//是否能到达目的节点
}
int dfs(int s,int fl,int des){//fl流入s的流量,向s的出边增光
if(s==des||fl<=0) return fl;
int res=0; //多路增光
for(int t=head[s];fl&&t!=-1;t=es[t].nxt){
int v=es[t].v,cap=es[t].cap;
if(dep[v]==dep[s]+1){
int f=dfs(v,min(fl,cap),des);
es[t].cap-=f,es[t^1].cap+=f,res+=f;
fl-=f;
}
}
if(res==0) dep[s]=-2;//炸点优化
return res;
}
所以朴素的方式往往需要一次bfs,多次dfs;而经过多路扩展则是一次bfs,一次dfs(因为一次dfs就找全了所有增广路)
- 当前弧优化
思想是记录节点s应该流向的边,假设有这样s->1,s->2,s->3假设s->2时流量flow已经耗尽,那么下一次从3流出的应该从s->2开始(注意流向s可能有多条路径,flow只是流向s的某一条路径的流量)
for(int x=cur[s];x!=-1;x=e[x].next){
cur[s]=x;//当前弧优化
if(d[e[x].v]==d[s]+1&&e[x].cap>0){
//....
if(!flow) break;//当前已经没有流量
}
}
- 炸点优化
一个非目的点,流不出任何流量,那么以后都不用向该点流,所以d[s]=-2(以后dfs都不会流向它)
代码
//dinic 算法处理最大流问题
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
const int maxn=1e4+10;
const int maxm=1e5+10;
int s,t,n,m;
struct Edge{
int v,next,cap;
}e[maxm<<1];// begin from 0
int head[maxn];//-1 init
int cnt=-1;
int d[maxn];//init inf
int que[maxn<<2];
int cur[maxn];//for 当前弧优化
inline void add(int u,int v,int cap){//边从0开始
//e[cnt]=(Edge){v,head[u],cap};
cnt++;
e[cnt].v=v,e[cnt].next=head[u],e[cnt].cap=cap;
head[u]=cnt;
}
inline bool bfs(int ss,int tt){
memset(d,inf,sizeof(d));
memcpy(cur,head,sizeof(head));
int h=0,t=1;
que[0]=ss,d[ss]=1;
while(t>h){
int u=que[h];
h++;
for(int x=head[u];x!=-1;x=e[x].next){
int v=e[x].v;
if(d[v]>=inf&&e[x].cap>0){
d[v]=d[u]+1;//d[]用作vis[]
que[t++]=v;
}
}
}
//printf("db %d\n",d[tt]);
return d[tt]<inf;
}
inline int dfs(int s,int flow){
if(s==t||flow<=0) return flow;
int res=0;
for(int x=cur[s];x!=-1;x=e[x].next){
cur[s]=x;//当前弧优化
if(d[e[x].v]==d[s]+1&&e[x].cap>0){
int f=dfs(e[x].v,min(flow,e[x].cap));
e[x].cap-=f;
e[x^1].cap+=f;
res+=f;//通过res记录多路扩展
flow-=f;
if(!flow) break;//当前已经没有流量
}
}
if(!res) d[s]=-2;//炸点优化,s没能流出任何流量,那么本次bfs下的dfs无需再向s流
return res;
}
inline void dbgraph(){
for(int i=1;i<=n;i++){
printf("%d:",i);
for(int x=head[i];x!=-1;x=e[x].next){
if(e[x].cap>0) printf("%d\t",e[x].v);
}
printf("\n");
}
}
int main(){
//freopen("in.txt","r",stdin);
scanf("%d %d %d %d",&n,&m,&s,&t);
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++){
int u,v,cap;
scanf("%d %d %d",&u,&v,&cap);
add(u,v,cap);
add(v,u,0);
}
//dbgraph();
int ans=0;
while(bfs(s,t)){
//printf("in bfs\n");
ans+=dfs(s,inf);
}
printf("%d\n",ans);
//fclose(stdin);
return 0;
}
补充一点
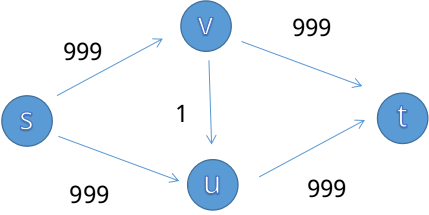
从EK算法到Dinic算法有很重要的原因在于下面一张图