LeetCode28. 实现 strStr()

题目

分析

经典的一道字符串匹配题目，有两种方法，朴素的暴力和KMP算法

这里不仅要能熟练写出朴素算法也要会写KMP算法

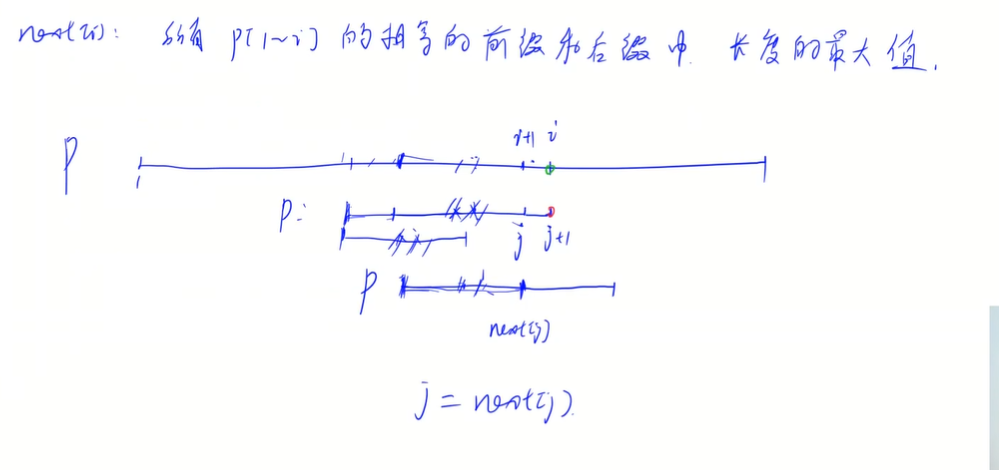
KMP算法推荐 y 总的模板，如下：

我们一般字符串从1开始，所以一开始加个空字符

// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度
求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )  //从2开始，1本身就是平凡的，前后缀相同，ne[1] = 0不用求了
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // 匹配成功后的逻辑
    }
}

 

 

 

代码

朴素算法

时间复杂度O(m * n)

class Solution {
public:
    int strStr(string h, string n) {
        if(n.empty() || h.empty()) return 0;

        int i = 0,j = 0;
        
        while(i < h.size() && j < n.size()){
           if(h[i] == n[j]) i++,j++;
           else{
               i = i - j + 1; // 回退
               j = 0;
           }
        }

        if(j == n.size()){
            return i - j;
        }else {
            return -1;
        }
    }
};

KMP算法

时间复杂度O（n + m ）

class Solution {
public:
    int strStr(string s, string p) {
        if(!p.size()) return 0;
        int n = s.size(), m = p.size();
        s = ' ' + s;
        p = ' ' + p;

        vector<int>next(m+1);

        //首先先求next数组，其实相当于两个p串匹配
        for(int i = 2,j = 0;i <= m;i++){ //从2开始next[1]为0,i 要小于等于m
            while(j && p[i] != p[j+1]) j = next[j];
            if(p[i] == p[j+1]) j++;
            next[i] = j;
        }

        //然后求s,p匹配
        for(int i = 1,j = 0;i <= n;i++){
            while(j && s[i] != p[j+1]) j = next[j];
            if(s[i] == p[j+1]) j++;
            if(j == m) return i - m;
        }

        return -1;
    }
};