最长上升子序列

题目

分析

下图为y总的递推公式分析

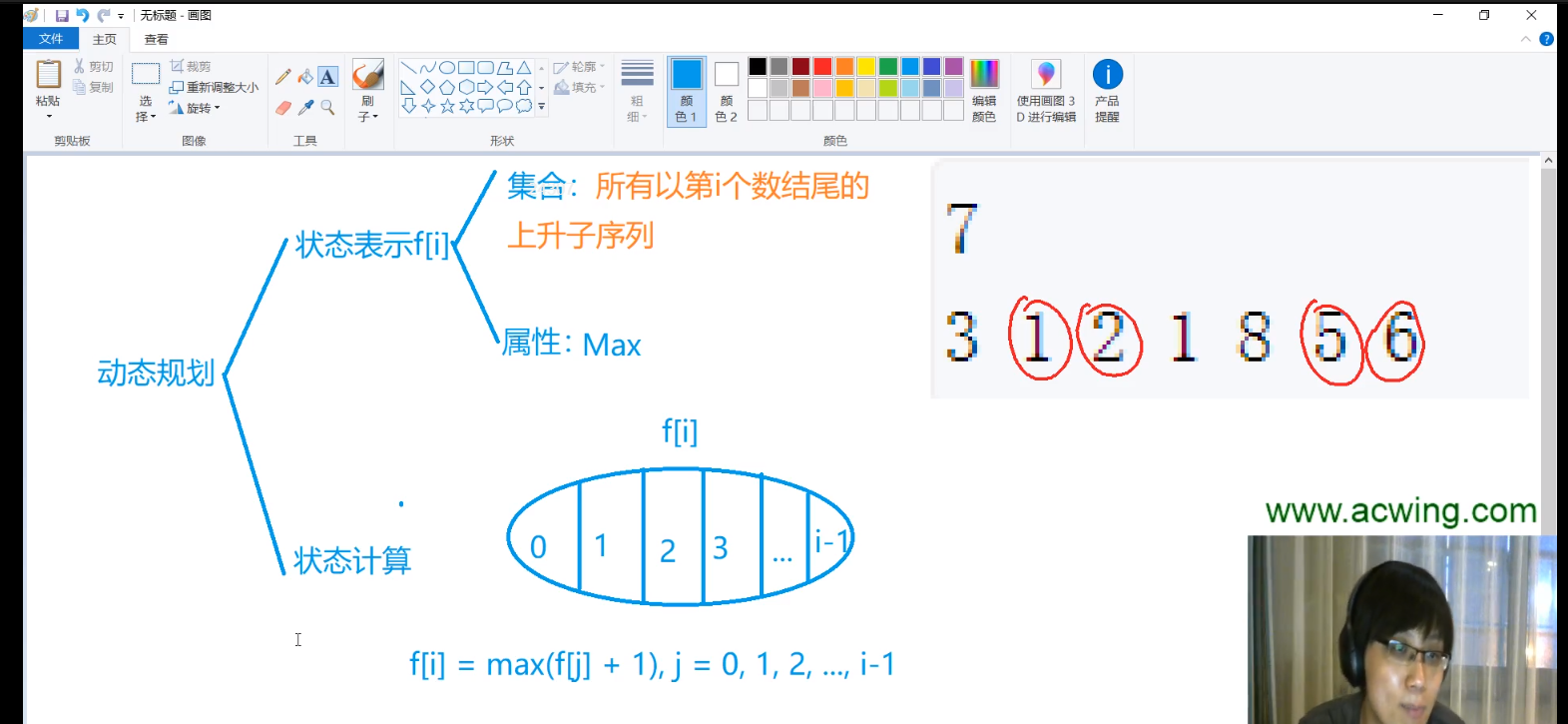
dp[i] 表示 开头到 i 处最长上升子序列的长度。思考递推公式，如何由小的状态推大状态？

以第 i 个数结尾的上升子序列的构成：仅含 i 位置这一个数（意味着前面上升子序列）或者 若a[i - 1] < a[i] 时，dp[i - 1] + 1。由于dp[i]存放的是最长上升子序列，所以要找到从0 到 i - 1的最长子序列长度 再加上 i 处本身的元素。所以递推公式：

dp[i] = max(dp[j]+1),j = 0,1,2....i-1，且有a[j] < a[i] 

代码

#include<iostream>
#include<algorithm>
using namespace std;

int main(){
    int n;
    scanf("%d",&n);
    vector<int>a(n);//存放序列
    vector<int>dp(n,0);
    for(int i = 0;i < n;i++){
        scanf("%d",&a[i]);
    }
    for(int i = 0;i < n;i++){
        dp[i] = 1;//最长子序列只含有一个数
        for(int j = 0;j < i;j++){ //从头遍历到i-1找到最大单增子序列最大值
            if(a[j] < a[i]){
                dp[i] = max(dp[i],dp[j] + 1);
            }
        }
    }
    int res = 0;
    for(int i = 0; i < n;i++){
        if(res < dp[i]) res = dp[i];
    }
    cout<<res;
    return 0;
}

时间复杂度  = 状态数 *　转移数量，状态数是n，转移数量因为每次要遍历下末位置之前的所以也为n

所以时间复杂度为O(n²)

如何存储打印最长子序列？重点掌握

就是开个数组保存一下是如何转移的

#include<iostream>
#include<algorithm>
#include<stack>
using namespace std;

int main(){
    int n;
    scanf("%d",&n);
    vector<int>a(n);//存放序列
    vector<int>g(n,0); //存放转移位置
    vector<int>dp(n,0);
    
    for(int i = 0;i < n;i++){
        scanf("%d",&a[i]);
    }
    for(int i = 0;i < n;i++){
        dp[i] = 1;//最长子序列只含有一个数
        g[0] = 0;//开始只有头元素
        for(int j = 0;j < i;j++){ //从头遍历到i-1找到最大单增子序列最大值
            if(a[j] < a[i]){
                //dp[i] = max(dp[i],dp[j] + 1);
                if(dp[i] < dp[j]+1){
                    dp[i] = dp[j] + 1;
                    g[i] = j;//记录是从哪一个转移过来的，就是最长子序列的上一个元素
                }
                    
            }
        }
    }
 
    //找到最长子序列的尾部下标
    int res = 0;
    for(int i = 0;i < n;i++){
        if(dp[res] < dp[i])
            res = i;
    }
    int len = dp[res];
    int k = res;
    stack<int>s;
    for(int i = 1;i <= len;i++){
        s.push(a[k]);
        k = g[k];
    }
    while(!s.empty()){
        cout<<s.top()<<" ";
        s.pop();
    }
    
    return 0;
}