PKU 3020 Antenna Placement(拆点+最小边覆盖)(最大匹配)
一个矩形中，有N个城市’*’，现在这n个城市都要覆盖无线，若放置一个基站，那么它至多可以覆盖相邻的两个城市。
问至少放置多少个基站才能使得所有的城市都覆盖无线？
提示：看清楚题目，'*'是城市，'o'是空地，椭圆的天线覆盖范围要覆盖的是城市'*',而不是覆盖空地
解题思路：关键是建模构图
每两个相邻的星号连一条边，很明显这是一道求二分图的最小边覆盖问题（注意不是最小点覆盖）
那么接下来需要确认的是，究竟是求 有向二分图的最小边覆盖，还是求 无向二分图的最小路覆盖
因为有向和无向是截然不同的计算方法。
要确认是构造有向图，还是构造无向图，那么就需要先根据题意，看看构造二分图时所使用的方式，更适合构造哪一种二分图。
然后就进入了本题难点：如何构造二分图
首先要明确的是，输入的一堆“圈圈星星”可以看做是一张大地图，地图上有所有城市的坐标，但是这里有一个误区：不能简单地把城市的两个x、y坐标作为准备构造的二分图的两个顶点集。
城市才是要构造的二分图的顶点！
构造方法如下：
例如输入：
*oo
***
o*o
时，可以抽象为一个数字地图：
100
234
050
数字就是根据输入的城市次序作为该城市的编号，0代表该位置没有城市。
然后根据题目的“范围”规则，从第一个城市开始，以自身作为中心城市，向四个方向的城市进行连线（覆盖）
因此就能够得到边集：
e12 e21 e32 e43 e53
e23 e34
e35
可以看到，这些边都是有向边，但是每一条边都有与其对应的一条相反边。
即任意两个城市（顶点）之间的边是成对出现的
那么我们就可以确定下来，应该 构造无向二分图（其实无向=双向）
因为若要构造有向的二分图时，需要判断已出现的边，是很麻烦的工作
为了把有向图G构造为无向二分图，这里需要引入一个新名词“拆点”
其实就是把原有向图G的每一个顶点都”拆分（我认为复制更准确）”为2个点，分别属于所要构造的二分图的两个顶点集
例如在刚才的例子中抽出一条有向边e12举例说明：
复制顶点1和顶点2，使得1，2∈V1； 1’，2’∈V2 ，不难发现|V1|=|V2|
根据边e12和e21，得到无向二分图：
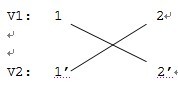
那么同理就可以得到刚才的例子的 无向二分图为：
再继而通过无向二分图，以V1的元素作为row，V2的元素作为col，构造 可达矩阵 存储到计算机
1’ 2’ 3’ 4’ 5’
1 F T F F F
2 T F T F F
3 F T F T T
4 F F T F F
5 F F T F F
接下来就是要求这个 无向二分图的最小边覆盖 了
利用公式：
无向二分图的最小边覆盖 = 顶点数 – 最大二分匹配数/2
顶点数：就是用于构造无向二分图的城市数，即进行“拆点”操作前的顶点数量
最大二分匹配数之所以要除以2，是因为进行了“拆点”，在构图过程中，匹配是双向的，即<u,v> 和<v,u>都算匹配，因此匹配数多了1倍，因此除以2得到原图的真正的匹配数。
最后剩下的问题就是求最大二分匹配数了，用匈牙利算法，这就不多说了，参考PKU3041的做法，基本一摸一样
从这道题得出了一个结论：
当二分图的两个顶点子集基数相等时，该二分图所有顶点的匹配数 等于 任意一个顶点子集匹配数的2倍
#include<iostream> #include<cstring> #include<algorithm> #define maxn 410 using namespace std; bool vis[maxn]; char c[maxn][maxn]; int tx,ty,g[maxn][maxn]; int link[maxn],map[maxn][maxn]; int dir[4][2]={0,1,0,-1,-1,0,1,0};//上下左右 bool Find(int x){ for(int i=1;i<=ty;i++){//匹配右侧顶点集 if(g[x][i]&&!vis[i]){ vis[i]=true; if(!link[i]||Find(link[i])){ link[i]=x; return true; } } } return false; } int maxMatch() { int ans=0; memset(link,0,sizeof(link)); for(int i=1;i<=tx;i++){//枚举左侧顶点集 memset(vis,false,sizeof(vis)); if(Find(i)) ans++; } return ans; } int main(){ int T,m,n; cin>>T; while(T--){ memset(g,0,sizeof(g)); memset(c,0,sizeof(c)); memset(map,0,sizeof(map)); cin>>m>>n; int cnt=0; for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ cin>>c[i][j]; if(c[i][j]=='*') map[i][j]=++cnt; } } tx=cnt,ty=cnt; for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ if(map[i][j]){ for(int k=0;k<4;k++){ int nx=i+dir[k][0]; int ny=j+dir[k][1]; if(nx<1||nx>m||ny<1||ny>n) continue; if(map[nx][ny]) g[map[i][j]][map[nx][ny]]=1; } } } } printf("%d\n",cnt-maxMatch()/2); } }
PS:之前一直想不通一点，为什么PKU3041可以直接用x,y坐标作边集。
PKU3041最后的图是对整行或者整列操作，拥有相同x坐标或y坐标的点看成了相同的，但这里是对单独的点操作，考虑它周围的点是否能连成边，再看能不能覆盖掉，这是不同的地方。
