基于向量判断线段之间的位置关系

我们知道在平面上两条直线的关系只有两种，也就是平行或相交，其中共线是平行的一种特殊情况。

那么对于线段，由于不能无限延长，所以会在直线的关系上有所扩展，可以按照平行线和相交线的大类再作一次分类：

1. 两线段所在的直线相交
   1. 两线段相交 （包括一个线段的顶点在另外一个线段的情况）
   2. 两线段不相交，即没有交点
2. 两线段所在的直线平行（包括共线）
   1. 两线段平行但不共线
   2. 两线段共线但不重合
   3. 两线段共线且有重合

所以两个线段间细分也就只有上面 5 种位置关系，那么有什么办法来判断两个线段的位置关系呢？一般的做法可以根据两点求解直线方程，然后按照解析几何的方式来判断直线的位置关系，但是这种方式需要考虑的情况比较多并且实现非常繁琐，例如如果考虑到斜率那么还需要单独考虑直线和 x 轴垂直的情况，所以我们不妨变换一下思路，将两个线段看作是两个向量，看这样能否对问题起到简化的作用。
首先我们会想到向量的叉乘，因为向量叉乘是否为零向量直接说明两个向量是否平行（也叫共线向量，平行和共线是等价的，所以下面我们不再单独说明），如果两个向量叉乘结果为零向量说明两个向量平行或共线，否则则说明不共线，因此单纯根据这个关系就可以实现大的归类，然后可以再进一步细分。

因此我们假设有线段：AB 和 CD，坐标分别为：\(A(x_a, y_a),B(x_b,y_b),C(x_c,y_c),D(x_d,y_d)\), 所以有：\(\vec{AB}=(x_b-x_a, y_b-y_a), \vec{CD}=(x_d-x_c, y_d-y_c)\), 然后即可计算两个向量的叉乘，两个向量叉乘的坐标表示如下：

\[\begin{align} &设: \vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2) \\ &有: \vec{a}\times\vec{b}=\begin{vmatrix} x_1 & y_1 \\ x_2 & y_2 \end{vmatrix} \vec{k}=(x_1y_2-x_2y_1)\vec{k} \end{align} \]

其中 \(\vec{k}\) 是和两个向量所在平面垂直的向量，在右手坐标系中方向满足右手定则，而在左手坐标系中方向满足左手定则，所以无论是哪个坐标系结果都是一样的，因为 \(\vec{k}\) 的方向确定，所以系数的正负就决定的结果的方向，假设在右手坐标系中，向量 \(\vec{a}\) 转到 \(\vec{b}\) 是逆时针方向，则结果为正即和 z 轴正方向一致，反之则结果为负，方向和 z 轴的正方向相反。
根据上面的基本原理，我们可以得到：如果 \(\vec{AB} \times \vec{CD} = \vec{0}\) 则 \(\vec{AB}\) 和 \(\vec{CD}\) 两个向量平行，反之则不平行，然后我们根据这两种情况分别作讨论。

1.两个向量不平行

在不平行的前提下我们就要判断是否相交了，我们先看相交的情况，如下图所示：

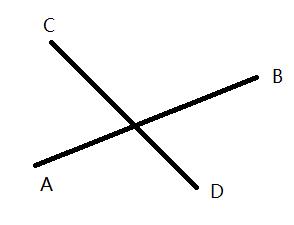
这个时候我们如果以点 A 为参考点，同时连接 AC 和 AD，连同已有的 AB，构成一组向量：\(\vec{AC},\vec{AD},\vec{AB}\)

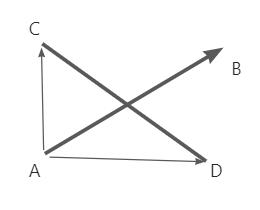
可以发现 \(\vec{AB}\) 到 \(\vec{AC}\) 是逆时针旋转，而 \(\vec{AB}\) 到 \(\vec{AD}\) 是顺时针旋转，所以有：

\[(\vec{AB}\times\vec{AC})\cdot(\vec{AB}\times\vec{AD}) < 0 \tag{0} \]

也就是说两个叉积是异号的，这说明了点 C 和点 D 是分布在线段 AB 两侧的，但这也说明不了两个线段相交，因为有可能 AB 没有跨过 CD, 所以这个时候很明显需要再以 CD 任何一个点为起点，比如点 C, 构造向量组：\(\vec{CD},\vec{CA},\vec{CB}\) 如下图：

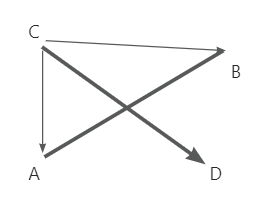
所以还需要满足：

\[(\vec{CD}\times\vec{CA})\cdot(\vec{CD}\times\vec{CB})<0 \tag{1} \]

所以只有同时满足上面两个条件，就可以得到两个线段是相交的，还是还不能说是充要条件，因为我们还要考虑线段的端点正好落在另外一个线段上的情况，例如：

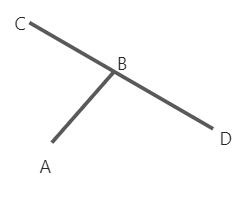
这种情况只满足上面的公式 0, 而不满足公式 1, 甚至有更极端的情况：

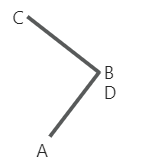
这种情况上面两式都不满足，但是我们不妨单独拉出来看，分别看公式 0 和 1 的两部分。
对于公式 0 有：

\[\vec{AB}\times\vec{AC} \ne \vec{0}, \vec{AB}\times\vec{AD}=\vec{0} \]

也就是其中有一个结果为零向量，对于公式 1 同样有：

\[\vec{CD}\times\vec{CA}\ne\vec{0},\vec{CD}\times\vec{CB}=\vec{0} \]

同样是一个结果为零向量，另外一个结果为非零向量。

综上我们可以得到线段 AB 和 CD 相交的充要条件是：

\[\begin{align} &(\vec{AB}\times\vec{AC})\cdot(\vec{AB}\times\vec{AD}) < 0 \\ &或 \\ &在 \ \vec{AB}\times\vec{AC} \ 与 \ \vec{AB}\times\vec{AD} \ 中,有且只有一个为零向量 \end{align} \]

并且：

\[\begin{align} &(\vec{CD}\times\vec{CA})\cdot(\vec{CD}\times\vec{CB})<0 \\ &或 \\ &在 \ \vec{CD}\times\vec{CA} \ 与 \ \vec{CD}\times\vec{CB} \ 中, 有且只有一个为零向量 \end{align} \]

所以线段 AB 和 CD 相交的充要条件是同时满足上面两个条件。

2.两个向量共线

这种情况下就要分析最开始说的那 3 种情况了

2.1.两个线段不在同一条直线上

如下图所示：

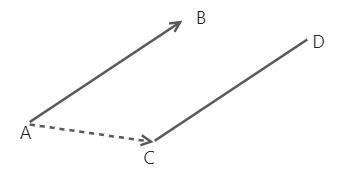
这种情况我们以其中任意一个线段作为向量，然后选取该线段其中一个端点连接另一条线段的任意一个端点，则有：

\[\vec{AB}\times\vec{AC} \ne \vec{0} \]

也就是说只要结果不是零向量，就说明两条线段不在同一条直线上，否则就必然在同一条直线上。

2.2.两个线段在同一条直线上但不重合

如下图所示：

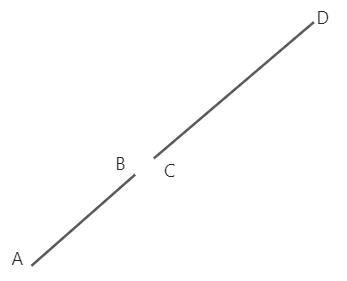
像这种情况就是两条线段虽然在同一条直线上但是并没有重合部分，这种情况下需要先将 A B C D 这 4 个点的坐标进行排序，排序规则为：先按照横坐标排序，横坐标相同的情况下按照纵坐标排序，排完序之后的结果中，如果满足下面的条件则必然不重合：

1. 前两个点和后两个点分别是两个线段的端点。（非交错出现）
2. 第 2 个点和第 3 个点的坐标不能完全相同。
   条件 2 主要为了排除两个端点正好重合的情况，这种情况排序有可能出现交错的情况。
   另外还有一种判断交集的方法，可以将两个线段分别投影到 x 轴 和 y 轴上，可以分为下面的几种情况：
3. 与 y 轴平行，所有点的横坐标都相等，且纵坐标区间没有交集。
4. 与 x 轴平行，所有点的纵坐标都相等，且横坐标区间没有交集。
5. 所有点的纵坐标和横坐标都没有交集。
   只要满足上面情况中的 1 种，就说明线段之间不重合，也就是说上面的条件是或的关系。
   还有一种非常简单的的判断是两个线段中，其中一个线段较大的点小于另外一个线段的较小点或者其中一个线段较小点大于另外一个线段的较大点，也可以说明之间没有重合，点的大小比较同样满足上面的排序规则，这也是一种非常通俗的判断方式。

2.3.两个线段在同一条直线上并且有重合

如果不满足上面的条件则表示有重合。

综上，我们就对平面中两个线段的关系进行了详细的判别分析，利用向量叉乘计算的好处是我们不需要解方程，而是直接进行正向运算加上部分的判断即可得出结果，如果编写程序那么计算速度非常快，并且精度也比较高。

本文的分享就是这些了，感谢您的耐心阅读，如有错误欢迎指正！