挑战算法题:四数之和
昨天解决了三数之和,感兴趣或者不知道怎么解的同学可以先看双指针妙解三数之和,今天继续试试解开:四数之和。
变量变多了一个,但是难度还是medium,因为思路是类似的。
具体题目如下所示:
Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
0 <= a, b, c, d < n
a, b, c, and d are distinct.
nums[a] + nums[b] + nums[c] + nums[d] == target
You may return the answer in any order.
Example 1:
Input: nums = [1,0,-1,0,-2,2], target = 0
Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
Example 2:
Input: nums = [2,2,2,2,2], target = 8
Output: [[2,2,2,2]]
Constraints:
1 <= nums.length <= 200
-109 <= nums[i] <= 109
-109 <= target <= 109
学习的过程就是搭积木的过程,解决问题的过程也是一样的,先想想可不可以把四数之和转化为三数问题。三数问题我们是把其中一个数字作为固定元素,通过循环去主义匹配剩下2个数字。而剩下两个数字就可以用两个指针不断移动,确定解法。同样的,四数问题,可以转换成2个循环去确定2个固定元素,剩下2个元素依然用双指针去移动确立。
代码实现如下所示:
/**
* @param {number[]} nums
* @param {number} target
* @return {number[][]}
*/
var fourSum = function(nums, target) {
// Sort the array
nums.sort((a, b) => a - b);
const result = [];
for (let i = 0; i < nums.length - 3; i++) {
// Skip the duplicated items
if (i > 0 && nums[i] === nums[i - 1]) continue;
for (let j = i + 1; j < nums.length - 2; j++) {
// Skip the duplicated items
if (j > i + 1 && nums[j] === nums[j - 1]) continue;
let left = j + 1;
let right = nums.length - 1;
while(left < right) {
const sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum === target) {
result.push([nums[i], nums[j], nums[left], nums[right]]);
while(left < right && nums[left] === nums[left+1]) {
left += 1;
}
while(left < right && nums[right] === nums[right-1]) {
right -= 1;
}
left += 1;
right -= 1;
} else if (sum > target) {
right -= 1;
} else {
left += 1;
}
}
}
}
return result;
}
执行之后的效率中规中矩,如图所示:

到这里本该结束了,但是这个算法其实还有提升空间。在left和right指针跳过重复的值的过程,我们可以提前退出循环,如下所示:
while(left < right) {
const sum = nums[i] + nums[j] + nums[left] + nums[right];
const remaining = target - sum;
if (remaining > nums[right] - nums[left]) break; // Jump out the loop, because there is no item can match it
}
重新提交之后,执行时间减少明显,内存使用保持不变:
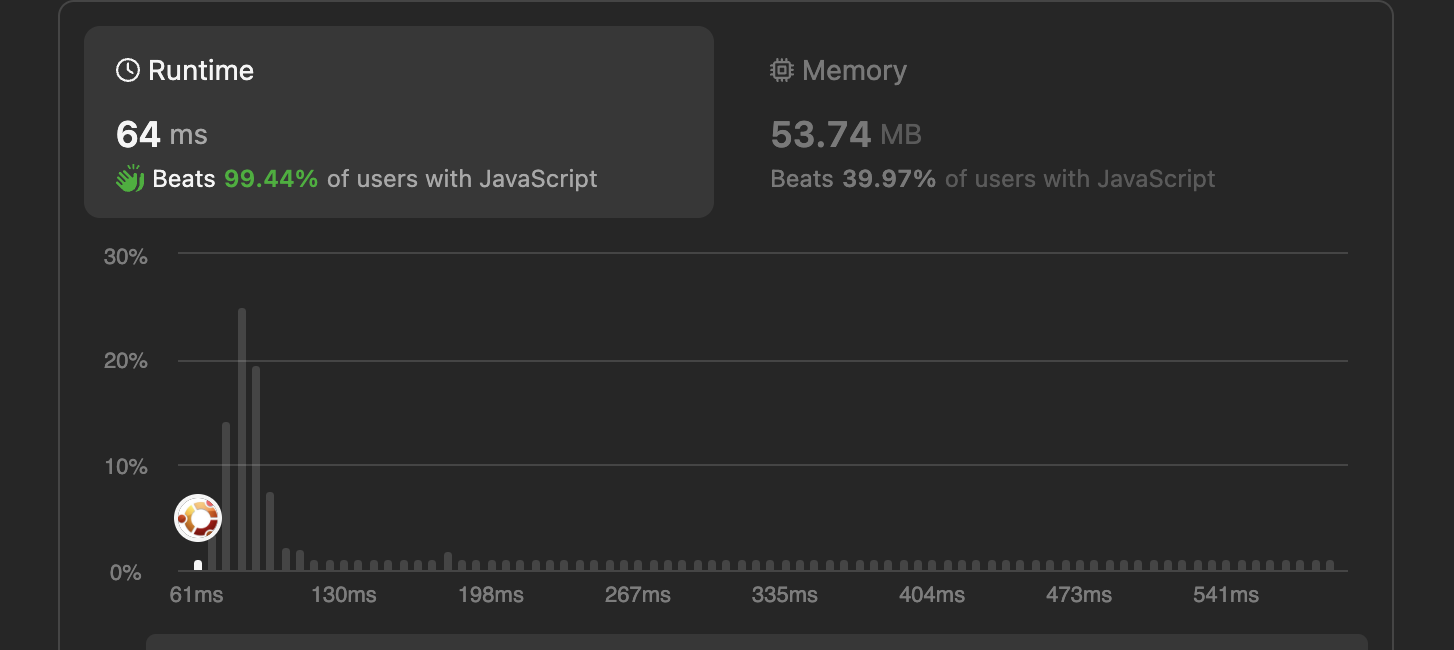
总结
这一类求多个元素之和等于给定值的算法题,都可以用双指针去解决,注意感受指针移动的过程以及培养转化已知问题的能力。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通