如何用Python实现常见机器学习算法-3
三、BP神经网络
1、神经网络模型
首先介绍三层神经网络,如下图
输入层(input layer)有三个units(![]() 为补上的bias,通常设为1)
为补上的bias,通常设为1)
![]() 表示第j层的第i个激励,也称为单元unit
表示第j层的第i个激励,也称为单元unit
![]() 为第j层到第j+1层映射的权重矩阵,就是每条边的权重
为第j层到第j+1层映射的权重矩阵,就是每条边的权重
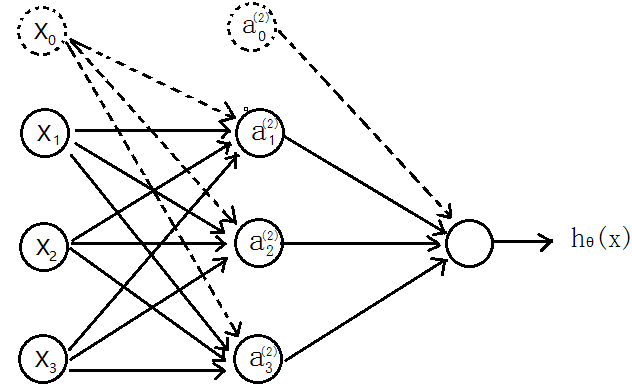
所以可以得到:
隐含层:
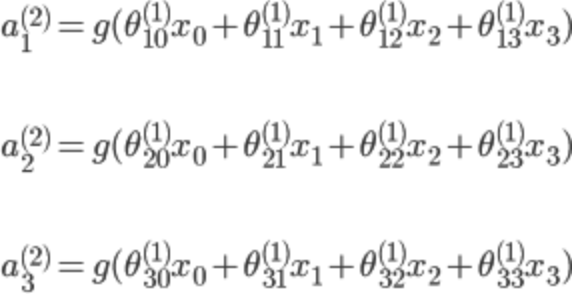
输出层:
![]()
其中,S型函数![]() ,也成为激励函数
,也成为激励函数
可以看出![]() 为3✖️4的矩阵,
为3✖️4的矩阵,![]() 为1✖️4的矩阵
为1✖️4的矩阵
![]() ==》j+1的单元数x(j层的单元数+1)
==》j+1的单元数x(j层的单元数+1)
2、代价函数
假设最后输出的![]() ,即代表输出层有K个单元
,即代表输出层有K个单元
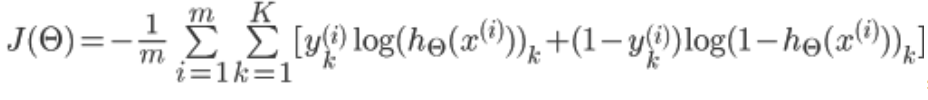
其中,![]() 代表第i个单元输出与逻辑回归的代价函数
代表第i个单元输出与逻辑回归的代价函数
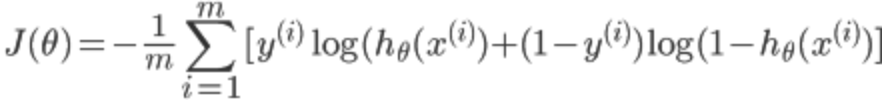
差不多,就是累加上每个输出(共有K个输出)
3、正则化
L-->所有层的个数
![]() -->第l层unit的个数
-->第l层unit的个数
正则化后的代价函数为
![]()
![]() 共有L-1层,然后是累加对应每一层的theta矩阵,注意不包含加上偏置项对应的theta(0)
共有L-1层,然后是累加对应每一层的theta矩阵,注意不包含加上偏置项对应的theta(0)
正则化后的代价函数实现代码:
1 # 代价函数 2 def nnCostFunction(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda): 3 length = nn_params.shape[0] # theta的中长度 4 # 还原theta1和theta2 5 Theta1 = nn_params[0:hidden_layer_size*(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1) 6 Theta2 = nn_params[hidden_layer_size*(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1) 7 8 # np.savetxt("Theta1.csv",Theta1,delimiter=',') 9 10 m = X.shape[0] 11 class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系 12 # 映射y 13 for i in range(num_labels): 14 class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值 15 16 '''去掉theta1和theta2的第一列,因为正则化时从1开始''' 17 Theta1_colCount = Theta1.shape[1] 18 Theta1_x = Theta1[:,1:Theta1_colCount] 19 Theta2_colCount = Theta2.shape[1] 20 Theta2_x = Theta2[:,1:Theta2_colCount] 21 # 正则化向theta^2 22 term = np.dot(np.transpose(np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1)))),np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1)))) 23 24 '''正向传播,每次需要补上一列1的偏置bias''' 25 a1 = np.hstack((np.ones((m,1)),X)) 26 z2 = np.dot(a1,np.transpose(Theta1)) 27 a2 = sigmoid(z2) 28 a2 = np.hstack((np.ones((m,1)),a2)) 29 z3 = np.dot(a2,np.transpose(Theta2)) 30 h = sigmoid(z3) 31 '''代价''' 32 J = -(np.dot(np.transpose(class_y.reshape(-1,1)),np.log(h.reshape(-1,1)))+np.dot(np.transpose(1-class_y.reshape(-1,1)),np.log(1-h.reshape(-1,1)))-Lambda*term/2)/m 33 34 return np.ravel(J)
4、反向传播BP
上面正向传播可以计算得到J(θ),使用梯度下降算法还需要求它的梯度
BP反向传播的目的就是求代价函数的梯度
假设4层的神经网络,![]() 记为-->l层第j个单元的误差
记为-->l层第j个单元的误差
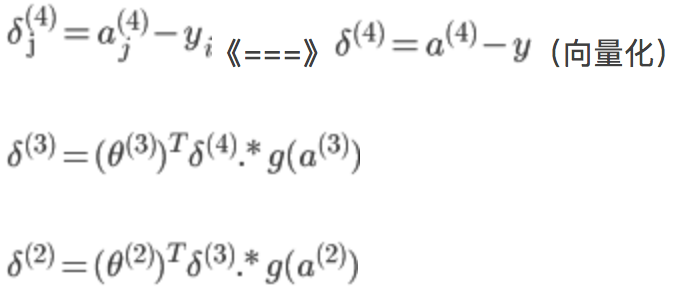
没有![]() ,因为对于输入没有误差,因为S型函数
,因为对于输入没有误差,因为S型函数![]() 的倒数为:
的倒数为:
![]()
所以上面的![]() 和
和![]() 可以在前向传播中计算出来
可以在前向传播中计算出来
反向传播计算梯度的过程为:
![]()
for i=1-m:
![]()
正向传播计算![]() (l=2,3,4...L)
(l=2,3,4...L)
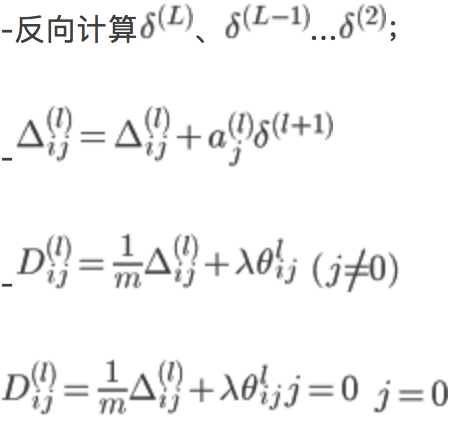
最后![]() ,即得到代价函数的梯度
,即得到代价函数的梯度
代码实现:
1 # 梯度 2 def nnGradient(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda): 3 length = nn_params.shape[0] 4 Theta1 = nn_params[0:hidden_layer_size*(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1) 5 Theta2 = nn_params[hidden_layer_size*(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1) 6 m = X.shape[0] 7 class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系 8 # 映射y 9 for i in range(num_labels): 10 class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值 11 12 '''去掉theta1和theta2的第一列,因为正则化时从1开始''' 13 Theta1_colCount = Theta1.shape[1] 14 Theta1_x = Theta1[:,1:Theta1_colCount] 15 Theta2_colCount = Theta2.shape[1] 16 Theta2_x = Theta2[:,1:Theta2_colCount] 17 18 Theta1_grad = np.zeros((Theta1.shape)) #第一层到第二层的权重 19 Theta2_grad = np.zeros((Theta2.shape)) #第二层到第三层的权重 20 21 Theta1[:,0] = 0; 22 Theta2[:,0] = 0; 23 '''正向传播,每次需要补上一列1的偏置bias''' 24 a1 = np.hstack((np.ones((m,1)),X)) 25 z2 = np.dot(a1,np.transpose(Theta1)) 26 a2 = sigmoid(z2) 27 a2 = np.hstack((np.ones((m,1)),a2)) 28 z3 = np.dot(a2,np.transpose(Theta2)) 29 h = sigmoid(z3) 30 31 '''反向传播,delta为误差,''' 32 delta3 = np.zeros((m,num_labels)) 33 delta2 = np.zeros((m,hidden_layer_size)) 34 for i in range(m): 35 delta3[i,:] = h[i,:]-class_y[i,:] 36 Theta2_grad = Theta2_grad+np.dot(np.transpose(delta3[i,:].reshape(1,-1)),a2[i,:].reshape(1,-1)) 37 delta2[i,:] = np.dot(delta3[i,:].reshape(1,-1),Theta2_x)*sigmoidGradient(z2[i,:]) 38 Theta1_grad = Theta1_grad+np.dot(np.transpose(delta2[i,:].reshape(1,-1)),a1[i,:].reshape(1,-1)) 39 40 '''梯度''' 41 grad = (np.vstack((Theta1_grad.reshape(-1,1),Theta2_grad.reshape(-1,1)))+Lambda*np.vstack((Theta1.reshape(-1,1),Theta2.reshape(-1,1))))/m 42 return np.ravel(grad)
5、BP可以求梯度的原因
实际是利用了链式求导法则
因为下一层的单元利用上一层的单元作为输入进行计算
大体的推导过程如下,最终我们是想预测函数与已知的y非常接近,求均方差的梯度沿着此梯度方向可使代价函数最小化。可对照上面求梯度的过程。
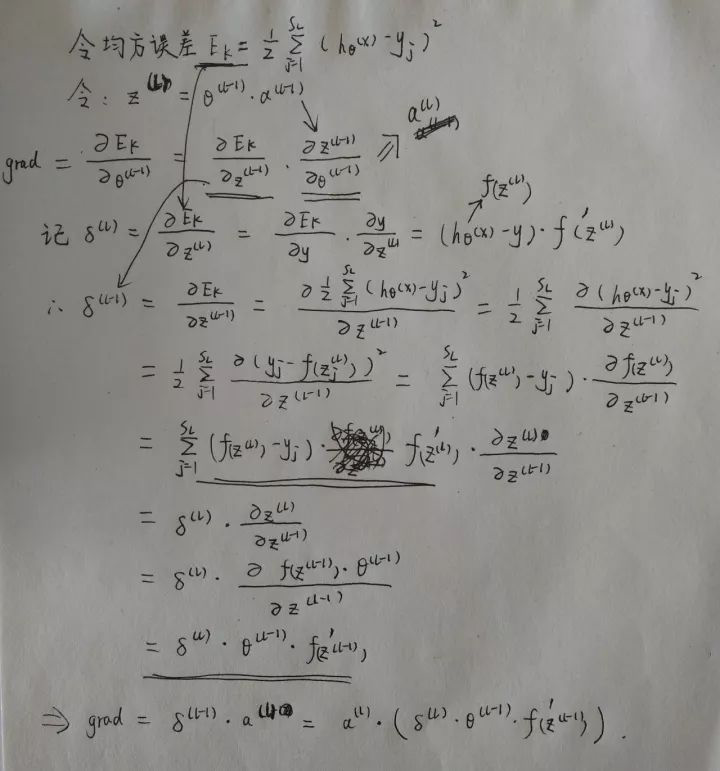
求误差更详细的推导过程:
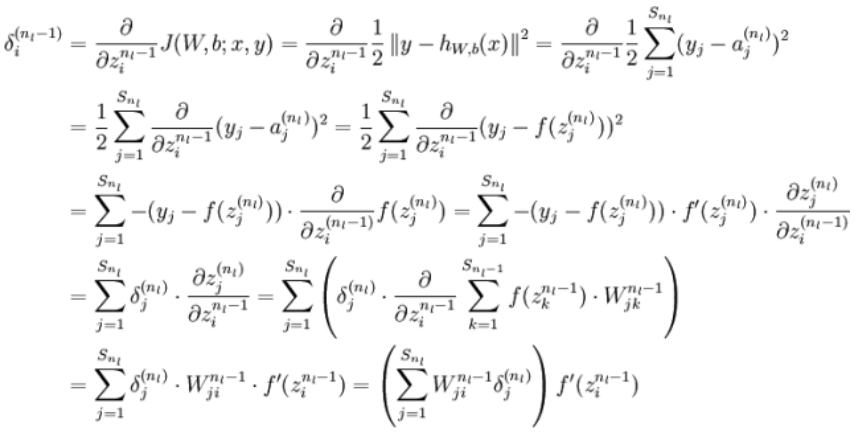
6、梯度检查
检查利用BP求的梯度是否正确
利用导数的定义验证:
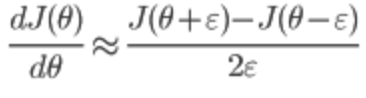
求出来的数值梯度应该与BP求出的梯度非常接近
验证BP正确后就不需要再执行验证梯度的算法了
代码实现
1 # 检验梯度是否计算正确 2 # 检验梯度是否计算正确 3 def checkGradient(Lambda = 0): 4 '''构造一个小型的神经网络验证,因为数值法计算梯度很浪费时间,而且验证正确后之后就不再需要验证了''' 5 input_layer_size = 3 6 hidden_layer_size = 5 7 num_labels = 3 8 m = 5 9 initial_Theta1 = debugInitializeWeights(input_layer_size,hidden_layer_size); 10 initial_Theta2 = debugInitializeWeights(hidden_layer_size,num_labels) 11 X = debugInitializeWeights(input_layer_size-1,m) 12 y = 1+np.transpose(np.mod(np.arange(1,m+1), num_labels))# 初始化y 13 14 y = y.reshape(-1,1) 15 nn_params = np.vstack((initial_Theta1.reshape(-1,1),initial_Theta2.reshape(-1,1))) #展开theta 16 '''BP求出梯度''' 17 grad = nnGradient(nn_params, input_layer_size, hidden_layer_size, 18 num_labels, X, y, Lambda) 19 '''使用数值法计算梯度''' 20 num_grad = np.zeros((nn_params.shape[0])) 21 step = np.zeros((nn_params.shape[0])) 22 e = 1e-4 23 for i in range(nn_params.shape[0]): 24 step[i] = e 25 loss1 = nnCostFunction(nn_params-step.reshape(-1,1), input_layer_size, hidden_layer_size, 26 num_labels, X, y, 27 Lambda) 28 loss2 = nnCostFunction(nn_params+step.reshape(-1,1), input_layer_size, hidden_layer_size, 29 num_labels, X, y, 30 Lambda) 31 num_grad[i] = (loss2-loss1)/(2*e) 32 step[i]=0 33 # 显示两列比较 34 res = np.hstack((num_grad.reshape(-1,1),grad.reshape(-1,1))) 35 print res
7、权重的随机初始化
神经网络不能像逻辑回归那样初始化theta为0,因为若是每条边的权重都为0,每个神经元都是相同的输出,在反向传播中也会得到同样的梯度,最终只会预测一种结果。
所以应该初始化为接近0的数
代码实现
1 # 随机初始化权重theta 2 def randInitializeWeights(L_in,L_out): 3 W = np.zeros((L_out,1+L_in)) # 对应theta的权重 4 epsilon_init = (6.0/(L_out+L_in))**0.5 5 W = np.random.rand(L_out,1+L_in)*2*epsilon_init-epsilon_init # np.random.rand(L_out,1+L_in)产生L_out*(1+L_in)大小的随机矩阵 6 return W
8、预测
正向传播预测结果
代码实现
1 # 预测 2 def predict(Theta1,Theta2,X): 3 m = X.shape[0] 4 num_labels = Theta2.shape[0] 5 #p = np.zeros((m,1)) 6 '''正向传播,预测结果''' 7 X = np.hstack((np.ones((m,1)),X)) 8 h1 = sigmoid(np.dot(X,np.transpose(Theta1))) 9 h1 = np.hstack((np.ones((m,1)),h1)) 10 h2 = sigmoid(np.dot(h1,np.transpose(Theta2))) 11 12 ''' 13 返回h中每一行最大值所在的列号 14 - np.max(h, axis=1)返回h中每一行的最大值(是某个数字的最大概率) 15 - 最后where找到的最大概率所在的列号(列号即是对应的数字) 16 ''' 17 #np.savetxt("h2.csv",h2,delimiter=',') 18 p = np.array(np.where(h2[0,:] == np.max(h2, axis=1)[0])) 19 for i in np.arange(1, m): 20 t = np.array(np.where(h2[i,:] == np.max(h2, axis=1)[i])) 21 p = np.vstack((p,t)) 22 return p
9、输出结果
梯度检查

随机显示100个手写数字

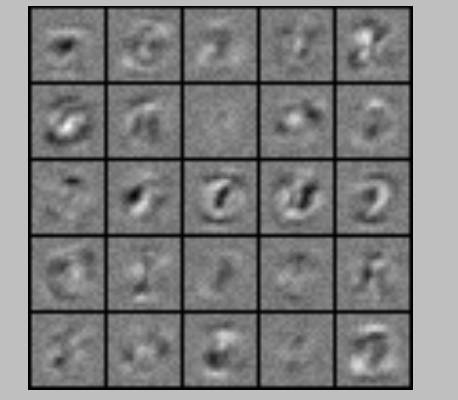
显示theta1权重
训练集预测准确度
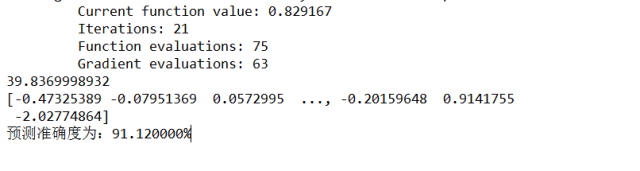
归一化后训练集预测准确度





 浙公网安备 33010602011771号
浙公网安备 33010602011771号