背景介绍
在最近的车载设备项目中,交通部808协议中有一个功能是判断当前车辆是否行驶在多边形区域中,如果超出区域需要进行报警。这里的位置是通过GPS实时获得。实际上这是一个判断点是否在多边形内的一个典型应用。
808协议描述:
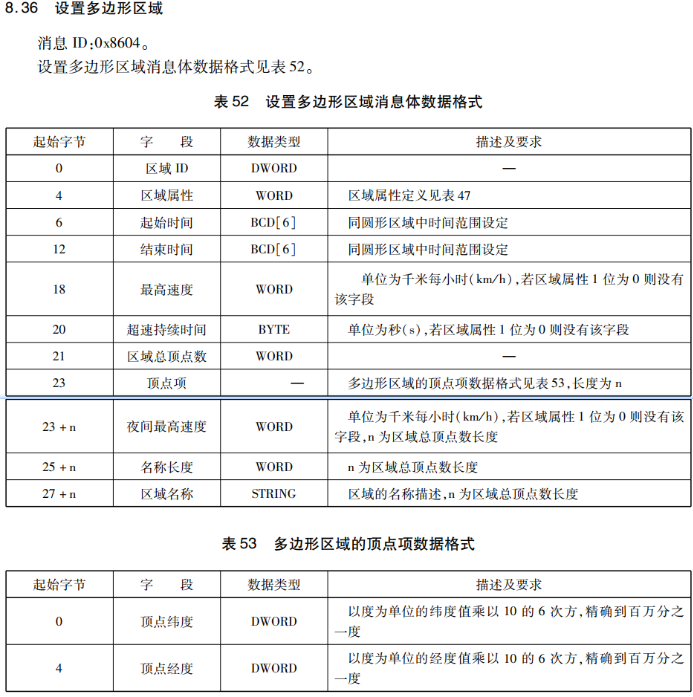
解法1: 射线法
由于此场景只需要判断单点是否在区域内,可以使用经典的射线法,此算法不需考虑精度误差和多边形点给出的顺序。算法复杂度为O(N)
此算法的思路是:
从检测点引一条射线,查看射线和多边形所有边的交点数目,如果左边和右边的交点数均为奇数,则检测点在多边形内; 如果左右两边的交点数均为偶数,则检测点在多边形外。
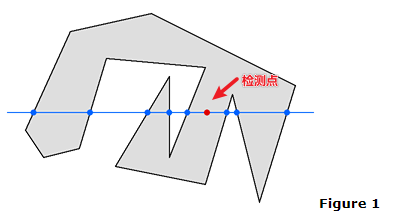
在图1中,射线左边有5个交点,右边有3个交点,故检测点在多边形内。
特别的,存在以下几种特殊情况:
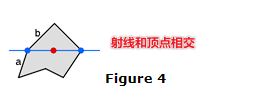

为了处理这些特殊情况,我们定义相交点肯定落在射线的上方,所以图4中边a 会产生一个交点,因为它的一个端点在射线上面,另一个在下边,而边b 不会产生交点,因为根据定义,它的两个端点都在射线上方,不算相交。
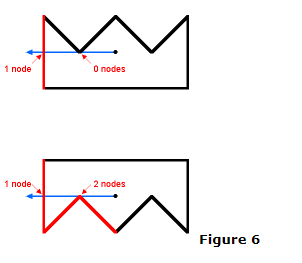
图5中,边c会产生一个交点,边d, e都不会产生交点。图6的情况类似。
另外,测试点刚好落在边上的情况需要单独讨论。
测试
为了测试代码的正确性,可以直接使用 HDU 1756 Cupid's Arrow 或者 Hrbust 1429 凸多边形
HDU 1756 注意坐标点要定义为double, 否则无法AC
点击查看代码
import java.io.IOException;
import java.util.Scanner;
public class HDU1756 { // OJ提交的时候要改成Main
private static double eps = 1e-6;
private static Point[] polygons; // 存储多边形顶点集
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int n = sc.nextInt(); // 多边形顶点数
polygons = new Point[n];
for (int i = 0; i < n; i++) {
double x = sc.nextDouble();
double y = sc.nextDouble();
polygons[i] = new Point(x, y);
}
n = sc.nextInt(); // 待测试点个数
for (int i = 0; i < n; i++) {
double x = sc.nextDouble();
double y = sc.nextDouble();
if (isInPolygon(new Point(x, y))) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
}
private static int dcmp(double x) {
if (Math.abs(x) < eps) {
return 0;
}
return x < 0 ? -1 : 1;
}
/**
* 判断点P是否在A,B所在的边上
*/
private static boolean onSegment(Point P, Point A, Point B) {
double crossRet = new Point(A.minus(P)).crossMulti(B.minus(P));
double dotRet = new Point(A.minus(P)).dotMulti(B.minus(P));
// 判断P在A,B所在直线上 以及 判断P在AB 范围内
return dcmp(crossRet) == 0 && dcmp(dotRet) <= 0;
}
private static boolean isInPolygon(Point q) {
boolean flag = false;
if (polygons.length == 0) return flag;
int n = polygons.length;
int j = n - 1;
for (int i = 0; i < n; i++) {
Point p1 = polygons[i];
Point p2 = polygons[j];
if (onSegment(q, p1, p2)) { // 测试点Q在边上
return true;
}
double x = q.x;
double y = q.y;
// 280ms
if (p1.y < y && p2.y >= y || p2.y < y && p1.y >= y) {
if (p1.x + (y - p1.y) / (p2.y - p1.y) * (p2.x - p1.x) < x) {
flag = !flag;
}
}
// 312 ms
// double slope;
// if (p2.x - p1.x == 0) {
// slope = 0;
// } else {
// slope = (p2.y - p1.y) / (p2.x - p1.x);
// }
//
// boolean cond1 = (p1.x <= x) && (x < p2.x);
// boolean cond2 = (p2.x <= x) && (x < p1.x);
// boolean above = (y < slope * (x - p1.x) + p1.y);
//
// if ((cond1 || cond2) && above) {
// flag = !flag;
// }
j = i;
}
return flag;
}
static class Point {
private double x, y;
public Point(double x, double y) {
this.x = x;
this.y = y;
}
public Point(Point p) {
this.x = p.x;
this.y = p.y;
}
private Point minus(Point p) {
return new Point(x - p.x, y - p.y);
}
private double dotMulti(Point p) {
return x * p.x + y * p.y;
}
private double crossMulti(Point p) {
return x * p.y - y * p.x;
}
}
}
两条直线是否相交的推导:

解法2: 二分法
算法思想:
1、选择多边形其中一个点O为起点,向多边形的其他顶点做射线
2、判断测试点是否在所有射线所包围的区域内。 如果点在最左侧向量左侧或最右侧向量右侧,则不在多边形内
3、用二分法找到点在哪两条向量之间,也就是找出点所在的大体区域
4、用两条向量v1, v2之间的顶点所形成的边a来判断测试点是否在多边形内
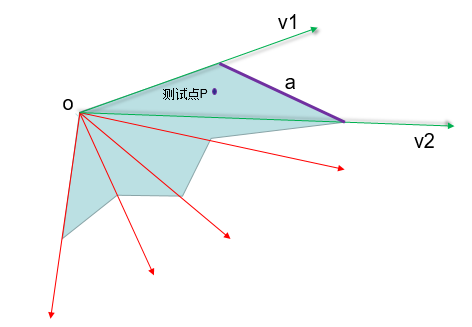
复杂度为O(logN)
使用下面的代码HDU 1756一直过不了,暂时不清楚问题在哪,这个OJ不好的地方就是没给出错误用例. Hrbust又注册不了。
点击查看代码
import java.io.IOException;
import java.util.Scanner;
public class Main {
private static double eps = 1e-6;
private static Point[] polygons; // 存储多边形顶点集
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
int n = sc.nextInt(); // 多边形顶点数
polygons = new Point[n];
for (int i = 0; i < n; i++) {
double x = sc.nextDouble();
double y = sc.nextDouble();
polygons[i] = new Point(x, y);
}
n = sc.nextInt(); // 待测试点个数
for (int i = 0; i < n; i++) {
double x = sc.nextDouble();
double y = sc.nextDouble();
if (isInPolygon(new Point(x, y))) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
}
}
private static int dcmp(double x) {
if (Math.abs(x) < eps) {
return 0;
}
return x < 0 ? -1 : 1;
}
/**
* 判断点P是否在A,B所在的边上
*/
private static boolean onSegment(Point P, Point A, Point B) {
double crossRet = new Point(A.minus(P)).crossMulti(B.minus(P));
double dotRet = new Point(A.minus(P)).dotMulti(B.minus(P));
// 判断P在A,B所在直线上 ,并且判断P在AB 范围内
return dcmp(crossRet) == 0 && dcmp(dotRet) <= 0;
}
/**
* 判断P 是否在AB所在直线上, 计算叉乘 (A - P) ^ (B - P)
* @return 0 在直线上
*/
private static double cross(Point P, Point A, Point B) {
return new Point(A.minus(P)).crossMulti(B.minus(P));
}
private static boolean isInPolygon(Point q) {
if (polygons.length == 0) return false;
int n = polygons.length;
int j = n - 1;
for (int i = 0; i < n; i++) {
Point p1 = polygons[i];
Point p2 = polygons[j];
if (onSegment(q, p1, p2)) { // 测试点Q在边上
return true;
}
j = i;
/// 1、判断测试点是否在最外侧两条向量外面
// dcmp((polygon[n - 1]-polygon[0])^(Q-polygon[0]))<=0 || dcmp((polygon[1]-polygon[0])^(P-polygon[0])) >= 0
if (dcmp(polygons[n - 1].minus(polygons[0]).crossMulti(q.minus(polygons[0]))) <= 0 ||
dcmp(polygons[1].minus(polygons[0]).crossMulti(q.minus(polygons[0]))) >= 0) {
return false;
}
// 2、二分查找测试点在哪个三角形中
int low = 2, high = n;
while (low < high) {
int mid = (low + high + 1) >> 1;
// dcmp((polygon[mid]-polygon[1])^(P-polygon[1]))<=0
if (dcmp(polygons[mid - 1].minus(polygons[0]).crossMulti(q.minus(polygons[0]))) <= 0) {
low = mid;
} else {
high = mid - 1;
}
}
// 3、判断测试点是否在第三条边外部
// dcmp((polygon[l+1]-polygon[l])^(P-polygon[l]))>=0
if (dcmp(polygons[low].minus(polygons[low - 1]).crossMulti(q.minus(polygons[low - 1]))) >= 0) {
return false;
}
}
return true;
}
static class Point {
private double x, y;
public Point(double x, double y) {
this.x = x;
this.y = y;
}
public Point(Point p) {
this.x = p.x;
this.y = p.y;
}
private Point minus(Point p) {
return new Point(x - p.x, y - p.y);
}
private double dotMulti(Point p) {
return x * p.x + y * p.y;
}
private double crossMulti(Point p) { // p^q > 0, P在Q的顺时针方向; < 0, P在Q的逆时针方向; = 0, p,q共线,可能同向或反向
return x * p.y - y * p.x;
}
}
}
另外一种写法也是过不了
点击查看代码
private static boolean isInPolygon(Point q) {
if (polygons.length == 0) return false;
int n = polygons.length;
int j = n - 1;
for (int i = 0; i < n; i++) {
Point p1 = polygons[i];
Point p2 = polygons[j];
if (onSegment(q, p1, p2)) { // 测试点Q在边上
return true;
}
j = i;
// 1、判断测试点是否在最外侧两条向量外面
if (cross(polygons[0], polygons[1], q) >= 0 || cross(polygons[0], polygons[n - 1], q) <= 0) {
return false;
}
// 2、二分查找测试点在哪个三角形中
int low = 2, high = n - 1;
while (low < high) {
int mid = low + (high - low) / 2;
if (cross(polygons[0], polygons[mid], q) > 0) {
high = mid;
} else {
low = mid + 1;
}
}
// 3、判断测试点是否在第三条边外部
if (cross(polygons[low], polygons[low - 1], q) <= 0) {
return false;
}
}
return true;
}
具体原因等有时间再研究一下,如果哪位朋友看出哪里有问题,帮忙指出
参考
Point-In-Polygon Algorithm — Determining Whether A Point Is Inside A Complex Polygon
Point in polygon
详谈判断点在多边形内的七种方法
hrbust 1429:凸多边形(计算几何,判断点是否在多边形内,二分法)
ACM-计算几何之凸多边形——hrbust1429


