支持向量机（SVM）

支持向量机(SVM)本身是针对二分类问题提出的，而SVR（支持向量回归）是SVM（支持向量机）中的一个重要的应用分支。SVR回归与SVM分类的区别在于，SVR的样本点最终只有一类，它所寻求的最优超平面不是SVM那样使两类或多类样本点分的“最开”，而是使所有的样本点离着超平面的总偏差最小。

• SVM是要使到超平面最近的样本点的“距离”最大；
• SVR则是要使到超平面最远的样本点的“距离”最小。

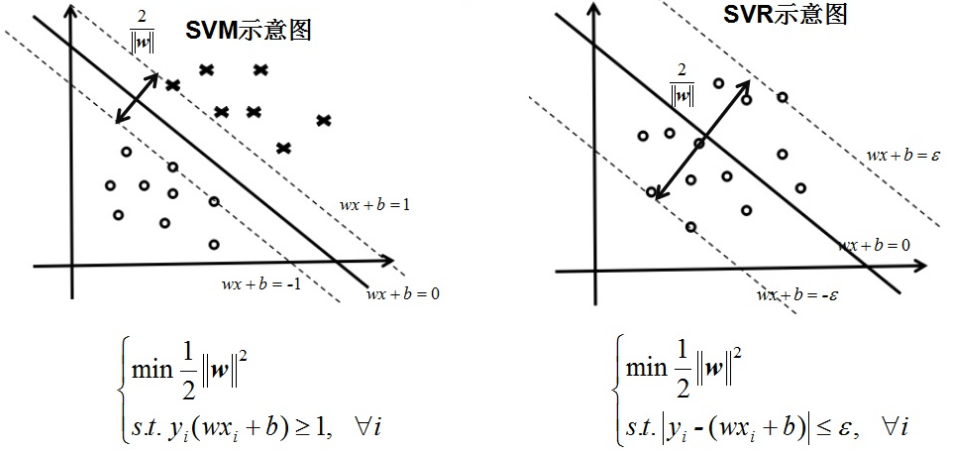
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　SVM/SVR图示

回归就像是寻找一堆数据的内在的关系。不论这堆数据有几种类别组成，得到一个公式，拟合这些数据，当给个新的坐标值时，能够求得一个新的值。所以对于SVR，就是求得一个面或者一个函数，可以把所有数据拟合了（就是指所有的数据点，不管属于哪一类，数据点到这个面或者函数的距离最近）

        统计上的理解就是：使得所有的数据的类内方差最小，把所有的类的数据看作是一个类。

        传统的回归方法当且仅当回归f(x)完全等于y时才认为是预测正确，需计算其损失；而支持向量回归(SVR)则认为只要是f(x)与y偏离程度不要太大，既可认为预测正确，不用计算损失。具体的就是设置一个阈值α，只是计算 |f(x) - y| > α 的数据点的loss。如图：支持向量回归表示只要在虚线内部的值都可认为是预测正确，只要计算虚线外部的值的损失即可。

　　　　

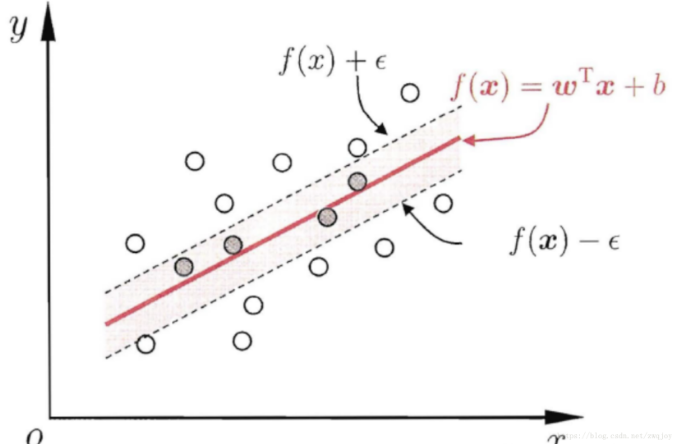
                                                                      SVR超平面