poj1418 Viva Confetti 判断圆是否可见

转载请注明出处： http://www.cnblogs.com/fraud/           ——by fraud

 

Viva Confetti

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 881		Accepted: 361

Description

Do you know confetti? They are small discs of colored paper, and people throw them around during parties or festivals. Since people throw lots of confetti, they may end up stacked one on another, so there may be hidden ones underneath. 

A handful of various sized confetti have been dropped on a table. Given their positions and sizes, can you tell us how many of them you can see? 

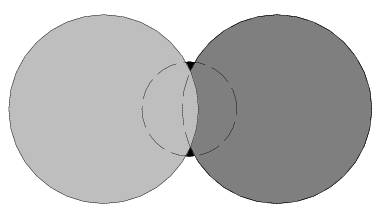
The following figure represents the disc configuration for the first sample input, where the bottom disc is still visible. 

Input

The input is composed of a number of configurations of the following form. 

n 
x1 y1 r1 
x2 y2 r2 
... 
xn yn rn 

The first line in a configuration is the number of discs in the configuration (a positive integer not more than 100), followed by one line descriptions of each disc : coordinates of its center and radius, expressed as real numbers in decimal notation, with up to 12 digits after the decimal point. The imprecision margin is +/- 5 x 10^(-13). That is, it is guaranteed that variations of less than +/- 5 x 10^(-13) on input values do not change which discs are visible. Coordinates of all points contained in discs are between -10 and 10. 

Confetti are listed in their stacking order, x1 y1 r1 being the bottom one and xn yn rn the top one. You are observing from the top. 

The end of the input is marked by a zero on a single line. 

Output

For each configuration you should output the number of visible confetti on a single line.

Sample Input

3
0 0 0.5
-0.9 0 1.00000000001
0.9 0 1.00000000001
5
0 1 0.5
1 1 1.00000000001
0 2 1.00000000001
-1 1 1.00000000001
0 -0.00001 1.00000000001
5
0 1 0.5
1 1 1.00000000001
0 2 1.00000000001
-1 1 1.00000000001
0 0 1.00000000001
2
0 0 1.0000001
0 0 1
2
0 0 1
0.00000001 0 1
0

Sample Output

3
5
4
2
2

依照顺序摆放下n个圆，问最终有多少个圆是可见的。

想了好久，然后问了队友shu_mj，想了好一会才想通。

首先，可见部分的一部分的边界一定是圆弧。于是，我们可以先求出所有的圆相交划分的一小段一小段的圆弧，然后把这些小段圆弧的中点稍微往圆内移动一点以及往外移动一点。然后从后放的圆开始判断，最先出现在哪个圆中，那么这个圆就是可见的。

/**
 * code generated by JHelper
 * More info: https://github.com/AlexeyDmitriev/JHelper
 * @author xyiyy @https://github.com/xyiyy
 */

#include <iostream>
#include <fstream>

//#####################
//Author:fraud
//Blog: http://www.cnblogs.com/fraud/
//#####################
//#pragma comment(linker, "/STACK:102400000,102400000")
#include <iostream>
#include <sstream>
#include <ios>
#include <iomanip>
#include <functional>
#include <algorithm>
#include <vector>
#include <string>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <set>
#include <map>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <climits>
#include <cctype>

using namespace std;
#define pb(X) push_back(X)
#define rep(X, N) for(int X=0;X<N;X++)
#define ALL(X) (X).begin(),(X).end()

//
// Created by xyiyy on 2015/8/10.
//

#ifndef JHELPER_EXAMPLE_PROJECT_P_HPP
#define JHELPER_EXAMPLE_PROJECT_P_HPP

const double EPS = 4e-13;

double add(double a, double b) {
    if (fabs(a + b) < EPS * (fabs(a) + fabs(b)))return 0;
    return a + b;
}

class P {
public:
    double x, y;

    P() { }

    P(double x, double y) : x(x), y(y) { }

    P  operator+(const P &p) {
        return P(add(x, p.x), add(y, p.y));
    }

    P operator-(const P &p) {
        return P(add(x, -p.x), add(y, -p.y));
    }

    P operator*(const double &d) {
        return P(x * d, y * d);
    }

    P operator/(const double &d) {
        return P(x / d, y / d);
    }

    double dot(P p) {
        return add(x * p.x, y * p.y);
    }


    double abs() {
        return sqrt(abs2());
    }

    double abs2() {
        return dot(*this);
    }

};



//求两圆的极角 以p为中心
double polarangle(P p, P q) {
    return atan2(q.y - p.y, q.x - p.x);
}


#endif //JHELPER_EXAMPLE_PROJECT_P_HPP

const long double PI2 = 2 * acos(-1.0);

long double update(double x) {
    while (x < 0.0)x += PI2;
    while (x >= PI2)x -= PI2;
    return x;
}

class poj1418 {
public:
    void solve(std::istream &in, std::ostream &out) {
        int n;
        P t;
        while (in >> n && n) {
            vector<P> ps;
            vector<double> rs;
            vector<bool> cansee(n, 0);
            rep(i, n) {
                double x, y, r;
                in >> x >> y >> r;
                ps.pb(P(x, y));
                rs.pb(r);
            }
            rep(i, n) {
                vector<double> pp;
                pp.pb(0.0);
                pp.pb(PI2);
                rep(j, n) {
                    double a = rs[i];
                    double d = (ps[i] - ps[j]).abs();
                    double b = rs[j];
                    if (a + b < d || a + d < b || b + d < a)continue;
                    double theta = acos((a * a + d * d - b * b) / (2 * a * d));
                    double alpha = polarangle(ps[i], ps[j]);
                    pp.pb(update(alpha - theta));
                    pp.pb(update(alpha + theta));
                }
                sort(ALL(pp));
                rep(j, pp.size() - 1) {
                    double theta = (pp[j] + pp[j + 1]) / 2;
                    for (int k = -1; k <= 1; k += 2) {
                        t.x = ps[i].x + (rs[i] + k * EPS) * cos(theta);
                        t.y = ps[i].y + (rs[i] + k * EPS) * sin(theta);
                        int gao = n - 1;
                        for (; gao >= 0; gao--) {
                            if ((ps[gao] - t).abs() < rs[gao])break;
                        }
                        if (gao != -1)cansee[gao] = 1;
                    }
                }
            }
            out << count(ALL(cansee), 1) << endl;
        }
    }
};

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    poj1418 solver;
    std::istream &in(std::cin);
    std::ostream &out(std::cout);
    solver.solve(in, out);
    return 0;
}