Codeforces Round #306 (Div. 2)

转载请注明出处： http://www.cnblogs.com/fraud/ ——by fraud

A. Two Substrings

You are given string s. Your task is to determine if the given string s contains two non-overlapping substrings "AB" and "BA" (the substrings can go in any order).

Input

The only line of input contains a string s of length between 1 and 10⁵ consisting of uppercase Latin letters.

Output

Print "YES" (without the quotes), if string s contains two non-overlapping substrings "AB" and "BA", and "NO" otherwise.

Sample test(s)

input

ABA

output

NO

input

BACFAB

output

YES

input

AXBYBXA

output

NO

Note

In the first sample test, despite the fact that there are substrings "AB" and "BA", their occurrences overlap, so the answer is "NO".

In the second sample test there are the following occurrences of the substrings: BACFAB.

In the third sample test there is no substring "AB" nor substring "BA".

暴力，不要重复覆盖即可

 1 #include <iostream>
 2 #include <sstream>
 3 #include <ios>
 4 #include <iomanip>
 5 #include <functional>
 6 #include <algorithm>
 7 #include <vector>
 8 #include <string>
 9 #include <list>
10 #include <queue>
11 #include <deque>
12 #include <stack>
13 #include <set>
14 #include <map>
15 #include <cstdio>
16 #include <cstdlib>
17 #include <cmath>
18 #include <cstring>
19 #include <climits>
20 #include <cctype>
21 using namespace std;
22 #define XINF INT_MAX
23 #define INF 0x3FFFFFFF
24 #define MP(X,Y) make_pair(X,Y)
25 #define PB(X) push_back(X)
26 #define REP(X,N) for(int X=0;X<N;X++)
27 #define REP2(X,L,R) for(int X=L;X<=R;X++)
28 #define DEP(X,R,L) for(int X=R;X>=L;X--)
29 #define CLR(A,X) memset(A,X,sizeof(A))
30 #define IT iterator
31 typedef long long ll;
32 typedef pair<int,int> PII;
33 typedef vector<PII> VII;
34 typedef vector<int> VI;
35 bool vis[100010];
36 string s;
37 vector<int>a,b;
38 int main()
39 {
40     ios::sync_with_stdio(false);
41     cin>>s;
42     int len=s.length();
43     for(int i=0;i<len-1;i++){
44         if(s[i]=='A'&&s[i+1]=='B'){
45             a.PB(i);
46         }
47     }
48     bool flag=0;
49     for(int i=0;i<len-1;i++){
50         if(s[i]=='B'&&s[i+1]=='A')
51             b.PB(i);
52     }
53     for(int i=0;i<a.size()&&!flag;i++){
54         for(int j=0;j<b.size()&&!flag;j++){
55             if(abs(a[i]-b[j])!=1){
56                 flag=1;
57             }
58         }
59     }
60     if(flag)cout<<"YES"<<endl;
61     else cout<<"NO"<<endl;
62     return 0;
63 }

代码君

B. Preparing Olympiad

You have n problems. You have estimated the difficulty of the i-th one as integer c_i. Now you want to prepare a problemset for a contest, using some of the problems you've made.

A problemset for the contest must consist of at least two problems. You think that the total difficulty of the problems of the contest must be at least l and at most r. Also, you think that the difference between difficulties of the easiest and the hardest of the chosen problems must be at least x.

Find the number of ways to choose a problemset for the contest.

Input

The first line contains four integers n, l, r, x (1 ≤ n ≤ 15, 1 ≤ l ≤ r ≤ 10⁹, 1 ≤ x ≤ 10⁶) — the number of problems you have, the minimum and maximum value of total difficulty of the problemset and the minimum difference in difficulty between the hardest problem in the pack and the easiest one, respectively.

The second line contains n integers c₁, c₂, ..., c_n (1 ≤ c_i ≤ 10⁶) — the difficulty of each problem.

Output

Print the number of ways to choose a suitable problemset for the contest.

Sample test(s)

input

3 5 6 1
1 2 3

output

input

4 40 50 10
10 20 30 25

output

input

5 25 35 10
10 10 20 10 20

output

Note

In the first example two sets are suitable, one consisting of the second and third problem, another one consisting of all three problems.

In the second example, two sets of problems are suitable — the set of problems with difficulties 10 and 30 as well as the set of problems with difficulties 20 and 30.

In the third example any set consisting of one problem of difficulty 10 and one problem of difficulty 20 is suitable.

直接枚举所有情况即可

 1 #include <iostream>
 2 #include <sstream>
 3 #include <ios>
 4 #include <iomanip>
 5 #include <functional>
 6 #include <algorithm>
 7 #include <vector>
 8 #include <string>
 9 #include <list>
10 #include <queue>
11 #include <deque>
12 #include <stack>
13 #include <set>
14 #include <map>
15 #include <cstdio>
16 #include <cstdlib>
17 #include <cmath>
18 #include <cstring>
19 #include <climits>
20 #include <cctype>
21 using namespace std;
22 #define XINF INT_MAX
23 #define INF 0x3FFFFFFF
24 #define MP(X,Y) make_pair(X,Y)
25 #define PB(X) push_back(X)
26 #define REP(X,N) for(int X=0;X<N;X++)
27 #define REP2(X,L,R) for(int X=L;X<=R;X++)
28 #define DEP(X,R,L) for(int X=R;X>=L;X--)
29 #define CLR(A,X) memset(A,X,sizeof(A))
30 #define IT iterator
31 typedef long long ll;
32 typedef pair<int,int> PII;
33 typedef vector<PII> VII;
34 typedef vector<int> VI;
35 int a[1010];
36 int b[1010];
37 int main()
38 {
39     ios::sync_with_stdio(false);
40     int n,l,r,x;
41     cin>>n>>l>>r>>x;
42     for(int i=0;i<n;i++){
43         cin>>a[i];
44     }
45     int ans=0;
46     int tot=(1<<n);
47     for(int i=0;i<tot;i++){
48         int cnt=0;
49         int gao=0;
50         int minn=2000000000;
51         int maxx =0;
52         for(int j=0;j<n;j++){
53             if((1<<j)&i){
54                 cnt++;
55                 gao+=a[j];
56                 minn=min(a[j],minn);
57                 maxx= max(a[j],maxx);
58             }
59         }
60         if(gao>=l&&gao<=r&&cnt>=2&&maxx-minn>=x){
61             ans++;
62         }
63 
64     }
65     cout<<ans<<endl;
66     return 0;
67 }

代码君

C. Divisibility by Eight

You are given a non-negative integer n, its decimal representation consists of at most 100 digits and doesn't contain leading zeroes.

Your task is to determine if it is possible in this case to remove some of the digits (possibly not remove any digit at all) so that the result contains at least one digit, forms a non-negative integer, doesn't have leading zeroes and is divisible by 8. After the removing, it is forbidden to rearrange the digits.

If a solution exists, you should print it.

Input

The single line of the input contains a non-negative integer n. The representation of number n doesn't contain any leading zeroes and its length doesn't exceed 100 digits.

Output

Print "NO" (without quotes), if there is no such way to remove some digits from number n.

Otherwise, print "YES" in the first line and the resulting number after removing digits from number n in the second line. The printed number must be divisible by 8.

If there are multiple possible answers, you may print any of them.

Sample test(s)

input

output

YES
344

input

output

YES
0

input

output

NO

问能否去掉一些数字，是的最终的这个数能被8整除。

找出能够被8整除的1000以内的数，然后依次判断是否满足即可。

 1 #include <iostream>
 2 #include <sstream>
 3 #include <ios>
 4 #include <iomanip>
 5 #include <functional>
 6 #include <algorithm>
 7 #include <vector>
 8 #include <string>
 9 #include <list>
10 #include <queue>
11 #include <deque>
12 #include <stack>
13 #include <set>
14 #include <map>
15 #include <cstdio>
16 #include <cstdlib>
17 #include <cmath>
18 #include <cstring>
19 #include <climits>
20 #include <cctype>
21 using namespace std;
22 #define XINF INT_MAX
23 #define INF 0x3FFFFFFF
24 #define MP(X,Y) make_pair(X,Y)
25 #define PB(X) push_back(X)
26 #define REP(X,N) for(int X=0;X<N;X++)
27 #define REP2(X,L,R) for(int X=L;X<=R;X++)
28 #define DEP(X,R,L) for(int X=R;X>=L;X--)
29 #define CLR(A,X) memset(A,X,sizeof(A))
30 #define IT iterator
31 typedef long long ll;
32 typedef pair<int,int> PII;
33 typedef vector<PII> VII;
34 typedef vector<int> VI;
35 string str[130]={"0","8","16","24","32","40","48","56","64","72","80","88","96","104","112","120","128","136","144","152","160","168","176","184","192","200",
36 "208","216","224","232","240","248","256","264","272","280","288","296","304","312","320","328","336","344","352","360","368","376","384","392","400",
37 "408","416","424","432","440","448","456","464","472","480","488","496","504","512","520","528","536","544","552","560","568","576","584","592","600",
38 "608","616","624","632","640","648","656","664","672","680","688","696","704","712","720","728","736","744","752","760","768","776","784","792","800",
39 "808","816","824","832","840","848","856","864","872","880","888","896","904","912","920","928","936","944","952","960","968","976","984","992","1000"
40 };
41 int main()
42 {
43     ios::sync_with_stdio(false);
44     string s;
45     cin>>s;
46     int len =s.length();
47     string ans;
48     bool flag=0;
49     for(int i=0;i<125;i++){
50         int len2=str[i].length();
51         int j=len2-1;
52         for(int k=len-1;k>=0;k--){
53             if(s[k]==str[i][j]){
54                 j--;
55             }
56             if(j<0){
57                 flag=1;
58             }
59         }
60         if(flag){
61             ans=str[i];
62             break;
63         }
64     }
65     if(flag){
66         cout<<"YES"<<endl;
67         cout<<ans<<endl;
68     }
69     else cout<<"NO"<<endl;
70 
71     return 0;
72 }

代码君

D. Regular Bridge

An undirected graph is called k-regular, if the degrees of all its vertices are equal k. An edge of a connected graph is called a bridge, if after removing it the graph is being split into two connected components.

Build a connected undirected k-regular graph containing at least one bridge, or else state that such graph doesn't exist.

Input

The single line of the input contains integer k (1 ≤ k ≤ 100) — the required degree of the vertices of the regular graph.

Output

Print "NO" (without quotes), if such graph doesn't exist.

Otherwise, print "YES" in the first line and the description of any suitable graph in the next lines.

The description of the made graph must start with numbers n and m — the number of vertices and edges respectively.

Each of the next m lines must contain two integers, a and b (1 ≤ a, b ≤ n, a ≠ b), that mean that there is an edge connecting the vertices a and b. A graph shouldn't contain multiple edges and edges that lead from a vertex to itself. A graph must be connected, the degrees of all vertices of the graph must be equal k. At least one edge of the graph must be a bridge. You can print the edges of the graph in any order. You can print the ends of each edge in any order.

The constructed graph must contain at most 10⁶ vertices and 10⁶ edges (it is guaranteed that if at least one graph that meets the requirements exists, then there also exists the graph with at most 10⁶ vertices and at most 10⁶ edges).

Sample test(s)

input

output

YES
2 1
1 2

Note

In the sample from the statement there is a suitable graph consisting of two vertices, connected by a single edge.

问没否构成一张有割边的无向图，且图中的每个点的度数都为k度

首先偶数不能构成。

其次，我们先构造割边一端的情况，然后剩下一半，复制一下即可。

先取k个点，两两相连，那个每个点的度数都为k-1,由于有一点是割边上的点，那么，也就是，我们要是的另外的k-1个点的度数变成k。

我们可以发现，每两个这k-1个点中的点，可以和由k+1个点构成的完全图去掉一条边的图相结合，从而变成k度点。由此，可以全部构建。

 1 #include <iostream>
 2 #include <sstream>
 3 #include <ios>
 4 #include <iomanip>
 5 #include <functional>
 6 #include <algorithm>
 7 #include <vector>
 8 #include <string>
 9 #include <list>
10 #include <queue>
11 #include <deque>
12 #include <stack>
13 #include <set>
14 #include <map>
15 #include <cstdio>
16 #include <cstdlib>
17 #include <cmath>
18 #include <cstring>
19 #include <climits>
20 #include <cctype>
21 using namespace std;
22 #define XINF INT_MAX
23 #define INF 0x3FFFFFFF
24 #define MP(X,Y) make_pair(X,Y)
25 #define PB(X) push_back(X)
26 #define REP(X,N) for(int X=0;X<N;X++)
27 #define REP2(X,L,R) for(int X=L;X<=R;X++)
28 #define DEP(X,R,L) for(int X=R;X>=L;X--)
29 #define CLR(A,X) memset(A,X,sizeof(A))
30 #define IT iterator
31 typedef long long ll;
32 typedef pair<int,int> PII;
33 typedef vector<PII> VII;
34 typedef vector<int> VI;
35 vector<int>G[10010];
36 int tot=0;
37 void add_edge(int u,int v){
38     G[u].PB(v);
39     tot++;
40 }
41 int main()
42 {
43     ios::sync_with_stdio(false);
44     int k;
45     cin>>k;
46     if(k==1){
47         cout<<"YES"<<endl;
48         cout<<"2 1"<<endl;
49         cout<<"1 2"<<endl;
50         return 0;
51     }
52     if(k%2==0){
53         cout<<"NO"<<endl;
54         return 0;
55     }
56     for(int i=1;i<=k-1;i++){
57         for(int j=i+1;j<=k;j++){
58             add_edge(i,j);
59         }
60     }
61     int j=k;
62     for(int i=3;i<=k;i+=2,j+=k+1){
63         for(int s=j+1;s<j+k;s++){
64             for(int t=s+1;t<=j+k+1;t++){
65                 add_edge(s,t);
66             }
67         }
68         add_edge(i-1,j+k);
69         add_edge(i,j+k+1);
70     }
71     j = (k-1)/2*(k+1)+k;
72     for(int i=j+1;i<=j+k-1;i++){
73         for(int s=i+1;s<=j+k;s++){
74             add_edge(i,s);
75         }
76     }
77     int temp = j;
78     j+=k;
79     for(int i=temp+3;i<=temp+k;i+=2,j+=k+1){
80         for(int s=j+1;s<j+k;s++){
81             for(int t=s+1;t<=j+k+1;t++){
82                 add_edge(s,t);
83             }
84         }
85         add_edge(i-1,j+k);
86         add_edge(i,j+k+1);
87     }
88     add_edge(1,temp+1);
89     printf("YES\n");
90     printf("%d %d\n",((k-1)/2*(k+1)+k)*2,tot);
91     for(int i=1;i<=((k-1)/2*(k+1)+k)*2;i++){
92         for(int j=0;j<G[i].size();j++){
93             printf("%d %d\n",i,G[i][j]);
94         }
95     }
96     return 0;
97 }

E. Brackets in Implications

Implication is a function of two logical arguments, its value is false if and only if the value of the first argument is true and the value of the second argument is false.

Implication is written by using character ' $\text{[math]}$ ', and the arguments and the result of the implication are written as '0' (false) and '1' (true). According to the definition of the implication:

$\text{[math]}$

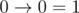
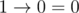
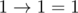
When a logical expression contains multiple implications, then when there are no brackets, it will be calculated from left to fight. For example,

$\text{[math]}$ .

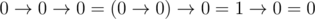When there are brackets, we first calculate the expression in brackets. For example,

$\text{[math]}$ .

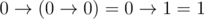For the given logical expression 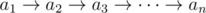$\text{[math]}$ determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.

Input

The first line contains integer n (1 ≤ n ≤ 100 000) — the number of arguments in a logical expression.

The second line contains n numbers a₁, a₂, ..., a_n (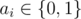 $\text{[math]}$ ), which means the values of arguments in the expression in the order they occur.

Output

Print "NO" (without the quotes), if it is impossible to place brackets in the expression so that its value was equal to 0.

Otherwise, print "YES" in the first line and the logical expression with the required arrangement of brackets in the second line.

The expression should only contain characters '0', '1', '-' (character with ASCII code 45), '>' (character with ASCII code 62), '(' and ')'. Characters '-' and '>' can occur in an expression only paired like that: ("->") and represent implication. The total number of logical arguments (i.e. digits '0' and '1') in the expression must be equal to n. The order in which the digits follow in the expression from left to right must coincide with a₁, a₂, ..., a_n.

The expression should be correct. More formally, a correct expression is determined as follows:

Expressions "0", "1" (without the quotes) are correct.
If v₁, v₂ are correct, then v₁->v₂ is a correct expression.
If v is a correct expression, then (v) is a correct expression.

The total number of characters in the resulting expression mustn't exceed 10⁶.

If there are multiple possible answers, you are allowed to print any of them.

Sample test(s)

input

4
0 1 1 0

output

YES
(((0)->1)->(1->0))

input

2
1 1

output

NO

input

1
0

output

YES
0

首先，最后以为必须要是0，否则为NO

另外，序列中，偶数个连续的0，可以通过两两结合，变成全是1的序列。奇数个连续的0，也是两两结合（优先结合后两个，留下第一个）变成一个011……11的序列。

然后需要特殊考虑序列的最后两位都为0的情况。

  1 #include <iostream>
  2 #include <sstream>
  3 #include <ios>
  4 #include <iomanip>
  5 #include <functional>
  6 #include <algorithm>
  7 #include <vector>
  8 #include <string>
  9 #include <list>
 10 #include <queue>
 11 #include <deque>
 12 #include <stack>
 13 #include <set>
 14 #include <map>
 15 #include <cstdio>
 16 #include <cstdlib>
 17 #include <cmath>
 18 #include <cstring>
 19 #include <climits>
 20 #include <cctype>
 21 using namespace std;
 22 #define XINF INT_MAX
 23 #define INF 0x3FFFFFFF
 24 #define MP(X,Y) make_pair(X,Y)
 25 #define PB(X) push_back(X)
 26 #define REP(X,N) for(int X=0;X<N;X++)
 27 #define REP2(X,L,R) for(int X=L;X<=R;X++)
 28 #define DEP(X,R,L) for(int X=R;X>=L;X--)
 29 #define CLR(A,X) memset(A,X,sizeof(A))
 30 #define IT iterator
 31 typedef long long ll;
 32 typedef pair<int,int> PII;
 33 typedef vector<PII> VII;
 34 typedef vector<int> VI;
 35 bool a[100010];
 36 bool cal(int x,int y){
 37     if(x==0)return 1;
 38     if(y==1)return 1;
 39     return 0;
 40 }
 41 int main()
 42 {
 43     ios::sync_with_stdio(false);
 44     int n;
 45     cin>>n;
 46     for(int i=0;i<n;i++){
 47         cin>>a[i];
 48     }
 49 
 50     if(a[n-1]!=0){
 51         cout<<"NO"<<endl;
 52         return 0;
 53     }
 54     if(n>=2&&a[n-2]==0&&a[n-1]==0){
 55         bool f=0;
 56         for(int i=0;i<n-2;i++){
 57             if(a[i]==0)f=1;
 58         }
 59         if(f){
 60             cout<<"YES"<<endl;
 61             int m=1;
 62             int j=n-3;
 63             for(int i=n-3;i>=0;i--,j--){
 64                 if(a[i]==0)break;
 65                 m++;
 66             }
 67             for(int i=0;i<j;i++){
 68                 if(a[i]==1){
 69                     cout<<"1->";
 70                 }
 71                 else{
 72                     int num=1;
 73                     while(a[i+1]==0&&i+1<j){
 74                         num++;
 75                         i++;
 76                     }
 77                     if(num&1){
 78                         cout<<0<<"->";
 79                         num--;
 80                     }
 81                     while(num){
 82                         cout<<"(0->0)->";
 83                         num-=2;
 84                     }
 85 
 86                 }
 87             }
 88 
 89             for(int i=j;i<n-1;i++){
 90                 if(i!=n-2)cout<<"(";
 91                 cout<<a[i];
 92                 if(i==n-2){
 93                     for(int k=0;k<m;k++){
 94                         cout<<")";
 95                     }
 96                 }
 97                 cout<<"->";
 98             }
 99             cout<<0<<endl;
100         }else{
101             cout<<"NO"<<endl;
102         }
103         return 0;
104     }
105     //=================
106     cout<<"YES"<<endl;
107     for(int i=0;i<n-1;i++){
108         if(a[i]==1){
109             cout<<"1->";
110         }
111         else{
112             int num=1;
113             while(a[i+1]==0&&i+1<n-1){
114                 num++;
115                 i++;
116             }
117             if(num&1){
118                 cout<<0<<"->";
119                 num--;
120             }
121             while(num){
122                 cout<<"(0->0)->";
123                 num-=2;
124             }
125 
126         }
127     }
128     cout<<0<<endl;
129     return 0;
130 }

posted on 2015-06-05 03:47 xyiyy 阅读(239) 评论(0) 编辑收藏举报

刷新页面返回顶部

Codeforces Round #306 (Div. 2)

导航

公告