[hdu5136]Yue Fei's Battle 2014 亚洲区域赛广州赛区J题(dp)

转载请注明出处： http://www.cnblogs.com/fraud/           ——by fraud

 

现场赛的时候由于有个地方有点小问题，没有成功AC，导致与金牌失之交臂。

---

 

由于今天下午有点事情，无法打重现，所以下午只是花了十分钟做了一道J题，抢了个FB，2333333333

Yue Fei's Battle

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 15    Accepted Submission(s): 3

Problem Description

Yue Fei is one of the most famous military general in Chinese history.He led Southern Song army in the wars against the Jin dynasty of northern China. Yue Fei achieved a lot of victory and hopefully could retake Kaifeng ,the former capital of Song occupied by Jin. Fearing that retaking Kaifeng might cause the Jin to release former Emperor Song Qinzong, threatening his throne, Emperor Song Gaozong took some corrupted officers' advice, sending 12 urgent orders in the form of 12 gold plaques to Yue Fei, recalling him back to the capital.

Then Yue Fei was put into prison and was killed under a charge of "maybe there is" treason. But later Yue Fei was posthumously pardoned and rehabilitated, and became a symbol of loyalty to the country. The four corrupted officers who set him up were Qin Hui,Qin Hui's wife Lady Wang, Moqi Xie and Zhang Jun. People made kneeling iron statues of them and put the statues before Yue Fei's tomb (located by the West Lake, Hangzhou). For centuries, these statues have been cursed, spat and urinated upon by people. (Now please don't do that if you go to Hangzhou and see the statues.)

One of the most important battle Yue Fei won is the battle in Zhuxian town. In Zhuxian town, Yue Fei wanted to deploy some barracks, and connected those barracks with roads. Yue Fei needed all the barracks to be connected, and in order to save money, he wanted to build as less roads as possible. There couldn't be a barrack which is too important, or else it would be attacked by enemies. So Yue Fei required that NO barrack could connect with more than 3 roads. According to his battle theory, Yue Fei also required that the length of the longest route among the barracks is exactly K. Note that the length of a route is defined as the number of barracks lied on it and there may be several longest routes with the same length K.

Yue Fei wanted to know, in how many different ways could he deploy the barracks and roads. All barracks could be considered as no different. Yue Fei could deploy as many barracks as he wanted.

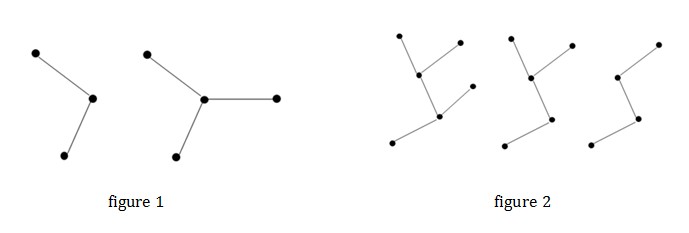
For example, if K is 3,Yue Fei had 2 ways to deploy the barracks and roads as shown in figure1. If K is 4, the 3 kinds of layouts is shown in figure 2. (Thick dots stand for barracks, and segments stand for roads):


Please bring your computer and go back to Yue Fei's time to help him so that you may change the history.

 

 

Input

The input consists of no more than 25 test cases.

For each test, there is only one line containing a integer K(1<=K<=100,000) denoting the length of the longest route.

The input ends by K = 0.

 

 

Output

For each test case, print an integer denoting the number of different ways modulo 1000000007.

 

 

Sample Input

3

4

0

 

 

Sample Output

2

3

 

题意：规定每个结点最多连3个点，有若干个结点构成一棵树，则在树的直径为k时，共有几种非同构的结构。

分析：由于需要考虑非同构的情况比较复杂，那么，我们可以考虑将这棵树拆开，先看偶数，偶数比较简单

1.若直径n为偶数，则选取这棵树的直径的中间那条边，将其断开，从而产生长度均为n/2的两个分支，为了保证计数时不会将同构的重复计入，根据组合数学，则方案数为C(num[n/2]+2-1，2)；

注：num[i]表示分支长度为i的非同构的种数。

　　dp[i]表示分支长度从0到i的所有非同构的分支方案数。

2.若直径n为奇数，则选取这棵树的直径上的中点，从而拆分成长度为(n-1)/2，长度为(n-1)/2以及另一条长度可为0到(n-1)/2的三个分支。

　　a.若剩下一条分支的长度为[0,(n-1)/2-1]，根据组合数学，可以得到对应的方案数为dp[(n-1)/2-1]*C(num[(n-1)/2]+2-1,2);

　　b.若剩下另一条分支的长度也为(n-1)/2，则此情况下对应的方案数为C(num[(n-1)/2]+3-1,3);

　　即奇数情况为dp[(n-1)/2-1]*C(num[(n-1)/2]+2-1,2)+C(num[(n-1)/2]+3-1,3);

接下来考虑num[i]与dp[i]是如何得出的问题：

显然dp[i]只是一个前缀和，求出num[i]之后累加即可。

对于num[i]，对于长度为i的分支，其端点上只能连接两个子分支（因为另一个要留着与其它分支相连），那么，对于长度为i+1的分支，则只是在长度为i的分支的端点处，增加了一个结点，然后再在新的端点上添加长度为0到i的分支。

　　a.若添加的分支的长度为0到i-1，则方案数为num[i]*dp[i-1];

　　b.若添加的分支的长度为i，则方案数为C(num[i]+2-1,2);

　　即num[i+1]=num[i]*dp[i-1]+C(num[i]+2-1,2);

#include <iostream>
#include <sstream>
#include <ios>
#include <iomanip>
#include <functional>
#include <algorithm>
#include <vector>
#include <string>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <set>
#include <map>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <climits>
#include <cctype>
using namespace std;
#define XINF INT_MAX
#define INF 0x3FFFFFFF
#define MP(X,Y) make_pair(X,Y)
#define PB(X) push_back(X)
#define REP(X,N) for(int X=0;X<N;X++)
#define REP2(X,L,R) for(int X=L;X<=R;X++)
#define DEP(X,R,L) for(int X=R;X>=L;X--)
#define CLR(A,X) memset(A,X,sizeof(A))
#define IT iterator
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<PII> VII;
typedef vector<int> VI;
const int maxn=100010;
ll dp[maxn];
ll num[maxn];
const int mod=1000000007;
ll inv(int x)
{
    int n=mod-2;
    ll temp=x;
    ll ret=1;
    while(n)
    {
        if(n&1)ret=ret*temp%mod;
        temp=temp*temp%mod;
        n>>=1;
    }
    return ret;
}
int main()
{
    ios::sync_with_stdio(false);
    ll inv_2,inv_3;
    inv_2=inv(2);
    inv_3=inv(3);
    dp[0]=num[0]=1;
    dp[1]=num[1]=1;
    for(int i=2;i<maxn;i++)
    {
        dp[i]=(num[i-1]*dp[i-2]%mod+(num[i-1]+1)*num[i-1]%mod*inv_2%mod)%mod;
        dp[i-1]+=dp[i-2];
        dp[i-1]%=mod;
        num[i]=dp[i];
    }
    int n;
    while(cin>>n&&n)
    {
        ll ans; 
        if(n==1)ans=1;
        else if(n==2)ans=1;
        else if(n&1)
        {
            ans=num[n/2]*(num[n/2]+1)%mod*inv_2%mod*dp[n/2-1]%mod;
            ans+=num[n/2]*(num[n/2]+1)%mod*(num[n/2]+2)%mod*inv_2%mod*inv_3%mod;
            ans%=mod;
        }
        else 
        {
            ans=(num[n/2]*(num[n/2]+1))%mod*inv_2%mod;
        }
        cout<<ans<<endl;
    }
    return 0;
}