【Manacher算法】最长子回文串

【Manacher算法】

　　这个算法用来找出一个字符串中最长的回文子字符串。

　　如果采取暴力解最长回文子字符串问题，大概可以有两种思路：1. 遍历出所有子字符串找其中最长的回文 2. 从每个字符作为中心，向两边扩散看是否回文。 第二种比第一种稍微高明一点，但是总体的复杂度还是O(n^2)的。

　　而Manacher算法可以做到O(n)时间复杂度，O(n)空间复杂度。

■　　思路&描述

　　回文字符串有一个比较麻烦的地方，就是回文串有偶回文和奇回文两种，分别举例ABBA和ABCBA。这种区别可能要让我们在程序中额外伸出一个判断分支来，不是很方便。所以Manacher算法的第一步就是预处理字符串，将原先的字符串所有字符中间再加上头尾两端都加上一个特殊符号，这样就可以把所有可能的回文串都变成了奇回文串，方便处理：

　　如ABBA变成#A#B#B#A#，ABCBA变成#A#B#C#B#A#。此外，一般实践中为了保证边界上也能统一，还会额外在头上（理论上字符串尾也可以加，但是目前尾巴上肯定是#，大不了我们遍历的时候最后这轮以这个#字符为基础的遍历不去做了，这样就可以避免尾部边界出错）加上一个$或者其他有别于#的特殊符号表示字符串的开始。经过这样预处理之后的字符串可以拿来被manacher算法处理。

　　接下来，基本思路肯定还是要找出以每个字符为中心时，回文串最长可以做到多少。只是一个个去遍历太暴力了，这里可以借鉴一下动态规划中的一点小心思，也就是说我们能不能利用已有的信息（当然这部分信息是需要在之前的分析过程中手动保存下来的）来更加方便地推出我们未知的信息。

　　比如我们可以创建一个数组p，针对被加工过字符串s，p的长度被设定为和s等长，且p中保存的内容，是以对应原s字符串中那个字符为中心，其最大回文子字符串的半径长度。由于s中所有回文串都是奇回文串，所以我们所说的半径是指从回文串的左端开始到中心（算入中心）的长度。如#a#b#a#的半径是4，#a#b#b#a#的半径是5。

　　那么如何基于一些现有信息推断新的信息呢？考虑这样一种情形：假如我们以i变量作为向右遍历的下标，逐渐向右遍历确定了一个回文子串。这个子串的中心和半径两个参数都是可以明确的。不妨称中心的下标为id，称回文串最右端下标为mx（这也是后续编码过程中需要使用的两个辅助变量）。确定完id和mx之后我们继续往右推移i。

　　当我们来到一个新的i时，如果它还在mx范围内，此时可以注意到，其实存在一个点j，j和i关于id对称，由于id,mx的回文特性，所以j的回文串很大可能就是i的回文串。这种可能成为确定只需要一个条件，那就是p[j]的取值，没有超出id,mx这个回文串的范围。下面是盗来的图，说明了i,j,id,mx以及mx'（mx关于id的对称点）的布局。

　　

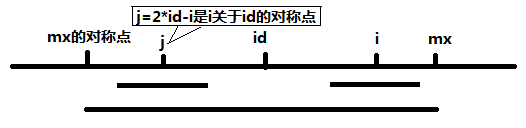
　　那么如果p[j] > j - mx'，即j对应的回文串已经超出了mx的范围，此时改怎么办？很显然，在mx'到j的这段内容，由于id,mx的回文性，还是可以对应到i到mx这段内容的。至于mx之后的内容，只能再去一个个字符遍历过去看能不能符合回文。

　　总的来说，当i仍然小于mx时，i的取值应该可以取min(p[j],mx-i)，当取p[j]的时候，p[i]就是p[j]的值。当取mx-i的时候，mx-i还只是一个基础值，还需要进一步处理来获得准确值。

　　还没有讨论完，刚才说的都是i<mx的情况，如果此时已经遍历到超过mx了怎么办？此时由于没有任何既存的回文串性质可以利用，所以只能老老实实向外一个个字符扩散判断回文性。比较好的一点是，之前讨论过的关于i<mx的两种取值可能，也都可以（或必要）做这个扩散。

　　为了保证递推的连续性，不论上上述哪种可能，获得到i的回文串之后，都需要将id和mx进行更新。应该注意，id和mx并不是我们最后要求的最长回文子串的属性，而只是当前已经遍历过的最靠右的一个回文子串的属性。

　　而要求最长回文子串的属性我们可以再维护一个类似于longestInfo之类的变量，每找出一个回文子串后判断它是不是最长的。所有循环结束后去这个变量里面取值就好了。

 

■　　编码实现

　　下面是manacher算法的python实现：

def longestPalindrome(s):
    """
    :type s: str
    :rtype: str
    """
    s = '$#' + '#'.join(list(s)) + '#'    # 预处理
    p = [0] * len(s)
    longestInfo = [0,0]
    i,currRes,currMax = 1,0,0  # 由于s[0]是$，所以i从1开始取值。id和mx分别换了个名字currRes和currMax
    while i < len(s):
        if i > currMax:    # i已经超出mx的情况
            p[i] = 1
        else:    # i未超出mx，再分成两种情况，体现在min函数中
            j = 2*currRes - i
            p[i] = min(p[j],currMax-i)
        # 此时p[i]并不一定已经正确，除了决定p[i]=p[j]，其他两个分支都只是给了p[i]一个基准值
        while i-p[i]>0 and i+p[i]<len(s) and s[i-p[i]] == s[i+p[i]]:
            # 进行一个个字符向外扩散的回文性检查
            # 注意为了防止越界访问，还要有边界判断条件
            p[i] += 1
        # 这时p[i]才得到了最终确定的值 接下来就是将其相关属性与已有的currRes和currMax比较，看是否需要更新
        if i + p[i] > currMax:
            # 更新id和max
            currRes = i
            currMax = i + p[i] - 1

        if p[i] > longestInfo[1]:
            # 更新最终结果值
            longestInfo = i,p[i]

        i += 1
    center = longestInfo[0]
    radius = longestInfo[1] - 1    # 注意，半径把对称中心本身算进去了，所以减一
    return s[center-radius:center+radius+1].replace('#','')  # 直接replace去掉所有辅助字符，得到的就是原字符串的结果了。