【Leetcode】收集
万事总要有个开头，来吧。
问题原题看情况，如果我能用中文准确地表述出来的话那就用中文说一下。也有可能完全不说…
■ twoSum
问题： 参数是一个数组nums和一个目标数target，寻找nums中两个数的和是target，返回这两个数的下标。同一个数不能重复使用。假设只有一个正确的解。
注意点： 由于同一个数不能重复使用，用掉一个数之后这个数就不能再计入使用范围。但同时也要注意[3,3] 6这种情况，即同一个数不能用两次，但是要考虑有两个相同值的数
朴素解法：
def sumTwo(nums,targets): for i in nums: idx_1 = nums.index(i) try: idx_2 = nums.index(target-i,idx_1+1) except ValueError,e: continue return [idx_1,idx_2]
这个解法比较好地利用了python里的切片机制，以及index方法的beg参数。不愧是python，代码简洁得一比。不过这种解法的耗时也是挺久的，大概在500ms上下。分析一下的话，比较耗时的部分应该是两个下标的确定部分了。首先for i in nums本身是个O(n)的循环，然后循环体中的index方法其实又是一个O(n)的操作，使得整体是一个O(n^2)的操作。
那么有没有什么办法，比如对于取下标不用index这种O(n)的方法？以空间换时间，自然可以开辟另一个结构去提前维护好整个列表中的下标情况，到时候直接去那个结构里取值就好了。比如用一个字典（哈希表）来维护：
def twoSum(nums, target): count = 0 idx_map = {} while count < len(nums): idx_map[nums[count]] = count count += 1 count = 0 while count < len(nums): m = target - nums[count] if m in idx_map and idx_map[m] != count: return [count,idx_map[m]] count += 1
虽然是两个循环，但是没有嵌套关系，所以总体还是O(n)，第一个循环将列表的值和下标分别作为键和值充入字典。不用担心相同的值会产生覆盖的情况，因为题目只说有一个解并给出这个解就好了，而且后面的循环遍历也是从前往后进行的，所以不会发生信息丢失，找不到配对的情况。 第二个循环中的idx_map[m] != count条件其实就是排除了同一个数使用两次的情况，如[3,2,5]和6，不能返回[0,0]
■ AddTwoNumbers
问题： 输入是两个链表节点实例，Python的话给出的链表定义是:
# Definition for singly-linked list. # class ListNode(object): # def __init__(self, x): # self.val = x # self.next = None
然后链表的val都是一个非负的int，可将它反向连接成一个数字，比如(3 -> 4 -> 2)这样一个链表的话，得到的是243这个数字。题目的输入就是这样两个链表，然后求两个链表得到的数字相加之后的和，再把这个和给转换成这个链表格式，要求输出是这个链表的头一个元素。
下面是我写的两种解法，耗时都在70ms左右。
解法一：
充分利用Python内置的各种类型转换和反序等方法，简单地将输入链表转化为list，处理为整数相加后再将得到的结果处理回一个链表。
def addTwoNumbers(self, l1, l2): """ :type l1: ListNode :type l2: ListNode :rtype: ListNode """ lst1,lst2 = [l1.val],[l2.val] while l1.next: l1 = l1.next lst1.append(l1.val) while l2.next: l2 = l2.next lst2.append(l2.val) tmp = list(str(int(''.join([str(i) for i in reversed(lst1)])) + int(''.join([str(i) for i in reversed(lst2)])))) last = ListNode(tmp[0]) for num in tmp[1:]: ln = ListNode(num) ln.next = last last = ln return last
解法二：
从前向后分别遍历两个列表，按照一般数学中相加，从个位数开始相加，超过10的则取余数进位，然后加下一位。不过考虑到两个链表长度不同，相加结果如果刚好要多进一个1等等情况，细节上的控制还是挺复杂的：
def addTwoNumbers(l1, l2): """ :type l1: ListNode :type l2: ListNode :rtype: ListNode """ res = dummy = ListNode(-1) stepUpFlag = False while l1 or l2: v1 = l1.val if l1 is not None else 0 v2 = l2.val if l2 is not None else 0 s = v1 + v2 if stepUpFlag: s += 1 stepUpFlag = False if s >= 10: s %= 10 stepUpFlag = True dummy.val = s if l1: l1 = l1.next if l2: l2 = l2.next if l1 or l2: newNode = ListNode(-1) dummy.next = newNode dummy = newNode elif stepUpFlag: newNode = ListNode(1) dummy.next = newNode break return res
■ Longest Substring Without Duplicate Character
问题： 寻找一个字符串中最长的无重复字符的子串长度。输入是一个字符串，输出只要求这个最长子串的长度即可。需要注意是子串而不是子序列，所以选出来的子串在原串中必须是挨在一起的。这个问题看似简单，我最开始也觉得肯定在笔记中哪里提到过做法。但是仔细找了找还真没找到…只好从头开始想。
想法： 要是放在以前，只是实现功能就好，那么我肯定会走上暴力的路… 暴力嘛，很简单，挨个遍历子字符串，碰到有重复字符的就跳过，然后找出最大长度的就好了。细节上也有很多可以优化的地方。因为没尝试就不写了。除了从字符串本身出发的暴力，也可以从符合要求子串出发。比如构建一个窗口，从len(s)长度开始分别去套各个相应长度的子串，判断是否有duplicate。当然两者其实本质一样，只是呈现方法不同。
然后想有没有更加聪明的方法来解决这个问题。假如我手上有一个字符串"abcacabcb"，首先我会从头开始数，abc三个没问题，到第四个a的时候发现重复，那只能把第一个a砍掉。继续往后，到第五个c，发现最前面的bc两个都要砍掉。这时就发现一些东西了。
从头开始遍历，当碰到一个字符前面出现过时，那么（大概）前面出现的那个位置之前的所有东西都不能要了。这种想法还需要考虑一下出现...a...b...b...a...这种情况的时候，此时扫描到最后一个a时，最前面的a前面的东西当然要砍掉，然而其实在这之前，扫描到第二个b的时候，就连同b前面的东西早就被砍掉了。所以此时应该关注的子串是从第一个b开始到a的这部分而不是两个a之间的那部分了。
每获得到一个合法的子串就把这个子串的长度记录下来，然后一路max到底就能得出最大长度了。另外回忆一下SumTwo，在遍历列表的过程中若要对列表做一个局部处理的时候，搞一个子列表再遍历会增加复杂度。一个比较好的办法是用哈希表（字典）来记录列表中元素和下标的映射关系。这里也是这么做的。
解法:
def lengthOfLongestSubstring(s): """ :type s: str :rtype: int """ charMap = {} maxLength = 0 stPoint = -1 # 这个变量记录的就是“要砍掉字符x之前的所有东西”，x所在的位置 # 初始化为-1是因为，抽取子串时，其实x也是不需要的。而在遍历的一开始，显然第一个字符是要算进来的，所以初始化不为0为-1 for i,char in enumerate(s): if char not in charMap: # 这个字符第一次首次出现在字符串中 charMap[char] = i maxLength = max(maxLength,i-stPoint) # 本字符到stPoint为止的内容是一个符合要求的子串，将其和当前maxLen中大者保存 else: if charMap[char] > stPoint: # 即...a...b...a...b...情况，此时要砍掉第一个b以前的所有东西，并且比价当前maxLen和两个b之间的长度大小，取其大者 maxLength = max(maxLength,i-charMap[char]) stPoint = charMap[char] else: # 即...b...a...a...b...情况，此时比较maxLen和第一个a到第二个b之间的内容长度，取其大者 # 注意，不能直接取i - stPoint因为maxLen不一定是两个a之间的长度。可能前面有更长的。 maxLength = max(maxLength,i-stPoint) # 更新本字符最后出现位置，为后面可能再次出现时提供stPoint参考 charMap[char] = i return maxLength
■ Median of Two Sorted Arrays
问题： 给出了两个各自已经按照从小到大排序的数组。求这两个数组构成的集合的中位数是多少。另外原题还要求总耗时应低于O(log(m+n))，m和n是两个数组的长度。
注意点： 如果利用Python编写，那么很朴素的思路就是将两个数组合并，然后排序新数组，然后找出中位数就行了… 如果不利用sort之类方法，全部自己写，则需要注意下逻辑的构成。
def median(nums1,nums2): nums1.extend(nums2) nums1.sort() leng = len(nums1) if leng % 2 == 0: return (nums1[leng/2-1] + nums1[leng/2])/2 else: return nums1[leng//2]
不利用 python捷径的办法：就是一个很普通的没有任何trick的算法。以扫描过中位数位置为目标(两数组长度之和是奇数还是偶数虽然会影响中位数的具体计算方式，但是在扫描右边界的选择上是一样的。奇数则扫描到下标为len//2的元素，而偶数也需要扫描到len//2来求中位数)，从头开始扫描两个数组，并且维护两个辅助变量num1和num2。扫描过程中逐渐从两数组剩余未被扫描的数字中选出最小者，然后始终保持num1小于num2。当扫描结束之后，num1和num2应该是这样两个数：假如将两个数组合并并安小到大排序得到数组N，总的长度是L的话，那么num1和num2应该分别是N[L//2-1]和N[L//2]。此时再根据L的奇偶不同，写出中位数即可。奇数的话直接取N[L//2]，偶数的话取N[L//2-1]和N[L//2]的平均。
可能需要注意的点： 边界处理，当两个数组为空的情况怎么办。另外还有一个很常见的情况是加入一个数组比另一个短很多怎么办？由于最开始扫描是在两个数组开头差不多同步推进的（只要两数组的值别差太大），那么必然会碰到第一个数组已经遍历到底，第二个数组还没遍历完，也还没有遍历到中位数位置。此时就需要根据遍历游标i1和i2与各自数组长度m和n之间大小比较的一个判断。
def findMedianSortedArrays(nums1, nums2): """ :type nums1: List[int] :type nums2: List[int] :rtype: float """ num1,num2 = 0,0 m,n = len(nums1),len(nums2) i1,i2 = 0,0 midLen = (m+n)//2 # midLen是为找到中位数需要遍历的两个数组中的元素个数（下标），比如若总长5，则需要遍历到总下标为2的，若总长8则遍历到4（中位数是3和4的平均，因此要到4） for i in range(midLen+1): # 因为midLen是下标，为了可以确定遍历到下标是midLen的，所以要+1 num1 = num2 # 始终确保num1是小于num2的 if i1 < m and i2 < n: if nums1[i1] <= nums2[i2]: num2 = nums1[i1] i1 += 1 else: num2 = nums2[i2] i2 += 1 elif i1 < m: num2 = nums1[i1] i1 += 1 elif i2 < n: num2 = nums2[i2] i2 += 1 else: return None if (m+n) % 2 == 0: return (num1+num2)/2.0 else: return float(num2)
■ Find longest palindromic string
问题： 寻找一个字符串中的最长回文子字符串。
可以暴力解，但是通不过time limit验证。另外可以通过DP 或者 manacher算法 来解开。
manacher解法： https://www.cnblogs.com/franknihao/p/9342907.html
■ zigzag conversation
问题： 函数给出一个字符串和一个rowNum参数N（一个整数），然后将字符串按照顺序从上垂直向下写N个。当写到S[N-1]字符时S[N]字符将写在右边一列的上面一行，S[N+1]写到S[N]的右上方，如此直到写回第一行，之后再垂直向下写。最终需要输出的是整个写出来的东西从左上角开始一行一行向右扫描获得的字符串。
例子：
"ABCDEFGHIJKLMN"，如果指定rowNum是3的话那么写成：
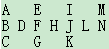这个图样的输出就是AEIMDBFHJLNCGK
如果rowNum是5，那么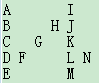
，所以输出就是AIBHJCGKDFLNEM。
解法：最直观的的，可以构建一个多维数组然后将上面所说的规则进行填写字符。当然这样做的空间开销可能比较大一些。如果仔细分析一下这个ZigZag的结构的话可以看到，其实每个字符和其下标的位置还是一定关系的。比如第k行从左到右的各个字符的下标应该依次是 (2*0+k)(2*n-k)(2*n+k)(4*n-k)...其中n等于rowNum-1 。按照这种规则，在做一些边界处理（比如第0行和第n行有可能会出现2n-k == 2n+k的情况，此时不处理边际问题可能会出现重复字符的情况），就写成了下面这段代码：
class Solution(object): def convert(self, s, numRows): """ :type s: str :type numRows: int :rtype: str """ n = numRows - 1 if len(s)-1 <= n or n == 0: # 边际情况处理 return s elif n == -1: return '' res = '' for k in range(n+1):# 遍历每一行 d = 0 res += s[d+k] # 加第一列的值 d += 2*n if k in (0,n): # 当k等于0或者n的时候，会发生类似于2n-k==n+k或者2n-k==2n+k，有些字符被算两次，所以特殊处理 while d+k < len(s): res += s[d+k] d += 2*n continue while d-k < len(s): # 一直以2n为步长不断向右，每向右一次都要尝试把d-k和d+k两个字符按照顺序打出来，如果碰到越界的情况表明本行打完，去下一行 res += s[d-k] if d+k < len(s): res += s[d+k] d += 2*n return res
■ string to interger
问题： 将一个字符串转化成整数。条件如下：
1. 字符串开头可能有若干个空格（真空格，\t\n这些不算）
2. 字符串可能不仅仅由数字组成，认为只有最开始的有效字符是数字的才能成功转换，比如100 words可以转化为100，但是words 100认为不能转化。不能转化的统统返回0
3. 数字的界限是[-2^31,2^31-1]，对于超出这个界限的数字，大于上限者返回上限，小于下限者返回下限。
解法： 利用Python的re模块可以偷个懒：
import re class Solution(object): def myAtoi(self, str): """ :type str: str :rtype: int """ m = re.match('^ *([\+\-]?\d+).*$',str) if not m: return 0 num = int(m.group(1)) if num > 2**31-1: return 2**31-1 elif num < -2**31: return -2**31 else: return num
■ regular expression matching
问题： 构造一个简单的正则表达式引擎。正规的正则表达式包括了很多种元素，这里的简单正则只指.和*两个pattern（.是通配符，*是前面字符的0到任意多个）。
这个题看似简单，实则猛如虎… 搞了半天没搞定，直接抄答案了：
class Solution(object): def isMatch(self, s, p): """ :type s: str :type p: str :rtype: bool """ m,n = len(s),len(p) if not p: return not s firstMatch = m >= 1 and (s[0]==p[0] or p[0]=='.') if n >= 2 and p[1] == '*': return self.isMatch(s,p[2:]) or (firstMatch and self.isMatch(s[1:],p)) else: return firstMatch and self.isMatch(s[1:],p[1:])
这个算法的想法核心是，比较原串和模式串的第一个字符是否匹配，记录下匹配结果firstMatch(当然，能匹配的前提是此时原串和模式串都不为空)，然后再看模式串的后一个字符，按照是否是*划分两种情况。
当是*的时候，意味着两种可能，1. N*(N是模式串的第一个字符)匹配空串，即*的含义是0个N字符，此时firstMatch肯定是False，此时可以直接跳过模式串的前两个字符，直接开始后面的匹配，因此递归调用了isMatch(s,p[2:])； 2. N*匹配到了一些N字符，此时需要有firstMatch是True，然后s往后一格而p保持不变，继续往后看s后面的字符是否还能和这个N*进行匹配。
当不是*的时候比较好办，只要看第一个字符匹配结果是否为True，如果是True就意味着可以将原串和模式串都向右移动一格继续匹配，如果是False，那么就意味着在第一个字符这里就不匹配也就没有了匹配后文的必要，直接返回False即可。
这种递归的办法虽然可以解出答案，但是并不是效率很高，更好的办法是使用DP。由于还不是很熟悉DP，就不写了…
■ Container with largest volumn
问题： 参数是一个数组，如果按照下标为横坐标，元素的值作为纵坐标那么我们可以画出一幅柱状图。现要以这个柱状图中的其中两个柱子作为边界，两者横坐标的差作为宽，两者值中较小的值为高，相乘得到的面积中最大时能有多少。
这道题很有意思，原题中应用色彩更强，说的是两个柱子之间其实是个木桶，问木桶最多可以装多少水。当然装多少水是由短的一端决定的。
解法：
暴力解肯定可以，找出每种柱子组合的面积然后找到最大的就行了。
然后在这个基础之上，我又想了一个优化。比如每遍历一个新的i的时候，都设置一个游标j从最后一个元素开始往前遍历数组h。当遍历到一个值比之前获得到的最大的h[j]小，那么这个就可以直接跳过了。因为宽不及之前的大，高也肯定不及之前的大。
然后按照这种想法去submit，没想到time exceeded了… 于是只能再想想。
仔细一想，其实对于一个固定的i来说，如果h[j-1]比h[j]小，那么无论如何都不可能将j-1后获得一个更大的面积。相反，如果h[j-1]比h[j]大，那么在宽上损失的一点面积是有可能通过高的提升补回来，从而比现有值大的。但是这样的补有另外一个隐含条件，那就是h[i]>h[j]。如果目前h[i]已经比h[j]要小了，那么j再减一，即使h[j]高到天花板，由于最终面积由短板决定，因此还是这么点。。
综合来看，只要h[i]>h[j]那么就可以将j -= 1尝试看是否有更大的面积。反过来，如果h[i]<h[j]，此时比j小的都不用试了，因为短板的i决定了最终面积，j继续减小，面积就算有变化也是往小了变。
再综合一下，一个很简洁的算法就是这样了： 让i，j两个游标分别从前后开始遍历，比较h[i]和h[j]，如果前者较小，那么i++，如果后者较小那么j--，两边向中间逼近，取整个过程中面积出现过的最大值就OK了。算法十分简单，但不太直观… 一下子想到有点难，总之先积累起来吧。
代码：
class Solution(object):
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
i,j = 0,len(height)-1
amax = 0
while i < j:
amax = max(amax,(j-i)*min(height[i],height[j]))
if height[i] < height[j]:
i += 1
else:
j -= 1
return amax
■ threeSum
twoSum的升级版，问题：
找出一个数组中满足所有a + b + c = 0的(a,b,c)。a,b,c之间无顺序要求。相同的一组abc在解集中只能有一个元素。
如 [-1, 0, 1, 2, -1, -4]的返回应该是[ [-1, 0, 1], [-1, -1, 2] ]
解决方案：
凭我能力还是没想出非暴力的算法… 所以还是抄了别人的解决方案。
首先，条件a+b+c=0是可以转化成-a = b+c。也就是说，可以选定一个a，取其相反数-a，然后再从剩余的数中找到一对b和c相加等于-a即可。这相当于是将3sum转化为一个2sum问题。但是这里还有两个问题，1是需要找出所有的解而非一个解，二是对于一个凌乱的数组而言，要找出这样一对数必然是要O(n^2)时间的。
所以第一步我们对输入的数组进行排序，在有序的时候可以通过首位两游标不断向中间逼近的办法来特定两个符合一定条件的元素。这样的过程是O(n)的，而不是两个for i,for j的循环嵌套的O(n^2)操作。然后从前到后去遍历各个元素，每遍历到一个特定的元素的时候将其视为a，然后在a后面的所有元素中找出b,c。由于a后面至少要有两个元素，所以这个遍历在倒数第三个元素处停止。由于b,c存在于一个有序的排列中，所以可以按照上面说的那样，头尾两游标去做。
这里还有一些可以优化的地方。比如遍历取a的时候，如果a已经大于0，那么此时b,c无论如何取b+c都>0，不会等于-a。另外，在遍历a以及两游标遍历的过程中，如果碰到几个连着相同的值，由于最终结果中相同的组合只能有一个，所以可以直接跳过。
因此最终写出的程序是这样的：
class Solution(object): def threeSum(self, nums): """ :type nums: List[int] :rtype: List[List[int]] """ nums.sort() fix = 0 res = [] while fix < len(nums) - 2: if nums[fix] > 0: break target = - nums[fix] i,j = fix + 1, len(nums) - 1 while i < j: if nums[i] + nums[j] == target: res.append([nums[fix],nums[i],nums[j]]) while i < j and nums[i] == nums[i+1]: i += 1 while i < j and nums[j] == nums[j-1]: j -= 1 i += 1 j -= 1 elif nums[i] + nums[j] < target: i += 1 elif nums[i] + nums[j] > target: j -= 1 while nums[fix] == nums[fix+1] and fix < len(nums) - 2: fix += 1 fix += 1 return res
■ GenerateParentheses
问题， 给出一个数字n，要求写出所有形式正确，并且包含了n对小括号"()"的字符串。比如当n=2时，应该返回的是["()()", "(())"]，由于")(()"这样的是非法的，所以不需给出。
算法：这个问题看起来似乎很水，但是卧槽…我想到的办法是暴力枚举，然后将每个字符串进行很早以前接触过的+1, -1那种形式的is_valid检查。不过暴力果然太low了，下面这个算法是基于DFS的生成：
def generate(n): res = [] def backtrace(s, left, right): ''' 递归过程中s保持为一个合法的字符串 left，right分别表示该字符串中左、右括号的个数 ''' if len(s) == 2*n: res.append(s) return if left < n: backtrace(s+'(', left+1, right) if right < left: backtrace(s+')', left, right+1) backtrace('',0,0) return res
■ DivideTwoNumber
问题： 给出dividend（被除数）和divisor（除数），做一个整数除法并返回结果。要求不要用到乘号除号或者取模操作。另外还有一个限制默认int表示范围是[-2^31, 2^31-1]，超出此范围的结果返回封顶值即可。
算法： 这个题看起来就非常有意思。一开始我想不用乘除法，大不了不断减去除数，看减去了几次就行了。然而对于除数很小的情况，很容易TLE。这说明线性地一个一个减去除数太慢了，于是想到能否加快这个减小的过程。如果可以用乘号，那么可以直接另divisor *= 2，这样可以两倍两倍地减除数，系数可以调得很大。可是不让用乘号啊怎么办…
反正我自己没想到… 后来看了下别人的答案，发现有位操作这条路可以走。（受到启发，以后可用位操作来代替*2）
为了方便令被除数是a，除数是b，那么通过不断的b << 1可以将b扩大到 b * 2 ^ n，当n再加上1则b会大于a。这样一次减小就可以将a的“一大半”都减掉，比较有效率。对于a减小之后剩余部分，可以重置n后做一个同样的操作。这样a减小的速度是指数级的，比原先线性的要快很多。
其他无非就是一些正负的考虑，以及溢出的处理等等，解释和心得都写在注释里面了：
def divideTwoNumber(,b):class Solution(object): def divide(self, dividend, divisor): """ :type dividend: int :type divisor: int :rtype: int """ minus = (dividend < 0) ^ (divisor < 0) # 异或操作判异号，这个比较有意思，一般只想到a<0 == b<0之类的 a,b = abs(dividend),abs(divisor) # 撇开同异号影响后只关注绝对值 res = 0 while a >= b: c = -1 powb = b while a >= powb: # 寻找a能承受的最大c powb <<= 1 c += 1 a -= b << c # 减去a的“大半部分” res += 1 << c # 记录下这个大半部分其实包含了几个b return max(-res,-2**31) if minus else min(res,2**31-1)
顺便一提，看了其他还有答案是用math.exp结合math.log，相当于是把普通运算做成了指对运算。也有用// 或者 *=这类擦边球的。。不过包括上面的位运算在内，本质上要计算出这个商总归是要进行乘除运算的，只不过是如何在代码里不提到乘除号。可以说这个题也算是个让你熟悉语言各种非简单四则运算套路的题目。
■ Find First and Last Position in Sorted Array
问题： 输入是一个数组和一个target值。这个数组array是经过排序的。要求返回这个数组中，target元素第一次出现和最后一次出现的下标值。如果target元素根本不存在于数组中则可以返回[-1,-1]。
比如[5,7,7,8,8,8,10]，8这样一组输入，得到的输出是[3,5]。另要求算法的时间复杂度是O(logn)
解决： 看到O(logn)，想到了可以通过二分查找来解决。于是第一个比较朴素的想法是通过二分查找定位到某个target元素后，以此为中心，向两边扩散寻找最左边下标和最右边下标。不过如果target元素重复次数比较多，这样扩散操作会导致O(n)的复杂度，因此不算是一个很好的办法。
另一个办法是通过两个二分查找分别找到最左和最右target的下标。我们知道一般的二分查找，默认扫描数组中不存在重复元素，这也就是说如果存在多个target的时候，mid碰到某一个就立即返回。 为了找到最左或者最右的target，势必要将二分查找主循环中的那个return语句去掉。
一般的二分查找：
def search(nums,target): low,high = 0,len(nums) - 1 while low < high: mid = (low + high) // 2 if nums[mid] == target: return mid if nums[mid] < target: low = mid + 1 else: high = mid - 1 return -1
然后我们再来分析下，如果将return语句去掉了，那么nums[mid]值仍然小于target的时候无所谓，大于等于target的时候都会走else分支。而等于target的时候high的继续左移则可以保证high有可能可以移动到最左侧的target元素的下标。不过需要额外注意的一点是，如果mid的位置刚好是最左边的target，那如果让high = mid - 1，此时[low,high]区间内就不存在target元素了，最终会返回-1。 这显然不是我们期望的，因此需要考虑如何修改。 其实只要将high = mid即可。这样可以保证high的左移不会超出target的范围。
当然，跳出循环时，如果nums[high]的值不是target，这就说明原数组中没有target元素，可以直接返回-1了。
另一方面，上面的修改是针对求最靠左的，如果是求最靠右的呢？只要修改两个地方就可以了，就是把nums[mid] < target改为nums[mid] <= target ； 以及把high = mid改回high = mid - 1。由于有了等于号，相当于low最大可以到target带的最右端，也就是我们想要求的东西了.
不过这里还有一些细节需要注意，因为在这样的代码中，low可以右移且high可以左移，如果刚好low遍历到target带最右端，且high刚好是low+1，此时mid是low，而nums[mid]满足<=target，所以low会再+1，此时low和high相等，跳出循环。所以说，要找到target带最右端的值，在跳出循环之后还需要看下nums[low]是否是target，如果是那么可以直接返回，如果不是，就得返回low - 1
综上，代码：
class Solution(object): def searchRange(self, nums, target): """ :type nums: List[int] :type target: int :rtype: List[int] """ if len(nums) == 0: return [-1,-1] # 空特殊值处理 low,high = 0,len(nums)-1 left,right = None,None while low < high: # 第一个循环确定target带左端值 mid = (low + high) // 2 if nums[mid] < target: low = mid + 1 else: high = mid if nums[high] != target: return [-1,-1] left = high low,high = 0,len(nums) - 1 while low < high: # 第二个循环确定target带右端值，相比第一个循环代码上两处改动 mid = (low + high) // 2 if nums[mid] <= target: #修改处1 low = mid + 1 else: high = mid - 1 # 修改处2 if nums[low] != target: # low有刚好出target带的风险，做一个额外判断 right = low - 1 else: right = low return [left,right]
值得一提的是，上下两个循环也是解题中经常会用到的两种二分查找模式。上者是“查找第一个不小于目标值的数” 或者 “查找最后一个小于目标值的数” 的模式（这两个问题之间的相关性是，前一个问题的解的下标减1就是后一个问题的解的下标），下者是“查找最后一个不大于目标值的数” 或者 “查找第一个大于目标值的数”，两个问题相关性类似。
