【数据结构】 二叉树
【二叉树】
二叉树是最为简单的一种树形结构。所谓树形结构，其特征（部分名词的定义就不明确给出了，毕竟不是学术文章。。）在于：
1. 如果是非空的树形结构，那么拥有一个唯一的起始节点称之为root（根节点）
2. 除了根节点外，其他节点都有且仅有一个“父节点”；除此外这些节点还都可以有0到若干个“子节点”
3. 树中的所有节点都必须可以通过根节点经过若干次后继操作到达
4. 节点之间不会形成循环关系，即任意一个节点都不可能从自身出发，经过不重复的径路再回到自身。说明了树形结构内部蕴含着一种“序”，但是不是线性表那样的“全序”
5. 从树中的任意两个节点出发获取到的两个任意子树，要不两者无交集，要不其中一者是另一者的子集
限定到二叉树，二叉树就是任意一个节点至多只能有两个子节点的树形结构。也就是说，某个节点的子节点数可以是0,1或2。 由于可以有两个子节点，所以区别两个子节点可以将其分别定义为左子节点和右子节点。但是需要注意的是，若一个节点只有一个子节点，那么也必须明确这个子节点是左子节点还是右子节点。不存在“中子节点”或者“单子节点”这种表述。
由于上述规则对所有节点都生效，所以二叉树也是一个递归的结构。事实上，递归就是二叉树一个非常重要的特点，后面还会提到很多通过递归的思想来建立的例子。
对于左子节点作为根节点的那颗二叉树被称为相对本节点的左子树，右子树是同理。
■ 基本概念
空树 不包含任何节点的二叉树，连根节点也没有
单点树 只包含一个根节点的二叉树是单点树
至于兄弟关系，父子关系，长辈后辈关系是一言既明的就不说了。
树中没有子节点的节点被称为树叶（节点），其余的则是分支节点。一个节点的子节点个数被称为“度数”。正如上所说，二叉树任意节点的度数取值可能是0，1或2。
节点与节点之间存在关联关系，这种关联关系的基本长度是1。通过一个节点经过若干个关联关系到达另一个节点，经过的这些关联关系合起来被称为一个路径。路径的长度等于关联关系的个数。为了统一，通常把一个节点到其自身的路径长度为0。
二叉树是一种层级结构，某个节点所在的层数是根节点到达此节点路径的长度。因此根节点所在第0层。所在第k层的节点，子节点在第k+1层。
一棵树可以取到的最大的路径长度称为树的高度or深度。单点树的高度为0。
■ 基本性质
下面列出一些二叉树的基本性质，证明就不给了，能力有限…
非空二叉树的第i层最多可以有2^i个节点。高度为h的二叉树最多可以有2^(h+1) - 1个节点。
对于任何非空二叉树，若其叶节点个数为m，度数为2的节点个数为n。那么m = n + 1。虽然懒得抄证明了，但是可以感觉到，加上去的这个1，如果算在根节点上是比较合理的。
● 满二叉树和扩充二叉树
所有分支节点的度数都是2的二叉树是满二叉树。需要强调是分支节点。即最终叶节点并非一定要完全是2^n个那么完整的那种。
对于一个二叉树T，添加上所有有必要的叶节点，使得T中的所有节点（包括分支和叶节点）的度数都变成2，从而T变成一个满二叉树。得到的这个满二叉树相对原树T而言就是一个T的扩充二叉树。被新添加上去的这些叶节点被称为外部节点，新扩充二叉树中的所有分支节点（包含原树的分支节点和叶节点）被称为内部节点。根据上述基本性质的第三条，可知外部节点个数m = 内部结点个数n + 1。
● 完全二叉树
对于高度为h的二叉树T，若0到h-1层所有层都符合，i层的节点个数是2^i个；且第h层节点数小于2^h个时，所有h-1层度数为1的节点的子节点都是左子节点的话，那么就称T为完全二叉树。需要注意区别完全二叉树和满二叉树之间的区别。比如下面这个就是一个完全二叉树但不是满二叉树。
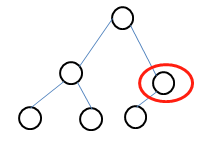
第0层有1个，第1层有2个节点，是完全二叉树。但是红圈中的节点度数是1，不符合满二叉树要求。
对于总含有n个节点的完全二叉树，其高度h是log2n向下取整。由于完全二叉树在0到h-1层为止的完整性，有一些很好的性质。比如从根节点开始，把根节点标号为0，之后按从上到下，从左到右依次给树中的所有节点编号，那么可以看到对于编号为i的节点，
1. 其父节点的编号是(i-1)/2，这是int除法，自动向下取整
2. 若2 * i + 1 < n则其左子节点的序号是2 * i + 1，否则没有左子节点
3. 若 2 * i + 2 < n则其右子节点的序号是2 * i + 2，否则没有右子节点
也是因为其完整性，可以将一个完整二叉树比较好地投影成一个连续表。如按照上面描述的规则那样对树节点进行编号的话，那么在表中仅凭下标就可以轻松得查找到某个特定节点在树中的父子节点。
从直观的图上来说，完整二叉树是很丰满的图形。一个二叉树越是丰满完整（实际上就是指其分支节点中度数为1的节点占比比较低），其树的最长路径越接近O(log n)的。相反越是单薄的，最长路径接近O(n)的。极端的情况，当所有的节点都只有一个子节点，那么二叉树其实就变成了一个连续表了。
■ 二叉树的抽象数据类型
如果构造一个二叉树类，可能会需要下面这些方法和属性：
class BinTree: BinTree(data,left,right) # 构造二叉树 is_empty() # 判断是否是空二叉树 num_nodes() # 返回总节点数 data() # 获取根节点数据 left() # 获取左子树 right() # 获取右子树 setLeft(binTree) # 设置左子树为指定树对象 setRight(binTree) # 设置右子树为指定树对象 traversal() # 遍历树用的方法，比如python实现就可以让它返回一个迭代器
作为一个数据结构，二叉树的本职工作是存储数据。树的节点就是拿来存储数据用的。因为根节点在一个树里处于比较特殊的地位，所以一般用树的根节点作为特征来指定一颗树。根节点作为获取二叉树中数据的入口而存在。除了根节点，组成一棵树的另外两部分就是左子树和右子树。这三者组合起来就可以完整地描述一棵树了，这也是为什么构造方法中采用了这三个参数，并且类中给出了这三个属性各自的get和set方法。
除去这些方法外，最关键的方法就是如何遍历二叉树了。
由于二叉树是个二维结构，遍历时到达一个节点之后我们可能有两个前进方向，因此遍历二叉树分成两种模式，分别是深度优先和广度优先。
● 深度优先遍历
深度优先表示，从根节点出发遍历时优先向一个叶节点方向遍历，不撞南墙不回头。
上面说过了一个二叉树有三个要素即根节点，左右子树。在遍历到一个特定的位置时，这三个要素先后如何处理是个问题。首先需要说明，左子树和右子树可以经过树中心线的镜面对称从而互换，因此暂规定左子树总是先于右子树处理。另左右子树分别为L,R，根节点为D的话。那么遍历顺序有下面三种可以选择：
DLR 被称为先根序
LDR 称为中根序，也称为对称序
LRD 称为后根序
选定任意一种顺序，从根节点开始判断，当L或者R存在时则转入相关子树判断，否则进行顺序规定的下一个对象。只要整个遍历过程选定了一个顺序不变化，那么最终就可以一个不多也不少地遍历完树的所有节点。
针对下面这个二叉树实例，根据不同的遍历顺序可以得到三个不同的节点序列：
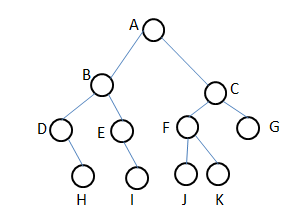
按照DLR顺序得到的是 A B D H E I C F J K G 序列。这个序列对这个二叉树来说也被称为是先根序列
按照LDR顺序得到的是 D H B E I A J F K C G 序列。这个被称为对称序列。
按照LRD顺序得到的是 H D E I B J K F G C A 序列。这个被称为后根序列。在尝试写出序列的过程中就可以感受到，其实二叉树的遍历是具有很强的递归色彩思想的。二叉树本身就可以视为将两个自身类对象作为属性的类实例。因此递归在所难免。
同样的一棵树，我们可以根据遍历顺序的不同而写出多种不同的序列。所以得到一个序列之后并不能还原出树来。事实上，告诉一个序列并且告诉这个序列的遍历顺序，也无法还原树。但是可以证明，如果知道了一棵树的对称序列，且知道另一个序列的话，是可以唯一确定一个二叉树的。
● 宽度优先遍历
宽度优先遍历时，由于来到一个子树之后不急着马上处理这个子树而是回头看还有哪些平级的子树。所以宽度优先的遍历不能用递归来做。相对的，我们可以设计一个栈，把相关同级的子树都压入栈，确认已经没有同级的子树之后再从栈中取出各个子树来处理。
按照宽度优先的顺序遍历得到的序列是层次序列，比如上面给出的示例树，其层次序列是A B C D E F G H I J K，和我们习惯性的编号顺序一致。
很多时候，遍历的目的并不在于真的要遍历所有节点，而是为了搜索我们一个想要的节点。根据树的形状以及实际数据分布不同而采用的不同的遍历模式&遍历顺序，有可能会给最终搜索的效率带来很大的影响。（比如我们想要找上例中的J节点，采用两种模式的四种顺序，J每次出现的时间点都不同）选择一个最优的遍历顺序有时候是高效解决问题的关键。
■ Python的二叉树实现
创建节点类，再据此实现树类，虽然可行，但是有些繁琐。目前我们仅为了做一些简单的演示，所以借用一些现成的数据类型也可以实现简单的二叉树。比如一个多重嵌套的列表。规定一棵树是一个三元列表tree。tree[0]保存根节点的值，tree[1]和tree[2]分别是左子树和右子树，分别也都可能是三元列表。当没有某个子树的时候，就用None来代替。
于是我们就可以获得一个简单的树了：
['A', ['B', ['C',None,None], ['D',None,None] ], ['E',None, ['F',None,None] ] ]
叶节点是[xxx,None,None]，而分支节点后两个值中至少有一个不为None。这整个嵌套列表的维度 = 树的高度 + 1。
● 利用这个二叉树进行简单应用 —— 表达式二叉树
对于简单的数学表达式（用加减乘除，大于小于号等二元运算符以及相关数字量组成的表达式），由于每个运算符都是二元的，所以表达式其实是可以很好地对应到一颗二叉树的。而且这是一棵满二叉树。树中所有叶节点都是数字量，所有分支节点加上根节点是运算符。比如以这个算式为例：
( a - b ) * ( c / d + e ) 总共包含了5个数字量和4个二元运算符（这里姑且先不管括号的存在）。在这种情况下，可以将这个表达式转化成一个二叉树如下：
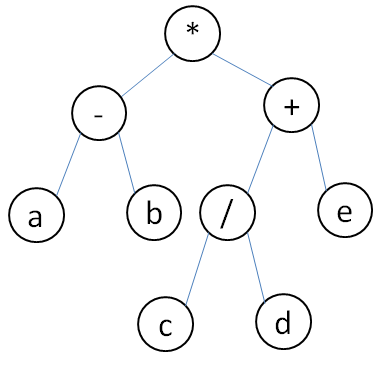
可以看到，二叉树由于其二维的层级结构，天然就带来了括号的作用，所以括号可以不在树中体现，就能构造出和算数表达式相对应的二叉树了。
然后再来看看如何遍历这棵树。首先我们只考虑深度优先模式，然后如果采用中根序遍历，得到的是a - b * c / d + e，基本上就是去掉括号的原表达式。但是也可以看到，由于遍历的过程将二维信息一维化，原本的一些计算顺序的信息丢失。所以中根序并不是好的遍历表达式二叉树的办法。
采用前根序得 * - a b + / c d e，采用后根序得到 a b - c d / e + * 。这两者分别是之前在学习栈的时候提到过的，算数表达式的前缀表达法和后缀表达法。根据之前的了解，两者无需括号，是自带了计算顺序信息的。
在得到一个表达式二叉树之后，我们当然可以得出其后根序列，然后根据之前说过的利用栈的方法来求表达式的值。另一方面，着眼于二叉树整体，采用递归的办法也是可行的。这里的递归思想大概是这样的: 到达一个树的根节点时，判断其两个分支是否都是叶节点了。如果不是，则递归进入该子树进行处理，如果都是叶节点（即数字量了），那么根据根节点给出的运算符做出相关运算，并将得到结果作为本树（或者说该根节点）的值保存下来，返回上层，直到计算出整个表达式树根节点的值。
用函数的语言来说可以是这样的：
假如我们的树是这样的
expTree = ['*', 3, [ '+', 2, 5 ] ]
这个表达式原型是3 * ( 2 + 5 )。为了表达的方便，所有叶节点没有写成[num,None,None]的形式。
def is_basic_exp(ins): return not isinstance(ins, list) def eval_exp(ins): if is_basic_exp(ins): return ins op, a, b = ins[0],eval_exp(ins),eval_exp(ins) if op == '+': return a + b elif op == '-': return a - b elif op == '*': return a * b elif op == '/': return a / b else: raise SyntaxError('Wrong choice of operator')
以上就是计算一个由List实现的表达式二叉树结构的值的函数，采用递归的办法。is_basic_exp是个辅助函数，当目前的“树”不是List类型，说明已经是叶节点（基于上面的那个简化操作，否则可以判断ins[1] == None and ins[2] == None）。此时就可以直接返回叶节点的值。如果当前不是叶节点，那么就去除本节点的操作符以及两个子节点的值。子节点有可能也不是叶节点，因此递归。如果两个子节点都是叶节点，那么刚好就获取到了两个值和一个操作符。接下来根据操作符进行相应的计算即可。
当然这个函数还是存在一些缺陷的。比如未对除数为0的情况作出判断，为验证传入参数的类型是不是都是数字类型等等。
■ 优先队列
优先队列是一种重要的缓存结构，基于对二叉树的认识可以高效地实现一个优先队列因此可以看做是一种对二叉树的应用。
● 基本概念
优先队列本质上也是一个线性表。和一般的队列或者栈不同的是，除了每个元素的值本身外，每个元素还有一个优先度的值。每次对优先队列进行访问或弹出操作时，都必定会获取到当前队列中优先值最高的元素。如果队列中有多个优先值一样的元素，那么可以根据队列内部自定义的规则给出结果。
● 简单实现
要用Python实现优先队列的话，可以选择List作为基本的容器。
另外，为了能够实现“获取时总是获取到优先度最高的那一个”这样一个目的，可考虑的实现方式可能有两种。第一，在创建与插入元素到队列的时候时刻保持队列根据优先度的顺序排列，这样在获取元素的时候只要在队尾获取即可；第二，根据简单的方法创建以及插入元素，在获取元素的时候再到队列中去寻找优先度最高的一项。综合对比两项来看，分别是把难度放在了插入和获取上。下面采用第一种方案实现
class PiorQueue: def __init__(self,elist=[]): self._elems = list(elist) self._elems.sort(reverse=True) def enqueue(self, e): i = len(self._elems) - 1 while i >= 0: if sellf._elem[i] <= e: i -= 1 else: break self._elems.insert(i+1,e) def peek(self): return self._elems[-1] def dequeue(self): if self.is_empty(): raise Exception('empty queue') return self._elems.pop()
这个类创建的时候接受了一个可迭代对象作为参数（这里使用了可变对象作为参数的默认值，这是不值得提倡的。因为方法/函数参数的默认值只随函数定义在内存中保存一次，之后每次调用该方法/函数时默认值都是引用到这个地址。使用可变对象有可能导致不同时间调用方法/函数的默认值不同。），并且按照从小到大排序。
enqueue是新增元素入队列的方法，可以看到我们默认将元素值作为其优先度的值，从队尾开始逐渐遍历，找到一个比新增元素值（或者说优先度）大的，然后把这个元素插入到这个元素位置前面。
peek和dequeue方法都很简单。不难看出，插入时方法的复杂度是O(n)而另两个都是O(1)的。
● 用树形结构实现
如果评价上述用线性表/连续表实现优先队列效率比较低的话，分析一下，主要的瓶颈就在于插入时要进行一个O(n)的遍历。如何将这个很“线性”的遍历变得更加高效称为关键、
正如前面说过，一个线性结构可以很好地映射到一个对应的完全二叉树结构中。自然，一个有序的线性表也可以。一个有序的线性表对应出来的完全二叉树结构被称为堆。堆的根节点是堆顶，从堆顶向叶节点方向呈现出来值上的顺序是堆序。堆序是从小到大，即堆顶的值是最小值的情况，成为小顶堆，反之为大顶堆。
如将一个承载着优先队列的线性表对应成一个堆，那么可以想象，由于堆本身的完全二叉树的性质，将原本一维的，从上到下依次遍历的方式改成了二维的方式。这使得遍历的效率大大提高。原本O(n)复杂度的操作将会变成O(logn)。类似的，通过堆来实现优先队列同样要解决插入和删除的问题。即如何在合适的位置插入一个新元素以及如何在删除一个元素之后调整原堆，保持它的堆序。
下面将更深地讲述堆和堆的性质，以及用堆实现优先队列的种种。
■ 堆
正如上面所说，堆比较重要的特点是它有特定的堆序。从定义上来说，堆对应的是一个完全二叉树，其最下层的叶子节点可以不满。同时由于堆序，其保证任意一个节点都小于or大于其两个子节点中的值。以小顶堆为例，从堆中任意选取一条路径，那么得到的就一定是从上至小依次递增的一条有序路径（暂时先不考虑不同路径之间的节点值的大小比较关系）。
堆还具有以下的性质：
1. 在堆的最后append一个元素，整个结构仍然保持是一个完全二叉树，但是并不一定是堆（新加入的元素不满足堆序）
2. 堆顶一定是整个堆中最小or最大的值。堆中的任意一个节点下的两个子树也都是堆。
3. 改变堆顶的值，整个堆保持完全二叉树结构，但是不一定是堆
4. 去除堆中最后一个元素，整个结构保持是一个堆
如果将堆作为优先队列的载体。那么显而易见有两个问题需要解决。第一，把一个新元素入堆的时候如何将其放到合适的位置；第二，从堆中取出最优先元素之后，剩余元素如何编排成一个堆。在下面的实现分析中我们可以看到，这两个操作都是O(log2n)的，相比于之前插入时要O(n)的操作，显然堆作为载体的效率更高
● 向上和向下筛选
下面以小顶堆为例讲述。
插入一个元素到堆，如何才能将它准确放入到合适的位置。其实这个解决办法很朴素，首先我们将元素append到堆末尾，此时由于堆序不一定得到保持，堆称为一个普通的完全二叉树。接下来就是找回堆序，最简单的办法就是将位于堆末尾的那个新元素依次向上和父元素比较。对于大于父元素的情况，则交换两者位置。对于小于的情况，则表示当前新元素已经处于合适的位置了。这一整个过程就叫向上筛选。其巧妙之处在于注目于单条路径，维护其堆序的正确性，对于其他的路径保持不变。
相对的，如果是从堆中弹出最优先（就是堆顶）元素，那么堆顶此时空了。我们可以从堆末尾弹出堆的最后一个元素M赋值给堆顶。类似的，堆序崩坏，需要找回堆序。此时就可以将M和两个子节点比较，选择其中最小的那个作为堆顶。如果此时M已经是三者中最小，就可以不用变了；否则交换最小者和M的位置。接下来就是继续关注M，进行递归的操作。这整个过程类似于上述过程的反过来，所以是向下筛选。
下面开始基于堆做一个简单的有限队列的实现：
class PriorQueue(): def __init__(self,elist): self._elems = list(elist) if elist: self.buildHeap() def is_empty(self): return not self._elems def peek(self): if self.is_empty(): raise ValueError('Queue is empty') return self._elems[0] def enqueue(self,elem): self._elems.append(elem) self.shiftup(elem,len(self._elems)-1) def dequeue(self): if self.is_empty(): raise ValueError('Queue is empty') elem0 = self._elems[0] lastElem = self._elems.pop() if not self.is_empty(): self.shiftdown(lastElem,0,len(self._elems)) return elem0
这个类和之前通过list实现的消息队列是类似的。不过目前这里还有三个方法，buildHeap，shiftup和shiftdown没有实现。第一个是用来构建堆的，后两者则分别是向上和向下筛选。下面首先看shiftup和shiftdown两个方法：
def shiftup(self,element,lastIndex): currentIndex,parentIndex = lastIndex,lastIndex//2 while currentIndex > 0: if self._elems[parentIndex] > element: self._elems[currentIndex] = self._elems[parentIndex] currentIndex = parentIndex else: self._elems[currentIndex] = element break def shiftdown(self,element,begin,end): currentIndex,child1,child2 = begin,begin*2+1,begin*2+2 while child2 <= end: minChild,minChildIndex = (self._elems[child1],child1) if self._elems[child1] < self._elems[child2]\ else (self._elems[child2],child2) if element > minChild: self._elems[currentIndex] = minChild currentIndex = minChildIndex child1,child2 = currentIndex*2+1,currentIndex*2+2 else: self._elems[currentIndex] = element
阅读代码之后其实可以发现，虽然在描述中说的是将父子节点进行互换，但是实际上没有进行x,y = y,x这样的操作。这也算是一个小优化点吧，实际上是先将要进行筛选的值“握在手中”，逐渐进行筛选，碰到需要调换的，比如向上筛选过程中碰到父节点比我手里的值大的情况，那么就将父节点那个值赋值给当前节点，再将当前节点标记为父节点，此时并不直接将父节点赋值为我手中的值，而是选择继续往上看，这样到头来我只需要直接把手中的值放到合适的位置，避免了很多不必要的赋值操作。
相比于向上筛选，向下筛选稍微复杂一些，主要是要做一些哪个子节点的元素更小之类的判断。此外两个方法都留出了begin,end之类的边界指定接口，这样不仅仅是筛选到堆顶/最下层的情况，任意层级指定的筛选都可以实现。
接下来让我们来考虑一下buildHeap方法如何实现。在这个类的构造方法中我们可以看到，其实是将外部传入的elist参数作为构造树的一个基石。顺便一提将self._elems = list(elist)可以避免可变对象参数默认值陷阱以及防止修改原对象等等。这个列表本身其实已经对应了一个完全二叉树结构了。假如其长度为end = len(self._elems)，那么从 end // 2 的那个下标（包括其自身）开始的所有节点都是叶子节点。（请注意，叶子节点不一定是最下层的，还有可能是倒数第二层的）
有两种方案可以选择。1. 我们另声明一个空堆，然后将列表中数字逐个append入堆，并进行向上筛选，最终形成堆。
2. 我们也可以基于现有堆直接作出调整。由于堆要求从堆中取出任意一个子树，都可以形成一个堆。对于那些叶子节点来说没问题，一个节点肯定是一个堆，而对于下标为end // 2 - 1的节点开始一直到整个堆的堆顶，有没有堆序却还是不一定的。所以我们要做的工作就是从下至上，从右至左按照下标递减顺序依次对各个尚未形成堆序的完全二叉树形成堆序，即进行向下筛选（不向上筛选是因为向上筛选走的往往是整个堆中的一条路而忽视了其他路的检查，而向下筛选由于筛选时会进行子节点大小的判断，算是兼顾了所有路线，因此可以保证最终整体堆序的形成）。基于这样的思想很快就可写出代码了：
def buildHeap(self): end = len(self._elems) for i in range(end//2, -1, -1): #range生成的是end//2到0的倒序列表 self.shiftdown(self._elems[i], i, end)
我们实现的shiftdown方法刚才一直用于弹出堆顶，可能会给我们造成一定思维定式的困扰。其实，shiftdown方法本身并没有做过任何减小self._elems的操作，也就是说它不包含“弹出”的操作。它做的，无非是接受外界的一个指标（element）和起始节点（begin）和结束节点（end），然后在起始节点和结束节点之间寻找一个合适的位置插入element这个值而已。所以构造堆方法中做的工作，是对每一个待调整的节点，取出其值，然后看将它放在它的子树中的什么地方最合适。合适的判断标准则是要求最终能形成一个堆。
另外可以计算得知，构造堆操作的复杂度是O(n)的。但是在整个堆的使用过程中这个操作只做一次，相比于每次插入都是O(n)的list实现而言是效率更高的。
● 堆排序
我们说的排序通常是指对一维数组的排序。堆的有序性是二维的，而如果将其转化为一个一维结构则不一定有序。不过利用堆在堆顶是最小（或最大）的性质，依次弹出堆中所有的元素，那么按照弹出的顺序就可以得到一个有序的线性列表了。
为了最大限度得到牛逼的算法，还可以考虑一下空间的使用。比如每次从堆中获取出堆顶后，由于接下来要把堆最下右的值给pop出来做向下筛选，所以堆最后会空出一个格子，正好可以用来放堆顶的这个值。此后再进行弹出，向下筛选的过程时只要不把最后一个已经保存了有效值的格子不算进去就行了。如此周而复始，最终可以不用一点外部空间就解决排序的问题。
下面是对于堆排序实现的一段代码（抄书的），感觉十分牛逼，将代码精简做的很好
def heap_sort(elems): def shiftdown(elems,e,begin,end): i,j = begin,begin*2+1 while j < end: if j+1<end and elems[j+1]<elems[j]: j += 1 if e<elems[j]: break elems[i] = elems[j] i, j = j, 2*j+1 elems[i] = e end = len(elems) for i in range(end//2,-1,-1): # 进行堆构建 shiftdown(elems,elems[i],i,end) for i in range(end-1,0,-1): tmp = elems[i] elems[i] = elems[0] shiftdown(elems,tmp,0,i) #只到i不到end，不影响已经完成排序部分
这个排序的复杂度是这样, 首先堆构建是O(n)的，后面进行排序的循环，循环体中是O(logn)而总共进行了n次，所以总的时间复杂度是O(nlogn)。由于基本没有使用额外的空间，空间复杂度是O(1)的。有关排序的更多方法，以后也会提到。
■ 基于优先队列进行离散事件模拟
这部分内容和二叉树没有什么关系，但是书上写在这里，而且觉得它的设计模式比较有趣，就简单记录一下。
首先要确认什么是离散事件。离散事件是指那些不定时发生的，且发生之后会影响到接下来事件的事件。比如书提到的，一个海关要检查车辆，有N条通道，每条通道在一个时间点上只检查一辆车。车是一辆一辆随机时间间隔地到海关门口接受海关检查。细节上，如果当前N条通道都有车接受检查，那么车在海关门口排队直到有通道空闲，每辆车接受检查的时间也不固定，因此有可能会出现某条通道相比于另一个通道先被占据而后被释放的情况。某辆车通过检查后离开，当前通道得到释放可以接受下辆车。
看了上述描述，如果要用一个计算机过程来模拟这个离散事件过程，我们最容易想到的就是线程池+队列模型。每个通道作为线程池中的一个工作线程，而外部的一个队列维护还在排队等待接受检查的车辆。简单明了且和场景切合度很高。
而书中提供了一种不用多线程来模拟的方案。其核心要义是将车辆到达&离开抽象为“事件类”Event，Event类带有属性c_time表示事件开始的时间，同时实现了__lt__和__le__方法，这样就可以利用优先队列模型将各个事件维护入队，而优先队列的优先度就是按照事件实际发生的开始时间，越早的越优先。外部的排队等待的车辆，用一个简单队列维护起来就行了。然后模拟过程中，模拟主对象不断地从优先队列中取出事件进行处理。由于事件按照发生时间排序了，所以可以存在后入队先执行的可能性。另外为了保证事件不中断地发生，可以考虑另外定义一个EventFactory之类的类或者在Arrive以及Leave事件的执行方法中直接生成下一个Arrive/Leave事件。
具体的代码就不写了，很长也很绕，就当做是一个思维练习吧。
■ 二叉树的类实现
前面Python中使用二叉树时默认载体往往是list或者tuple，还是一种比较抽象的概念，但是很好地体现出了二叉树和线性列表间的关系。接下来要说的是如何通过自定义二叉树类来实现一个二叉树。通过类实现的数显然可以更加直观，使用起来更加方便。
● 节点类
二叉树有很多节点构成，节点类是二叉树类的基础。如果将子节点作为属性加入到节点类中，那么很明显，二叉树类本身也是一个节点类。或者说，二叉树类和节点类是没有区别的。一个简答的节点类可以写成这样：
class BinTNode: def __init__(self,data,left=None,right=None): self.data = data self.left = left self.right = right
那么一个简单的二叉树就可以表示为BinTNode(1,BinTNode(2),BinTNode(3))。基于这种类结构，以及前面提到过的很多关于递归进行树遍历的思想，可以写出下面两个方法：
def countNodes(t): if t is None: return 0 return 1 + countNodes(t.left) + countNodes(t.right) def sumNodes(t): if t is None: return 0 return t.data+ sumNodes(t.left) + sumNodes(t.right)
● 遍历算法
通常遍历，我们希望做的是对每一个节点执行一个类似的遍历单元操作。下面以深度优先的遍历，中根序为例，
def preorder(t, proc): # proc是一个遍历处理函数，对每个节点做操作 if t is None: return proc(t) preorder(t.left, proc) preorder(t.right, proc)
这是一个简单的遍历函数的示例，实际运用过程中我们还可以进行中根序后根序的遍历，只要调整函数体中调用preorder和proc的顺序即可。另外如果要实际写这么一个功能的函数，通常还需要一些要素比如检查t是否是一个合法的二叉树对象等等。
如果基于这样的遍历思想做一个简单的应用，那么我们可以考虑设计一个打印树结构的函数。这里说的打印不是说纵向上的打印（那种还要考虑当前层有多少节点，节点之间间距如何安排等问题），而是简单地构造出一个类似之前list实现方法时的样子。代码如下：
def print_BinTNode(t)： if t is None: print('^',end='') return print('('+str(t.data),end='') print_BinTNode(t.left) print_BinTNode(t.right) print(')',end='')
*这里代码用的是Python3了。主要考虑到可以指定end参数，这样打印的时候就不会很恶心地一行一行都分开了。
比如二叉树实例 BinTNode(1,BinTNode(2,BinTNode(5)),BinTNode(3))调用这个方法的话得到的就是(1(2(5^^)^)(3^^))。遇到没有子树的情况，并不是直接跳过而是输出^字符。这主要是考虑到，当只有一个子树的情况，如果不打印^的话会导致最终打印出的结构中，无法判断单独的子树是左子树还是右子树。
接下来实现二叉树的宽度优先遍历。宽度优先需要一个队列作为栈记录尚未处理的其他节点的信息。之前在用list实现二叉树（或者把二叉树看做是一个list的时候）其实宽度优先遍历就是对这个list的简单顺序遍历。而我们现在在处理的东西变成了二叉树类的对象，因此需要一定的调整。
def levelorder(t,proc): qu = SQueue() qu.enqueue(t) whie not qu.is_empty(): t = qu.dequeue() if t.left is not None: qu.enqueue(t.left) if t.right is not None: qu.enqueue(t.right) proc(t.data)
SQueue是一种FIFO队列，每来到一个子树，先从队列中拿出这个子树对象，先判断其左子树和右子树是否存在，存在则入队，然后再去处理这个子树根节点的数据，然后进行下一个同层or下一层子树的处理。
接下来说一下非递归的深度优先遍历。前面的递归深度优先遍历很好理解也很好写。如果强行非递归，那么就要在代码中引入一个栈了。大致的算法我们可以设想一下：
还是以先根序为例，首先我们处理一个树的根节点，然后左子树，然后右子树。左子树还好说，大不了再处理下左子树根节点就行了，右子树怎么办？因为它要在我整个左子树都处理完后再处理，所以先入栈。随后我们就可以安心处理左子树。此时处理左子树的流程也是这样的。以此类推的话，也就是说我们的整体流程实际上是先沿着树的最左边逐步向下，直到最左下叶子节点。处理完它之后，现在可以从栈中取出一个树。这个树应该是最左下叶子节点的兄弟右子树。那么这个树又该怎么处理，其实还是一样，沿最左边往下，走类似的流程。
最终，呈现为代码就差不多是这种感觉：
def preorder_nonrec(t,proc): stack = Queue.LifoQueue() while t is not None or stack.not_empty(): # 若t是None，说明上一个处理的节点没有右子树,此时就去看栈中是否还剩下没处理的子树 # 如果stack也空了，说明没有要再处理的东西了，因此可以直接给出结果 while t is not None: # 这个循环其实是从某个节点一直沿着最左边走下去 # t为None表示上个处理掉的节点已经是最左下的节点（没有左子树）此时可以跳出循环，获取上个节点的右子树处理 # 每跳到一个右子树，其实流程一样，还是沿最左边往下走 proc(t.data) stack.put(t.right) t = t.left t = stack.get()
* 估计也不会有人看到这里，可能我自己都不太会…我想记录一下现在的心情。最近心里乱的很，听着アヤノの幸福理論有种回到大一的感觉，迷茫焦躁，对未来充满畏惧同时也没有勇气向前一步。细想起来，突然冒出想去日本留学的念头，好像是因为在jcinfo上面遇到了不少坚定去日本留学的中国学生和坚定来中国留学的日本学生。然后略微深入地了解了下，发现留学的成本并没有我想象得那么高，反过来，以我已有的成绩，不去留学一下反倒觉得有些可惜。就在这样一种神奇的心境的驱动下，这两天发疯似的收集留学相关的信息，就好像明天就要去留学了一样，可笑的是时时刻刻内心深处又有一个小恶魔在提醒我现实是什么样的。它让我觉得我就像是一个小丑，为了逃避现实而好高骛远，向四周宣称着我那不太可能实现的计划。尤其是写到这个算法的时候，我想小小考验下自己看能不能独立写出来，但是没想到在有教科书的文字提醒下，我还是写了个错的算法，而看到书上的算法才深知自己没有这方面的才能。。可是又能怎么办呢，入了这一行了。留学这两个字背后，我看到的是金钱，能力，未来可能要付出的辛苦，各种各样的阻碍和困难；鼓励别人的时候，一句简单的“加油”多轻松啊，可是谁又能知道这背后需要多么复杂的纠葛和心绪。
感觉很对不起爸妈，在家里处于这种情况的时候又半分心血来潮地说出这种话，将他们好不容易整理好的情绪又打乱。但是我的内心却又真的是很想实现这个愿望。差不多也该回家了，剩下的我想写到日记本上。
昨天好像是有点累了的缘故吧，整个人都变得很悲观。今天一觉醒来感觉好些了，虽然目标仍然很远，但是努力开始吧。
下面这个是非递归的中根序遍历，是我自己写的，也不知道对不对… 大概思想是将右子树和根节点分别先后入栈。当沿最左边一直处理到左下角之后，再回头到栈中取出内容进行处理。由于栈中混合保存着根节点数据和右子树两种形式，所以还需要有个is_data()方法判断，如果是根节点的数据，那就proc一下。由于可能存在某节点的父节点没有右子树，此时处理完父节点数据后，栈中的下一个就是父父节点的数据而非父节点的右子树，所以在处理数据那边又加了一个循环，直到栈中取出的不是单纯数据而是树时，再赋值给t，回到上一层循环，去处理获取到的这个右子树。
def midorder_norecursive(t,proc): stack = Queue.LifoQueue() while t is not None: while t is not None: if t.right is not None: stack.put(t.right) stack.put(t.data) t = t.left ele = stack.get() while ele.is_data(): proc(ele) try: ele = stack.get() except Queue.Empty,e: ele = None t = ele
接下来再来看看非递归的后根序序列。稍微改造下上面的中根序函数，比如修改一下t.right和t.data入栈的顺序，就可以实现后根序了。（非常不确定是否正确… 我自己试了几棵树都可以，但估计还有一些漏洞没注意到）。下面的函数则是书中给出的一种解决方案。
def postorder_norecursive(t,proc): stack = Queue.LifoQueue() while t is not None or not stack.empty(): # 1. t是None可能是右子树处理完了或者没有右子树 # 2. 栈为空表明已没有未处理的内容，可以结束程序 while t is not None: # 沿着最左边（不是严格地了）先入栈一批子树 stack.put(t) t = t.left if t.left is not None else t.right # 这个表达式不同于之前的入栈策略，是有左子树则左子树入栈，否则若有右子树，右子树也可入栈。 t = stack.get() proc(t.data) if not stack.empty() and stack.top().left == t: # 1. 如果栈为空，则表示没有需要剩余需要处理的内容，可以返回了 # 2. 目前t是栈顶的左子节点，说明其右子节点还没有处理。因为后根序，先去处理右子树。 t = stack.top().right else: t = None
入栈策略发生变化的主要原因，是因为在先根序中，很明确沿着左分支下行并将所有右分支都入栈，总体而言覆盖到了整个树。但是在这个场合中，结合下面的子树处理逻辑，如果某节点没有左子树，相当于其没有了访问右子树的钥匙（右子树的访问一定要通过其兄弟左子树，在if stack.top().left == t这个入口进行访问），所以要把左子树为None的情况单独拎出来维护到栈里。
● 生成器构造遍历函数
这是一个小点。上面的遍历函数其实是给了proc做了一个处理。但很多时候，我们会希望通过遍历获取到树的线性序列形式。此时，生成器就是一个很好的方案。但是用yield在这里有个坑，之前在Python的生成器学习文章中也提到过，就是在递归的时候，yield获取到的单个数据是只保存在本层递归的函数调用栈中，并不会自动充入到上层递归的调用栈里。如果是这样的话，那么就需要进行一些特殊处理才行。当然非递归情况就很方便了：
def preorder_elements(t): stack = LifoQueue() while t is not None or not stack.empty(): while t is not None: stack.put(t.right) yield t.data t = t.left t = stack.get()
如果是递归，那么可以这样：
def tree_elements(t): if t is None: return yield t.data for data in tree_elements(t.left): yield data for data in tree_elements(t.right): yield data # 这里就不能只是tree_elements(t.left)，否则这只是在这里声明了一个生成器，其中内容保存在各自层递归的调用栈中，最高层的调用栈无那些内容
● 非递归遍历的复杂度
光看某个具体算法的程序可能比较难看出来算法的复杂度，但从一个更加宏观的视角来看待，整个树的所有节点都是只被访问一次，不考虑proc函数的具体复杂度的话，那么遍历整个树的时间复杂度就是O(n)。空间复杂度根据具体算法不同可能不同。如果出现的是比较极端的那种单线条树，比如最左边全部都有一个右子节点且是叶子节点的情况，这棵树本身的空间复杂度达到O(n)（高度具体值是n/2，也是O(n)量级的），而先根序遍历的时候所有的右子树有都要入栈，所以栈的大小也到达n/2，即O(n)的。
■ 真·二叉树类
上面基于树节点的二叉树类（本身也就是节点类）在写出来的时候就具有了递归结构。表现形式上其实和list实现的差不多。另外还有一些小问题比如空树用None表示，并不是二叉树类。解决这些问题的方法就是在这个基于节点的构造外面再包一层真·二叉树类，做一个更高层次的封装而把节点的那种结构维护在实例的内部。
目前还没太搞明白这样一个类的用法，姑且给出书上的定义：
class BinTree: def __init__(self): self._root = None def is_empty(self): return self._root is None def root(self): return self._root def leftChild(self): return self._root.left def rightChild(self): return self._root.right def setRoot(self, binTNode): self._root = binTNode
可以看到的一个特点是，这个类没有涉及到类似于getParent()的方法，即无法获取到这个树实例的父节点在哪里。要想实现这一点可以考虑将BinTNode类扩充一个self.parent属性，这样相当于一个节点拥有self.root,self,left,self.right和self.parent共四个属性。
【哈夫曼树】
■ 定义
之前我们讲到过一种二叉树叫做扩充二叉树。把任意一颗二叉树补充称满二叉树的话，那么树就变成了一棵扩充二叉树，新补充上去的那些节点叫做外部节点。扩充二叉树的一个属性叫做外部路径长度，指的是从其根节点开始到所有外部节点的路径的和。显然，外部路径长度E = (l1+l2+l3...+lm)，其中m是外部节点的个数而ln代表根节点到特定外部节点n的路径长度。
现在我们考虑为每个外部节点赋一个权值。，这样可以得到一个属性叫做带权扩充二叉树外部路径长度。以WPL表示。这个值WPL = (w1l1+w2l2+...+wmlm)。 w1,w2...wm是指从第一个外部节点开始到第m个外部节点的所有权值。比如下图的两个树的WPL值：
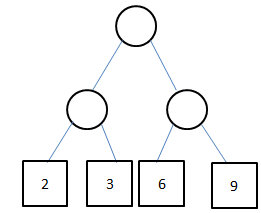
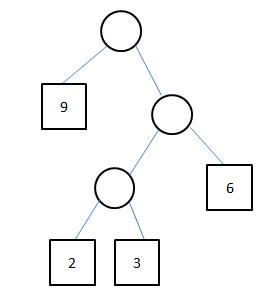
左边的树WPL = (2+3+6+9) * 2 = 38，右边的树是WPL = 9+(6*2)+(2+3)*3 = 36。
好，现在来看下定义。如果我的手上有一个实数集合W，其中有实数w0,w1,....,w(m-1)。将它们作为外部节点的权值，填充到一颗扩充二叉树的外部节点中。显然这样的二叉树形态有多种多样的。其中一种二叉树样式T可以做到WPL值最小，此时我们把T称作结合W上的最优二叉树，或者哈夫曼树。
以上面两个两个树为例，对于同样的数据集{2,3,6,9}，左边树的形态和右边树不同。而对于一种形态来说，不同的权值安排也会导致WPL值的不同。实际上，右边这种形态和这种权值安排方法是WPL值最小的，所以右边这样一颗树是{2,3,6,9}的哈夫曼树。
■ 构造
构造哈夫曼树的算法就叫哈夫曼算法。首先可以明确，哈夫曼算法的输入是一个实数集W，最终要生成的是W对应的哈夫曼树。其大概描述是这样的：
首先将W中元素看成是只有一个根节点的小树，然后一字排开，他们都将作为最终哈夫曼树的外部节点。选择其中根节点值最小的两个树（如果最小值有重复则任选两个即可，这也表明一个实数集W的哈夫曼树并不唯一，但是所有哈夫曼树的WPL都应该相等），通过一定手段将它们放到相邻的位置，然后将它们分别作为左右子节点，在他们上面构造一个根节点。根节点的值取两者的和。根据哈夫曼树的定义，这些非叶子节点的值并不计入WPL计算，这里只是做一个辅助作用。
通过这样的一次连接操作，我们将原数据集中的两个元素构造成了一个小树。现在将原有的两个原生元素去掉，再把这棵新的小树加入集合。接下来，将新加入的小树作为集合的一员，然后重新执行上述操作。选择两个值最小的树（刚才的小树也可以加入比较了），放到相邻位置，构造新树… 如此周而复始，最终集合中会只剩下一个树，此树就是集合W的哈夫曼树。
要证明这样的算法得到的确实是哈夫曼树有些困难，但是可以注意到，哈夫曼树的任意左子树和右子树交换位置，得到的仍然是哈夫曼树（构造新小树时并未指定两个已有树哪个在左哪个在右）。
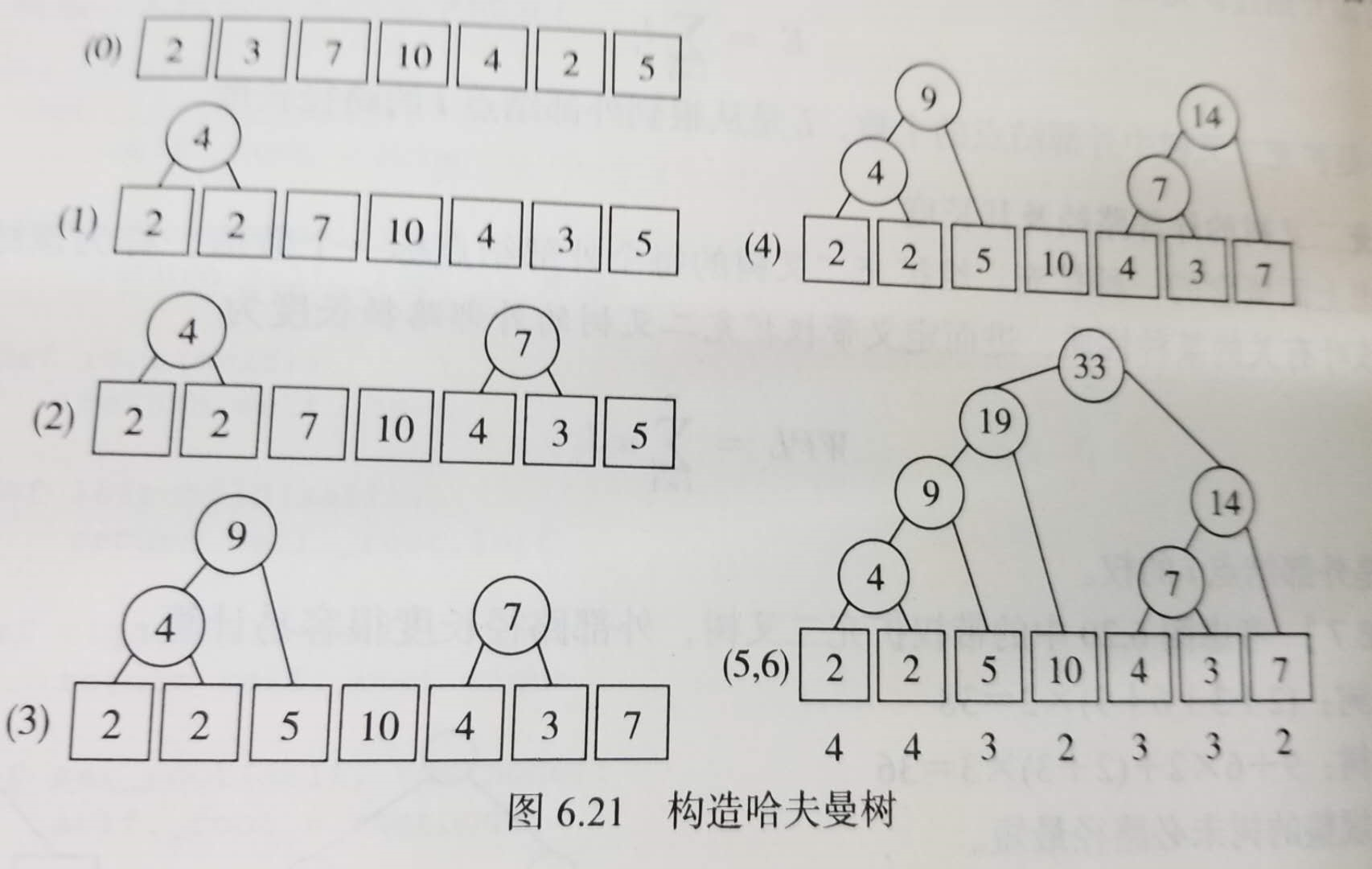最后一幅图中下面的数字是各个外部节点的路径长度
■ 实现
上述描述略复杂一些，具体编码实现的时候还可以设计一些更合理的逻辑，来去掉一些不必要的步骤。书上是这样设计的一个算法：
构造过程的两个关键点是1. 找到集合中两个最小树；2. 判断集合是否只剩下一棵树。对于第一点，我们可以构造一个定根节点值为优先值的优先队列，这样每次只要在队列前头取出两个值，得到的就一定是最小树，直接构造即可。至于第二点更简单，只要给这个优先队列实现一个统计还有多少元素的方法就可以了。
结合之前已经实现过的一些类，可以写代码如下：
class HTNode(BinTNode): def __lt__(slef,othernode): return self.data < othernode.data class HuffmannPrioQ(PrioQueue): def number(self): return len(self._elem)
有了类定义作为基础，很方便地就能写出Huffmann树的构造过程了。
def HuffmannTree(weights): trees = HuffmanPrioQ() for w in weights: trees.enqueue(HTNode(w)) # 构造完了优先队列，下面开始正式哈夫曼树的构造 while trees.number() > 1: t1 = trees.dequeue() t2 = trees.dequeue() newTreeRoot = t1.data + t2.data newTree = HTNode(x,t1,t2) trees.enqueue(newTree) return trees.dequeue()
下面来简单看一下哈夫曼树构建过程的复杂度。假设实数集weights中有n个元素。这里主要是两个循环，第一个循环如果采用的是构建堆，然后基于堆排序进行优先队列的构建，那么复杂度是O(n)，这里代码默认采用的是一般的基于列表的优先队列，即enqueue一次的复杂度是O(logn)，总共进行n次，所以这里的复杂度是O(nlogn)的。
第二个循环进行了n-1次，而里面主要耗时的部分也是enqueue的O(logn)，所以第二个循环也是O(nlogn)的。因此总的时间复杂度就是O(nlogn)。至于空间复杂度，最初的队列有n个元素，后面虽然新增了很多不计入WPL统计的节点，但是整棵树最后的总结点树是2n-1个，所以是O(n)。
■ 哈夫曼树的重要应用
其实哈夫曼发现了这种算法的契机，是为了要做出一种哈夫曼编码。我们知道通讯的时候需要将文字信息转换为二进制编码进行传输。那么文字（比如26个英文字母）如何和一个二进制编码进行对应。但是这个对应还不是那么简单的。首先是功能上的考虑： 一个重要要求就是每个字母的编码都不是其他任何一个字母编码的前缀。比如A编码为0，B编码为01，那么当接收到型号01的时候，是翻译成A1还是B呢所以这个需要进行考量。第二点是性能上的考虑，即如何让同样多的二进制数据中传递更加多的信息。一个优化方法是找到字母中词频（对应哈夫曼树中的权值）相对高的比如E，S等字母，将它们编码得短一些；对于不常用的X，Z编码得长一些，这样总体可以加快信息收送效率。
哈夫曼树正是解决了上面两个问题的一个解法。这也是哈夫曼树重要的应用，而得到的编码对应关系就是所谓的哈夫曼编码了。
首先，我们将需要进行哈夫曼编码的所有字母一字排开并且赋予它们各自的权值（即出现词频，通常可以通过词频概率或者单纯的出现次数），基于这个权值进行哈夫曼树的构造。构造完成后，从整棵树的根节点开始给每一个树连接到左子树上写0，连接到右子树上写1。从根节点出发，沿着路径走到某个叶节点，将一路上的0和1连接起来组成的二进制数，就是本叶子节点对应字母的编码了。
通过哈夫曼树得到的哈夫曼编码，可以保证1. 不同编码之间不会存在一个是另一个前缀，从而引起信息解读混乱的问题 2. 高频的字母编码尽量短
具体实现写在下面（只能想到一些笨办法…），简单来说就是将各个字母和各自的频度作为一个tuple的两项，然后整个tuple作为节点的值保存。由于最终要获取到根节点到各个叶子节点的路径（且左右还有区别）所以要改造一下BinTNode类。我的办法是给节点类加上了parent和type两个属性。parent指向父节点，type可取值'l','r'或者None来表明这个节点属于父节点的左右节点还是这个节点没有父节点。
因为优先队列涉及到节点之间比大小，所以还需要顺便重载一下__lt__方法。生成哈夫曼树之后，从根节点开始遍历，如果碰到了叶子节点，那么就从这个节点开始逆推到根节点的路径，并且根据type属性判断路径该加上0还是1，最终获得本节点对应的编码。由于节点数据维护了字母，也就得到了字母的编码。把所有的这些编码输出即可。逆推的时候由于parent节点都已经有了明确地址，所以单条路径就像链表的遍历一样，总长是O(logn)，总的来说逆推过程是O(nlogn)的（我想是这样吧…不确定对不对）
代码：
''' Heap，BinTree，BinTNode类前面实现过了，包括parent和type属性已经写在BinTNode类中 ''' class WeightTNode(BinTNode): def __lt__(self, other): return self.data[1] < other.data[1] def huffman(_dataSet): dataSet = [WeightTNode((item[0],item[1])) for item in _dataSet] heap = HeapQueue(dataSet) while len(heap) > 1: t1,t2 = heap.dequeue(),heap.dequeue() newNode = BinTNode(('',t1.data[1]+t2.data[1]),t1,t2) t1.parent = newNode t2.parent = newNode t1.type = 'l' t2.type = 'r' heap.enqueue(newNode) return BinTree(heap.dequeue()) if __name__ == '__main__': ofteness = {'a':12,'b':2,'c':5,'d':10,'e':11,'f':4,'g':3,'h':7} tree = huffman([(k,v) for k,v in ofteness.iteritems()]) code_map = {} for node in tree.preorderIter(): tmp = [] if node.left is None and node.right is None: # 到达叶子节点 char = node.data[0] while node.parent is not None: if node.type == 'l': tmp.append('0') elif node.type == 'r': tmp.append('1') else: raise Exception('!') node = node.parent code_map[char] = ''.join(reversed(tmp)) print code_map
【树】
二叉树说完这么多，接下来来看一下更加一般的树。相比于二叉树，一般的树去掉了每个节点最多只能有两个子节点的性质。但是树也有很多共性，之前在讲二叉树的时候觉得理所当然的东西，这里再重点提要一下。
1. 树具有较为明显的层次性
2. 只允许高层元素对低层元素有关，不允许逆向关系，也不允许任何非垂直方向的关系。即同层元素之间互相独立无关系
上面用了很多的“圆圈直线”表示树是一种很常用的方法。小学奥数中常用的韦恩图也可以用于这种表示上下层级包含的关系。
很多概念都和二叉树类似，就不多说了。比较不同的是，泛泛的树对于子节点的顺序可以考量也可不考量。当不考量的时候这种树是无序树，反之则是有序树。但是一个坑是，最大度数为2的有序树并不是二叉树。子节点有序并不意味着子节点一定要是左子节点或右子节点。所以说，二叉树中当一个节点只有一个子节点的时候必须指明它是左子节点还是右子节点；而在最大度数为2的有序树中，一个节点只有一个子节点的时候可以不管其是左还是右。
由于在计算机中的存储本身就是有顺序这个特点的，所以在数据结构中主要考察的都是有序树这一类。
树林是指若干棵互不相交的树的集合。因为只需要满足不想交即可，所以一棵大树的各个子树也可以组成一个树林（这也是常见的研究方法，毕竟研究完全独立的几棵树之间的关系意义不大）。根据有序和无序性，树林也可以分成有序树林和无序树林。
下面就是一个神奇的事情了： 任意一片树林，都可以一对一地转化成一棵二叉树。要做的操作是这样的：
1. 将树林中各树的根节点水平对齐后一字排开。
2. 将各树中所有同一层中拥有同一个父节点的兄弟节点连接起来，另外将所有树的根节点也看做是同一层的兄弟节点，全部连接起来
3. 同层的兄弟节点中，除了最左边的一个，其余连向父节点的所有连线都去除。由于2中有兄弟节点之间的连线，所以不会有节点孤悬。
4. 将所有2步骤中添加的连线看做是父节点和右子节点之间的连线，所有原来就存在于树中的连线看作是父节点和左子节点之间的连线。以左边第一棵树的根节点作为整个新二叉树的根节点
这样就将原先的树林改造成了一棵二叉树。
反过来，如何通过二叉树还原一个树林。步骤是：
1. 如果碰到某个节点C0，其有左子节点C，且左子树含有最右边，则这条最右边上的所有节点C',C'',C'''...都和C0进行连线
2. 去除二叉树中所有连向右子节点的边
可以注意到这样的分隔只要二叉树有右子树，那么这样一颗二叉树就可能被分成多棵树，即形成树林。再说一次，这样的树林和二叉树之间是一一对应的。
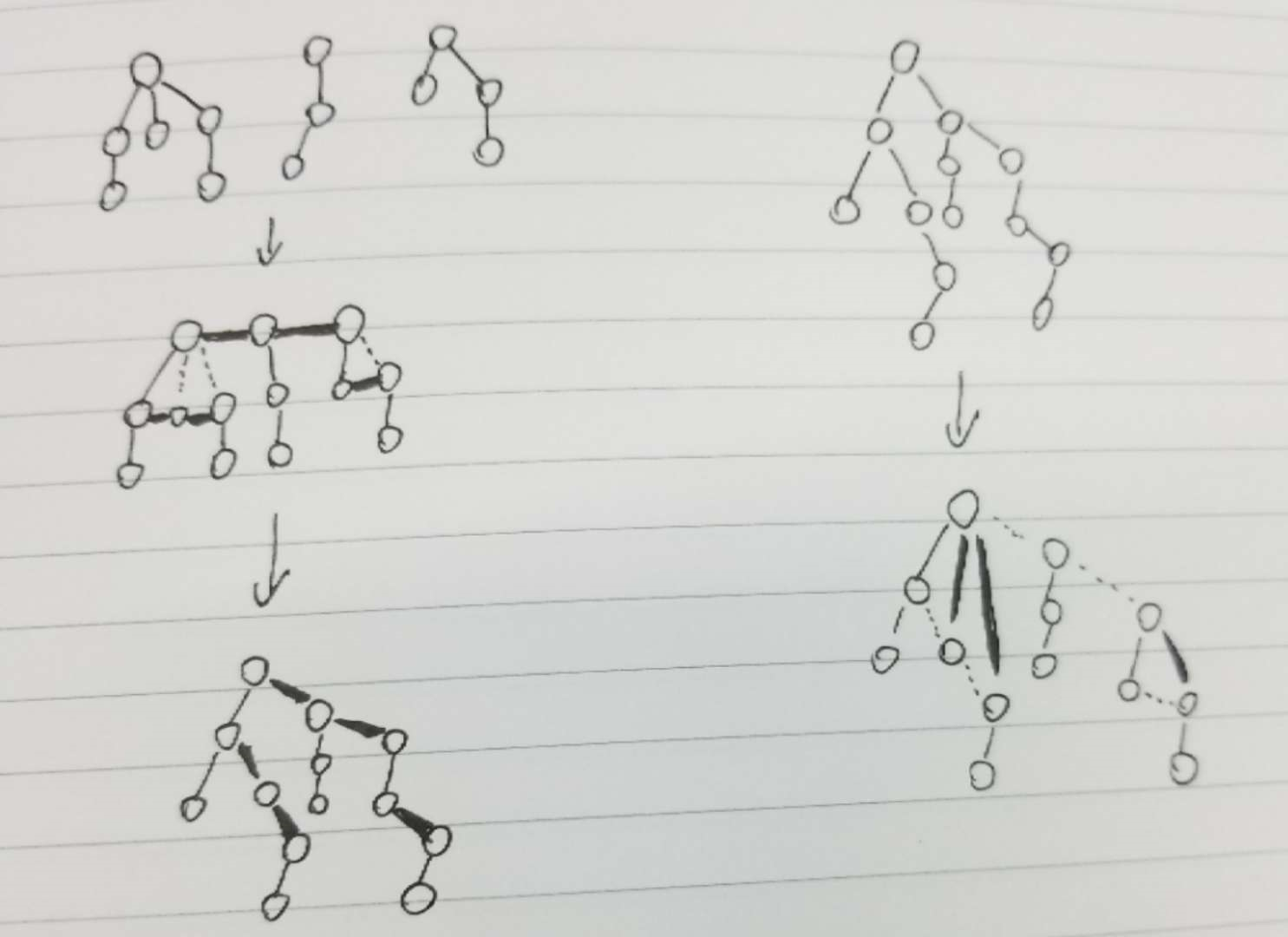左边是树林变二叉树，右边是二叉树变树林。虚线是去掉的线，粗线是过程中新加的线
■ 树的普遍性质
直接泛泛地讨论树意义不大，可以稍加限制比如定义树的度数k。一棵树的度数为k表示这棵树的任意一个节点，最多只能有k个子节点。因此可以得到下面一些关于树比较普适的性质。
1. 树的第i(i>=0)层至多有k^i个节点
2. 度数为k高为h的树中，至多有 (k^(h+1) - 1)/(k-1) 个节点（等比数列求和）
以上“至多”的情况的树也是k度完全树
3. n个节点的k度完全树的高度是不大于logk n的整数
4. n个节点的树中有n-1条边
一棵树的抽象数据类型和二叉树的抽象类型十分相似，不过也有些出入的地方：
class Tree: def Tree(self,data,forest) def is_empty(self) def num_nodes(self) def data(self) def first_child(self,node) # 返回树中某个节点的第一个子节点 def children(self,node) # 返回树中某个节点的各个子节点的迭代器 def set_first(self,tree) # 用tree对象替代本树的第一棵子树 def insert_child(self,i,tree) # 将某棵树插入到i的位置 def traversal(self) # 返回一个可以遍历树中所有节点的迭代器 def forall(self,op) # 对树中所有节点执行op操作（通常一个函数）
其中较为重要的方法可能是如何进行树的遍历。其实一般树的遍历大体上和二叉树类似的。也分成宽度优先和深度优先遍历，深度优先也分成先中后根序的遍历。
比较有意思的一点，不知道还记不记得之前栈和队列那一片中曾经提到过基于栈和基于队列进行迷宫探索的时候，可以发现基于栈的探索是深度优先，而基于队列的探索是宽度优先的。其实在进行迷宫探索的时候整个逻辑流程走的就是一棵树的流程。这是一颗看不见的树叫做搜索树。基于队列进行探索时其实就是宽度优先地遍历这棵树，基于栈探索时就是深度优先（根据上次的具体实现应该还是中根序的）非递归的遍历。
■ 实现
一般树的实现，由于其结构不如二叉树那么有规则，可能会牵扯到很多麻烦，因此要根据树来选择适当的实现形式而不是简单地套用一个数据结构。下面介绍几种书上提到的
● 子节点引用表示法
这个方法其实是对二叉树线性表实现的一个扩展。有一个先决条件，那就是针对最大度数固定为m的树。首先，每个节点还是有存储数据的地方，其次它还有一块空间用来记录我这个节点有多少个子节点，因为最大度数是m，所以这个值不能大于m。然后再在这个对象中开辟新的m-1块子空间用来存放树。对于放不满的情况，那些多出来的空间就让它放着。
这种方法的优缺点也很显然，优点是数据结构比较规整，取数据很方便；缺点就是可能存在大量的被浪费的空间。
● 父节点表示法
父节点表示法的概念是创建一个连续表，这个表中的每个元素有两块空间，一块用来存储自己的数据，另一块用来指出其父节点的位置（比如位于这个数组中的下标值）。这样，只需要有O(n)的空间便可以将整个树完整地记录进内存当中。
当然这么做的缺点就是进行节点的增删查改时比较麻烦。因为这样的一个结构只允许我们从下往上地寻找关系，如果想要统一全局地考察树就比较麻烦了。
● 子节点表表示法
这种实现方法的意思在于创建一个连续表用来存储各个节点的数据，另外每个元素还需要有一块空间，用来关联这个节点的所有子节点的位置，比如在连续表中的下标。这个想法其实和父节点表示法类似，只不过每个节点的父节点只有一个，所以父节点表示法可以明确只使用O(n)的空间，而每个节点的子节点数目不定，所以子节点表表示法涉及的数据结构可能会更复杂。但是相对子节点引用表示法，其用了相对少的空间自上而下地维护了树的结构信息和数据信息。
■ 树的Python实现
下面的实现，核心上来说是一种嵌套列表的实现，有点类似于最开始我们基于List实现二叉树的那种。其实可以这么干是得益于Python本身具有了很多高级的数据结构可以直接使用。
我们将某个节点的子节点数据直接写在表示这个节点的列表中。当然如果是个子树那就是又一个列表。所以：
class SubtreeIndexError(ValueError): pass def Tree(data,*subtrees): return [data].extend(subtrees) def is_empty_tree(tree): return tree is None def root(tree): return tree[0] def subtree(tree,i): # 获取某个子节点/子树 if i < 0 or i > len(tree): raise SubtreeIndexError return tree[i+1]
可以看到，当我们严格限制Tree方法的subtree参数长度只能是2的时候，得到的就是一个List实现的二叉树了。
同时我们使用的Python列表结构的话，可以比较自由地扩缩容，也方便了树中节点的增删改。
然后根据二叉树中得到的经验，再稍微用类将这个嵌套列表给包装起来，成一个正式的树类
class TreeNode: def __init__(self,root,*subtrees): self._root = root self._subtrees = subtrees def root(self): return self._root def set_child(self,i,node): if i < 1 or i >= len(self._subtrees): raise IndexError self._subtrees[i] = node class Tree: def __init__(self,rootNode=None): self.rootNode = rootNode def is_empty(self): return self.rootNode is None def subtrees(self): for subtree in self.rootNode._subtrees: yield subtree def set_subtree(self,i,tree): if not isinstance(tree,'Tree'): raise ValueError self.rootNode.set_child(tree.rootNode)
长长一篇重要写完了。其实关于树这么大一块内容，还有很多很多书上都没提到，比如红黑树，线段树什么的。目前我也还是看不太懂这些内容… 要学的东西还有很多，很难有时间和精力再去进阶地深究一些内容，总之先这样吧。天也不早了，差不多该睡了。
