CFA - 投资学 - 3.资产配置:有效前沿曲线 Efficient Frontier,资本市场线 CAL
一、资产配置的类型
纵向配置:across time, 择时,不同的时间配置不同的资产。例如:先储蓄,再买房
横向配置:across assets,同一个时间上配置多样资产。
二、三步法 资产配置
分一下4种情况讨论;越往后越靠近真实世界。

情景一 : 1 risky, 1 risk-free

Step 1: 求出portfolio的总收益,期望收益,方差,标准差
portfolio的总收益 -- portfolio return
假设你总共只有1块钱,构建这样一个portfolio:其中w分钱去购买s&p 500指数, 1-w分钱去购买国债T-bill
rT 是国债T-BILL的收益率
rs 是s&p 500指数的收益率
rw 为portfolio的总收益
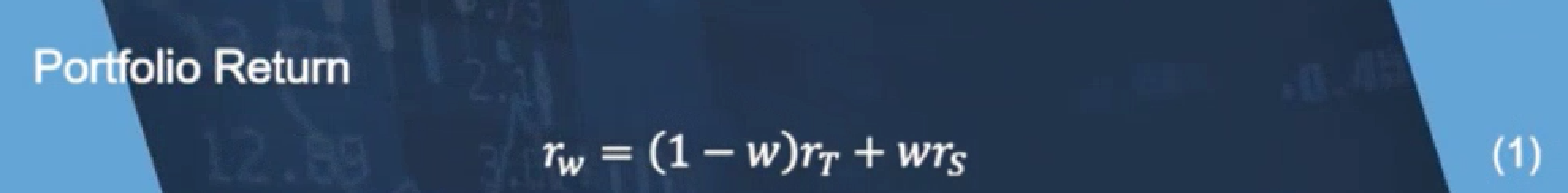
portfolio的期望收益 -- expected return
E(rw)是portfolio的期望收益
- 就是对公式(1)整体求期望。
- 由于T-BILL的期望收益固定,因此E((1-w)rT) = (1-w)rT
- 把括号拆开,合并同类项,得到公式(2)
E(rs) = 15.8% *0.7 -10.5% * 0.3 = 7.91%
E(rs) - rT = 7.91% - 5.5% = 2.4%
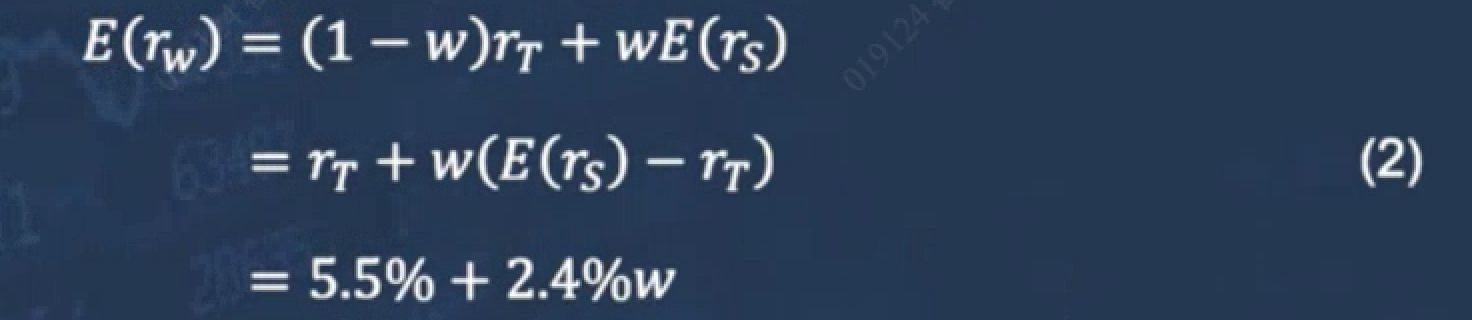
portfolio的方差和标准差
对公式(1)整体求方差。由于T-BILL固定收益,因此方差为零,能化简得到公式(3)
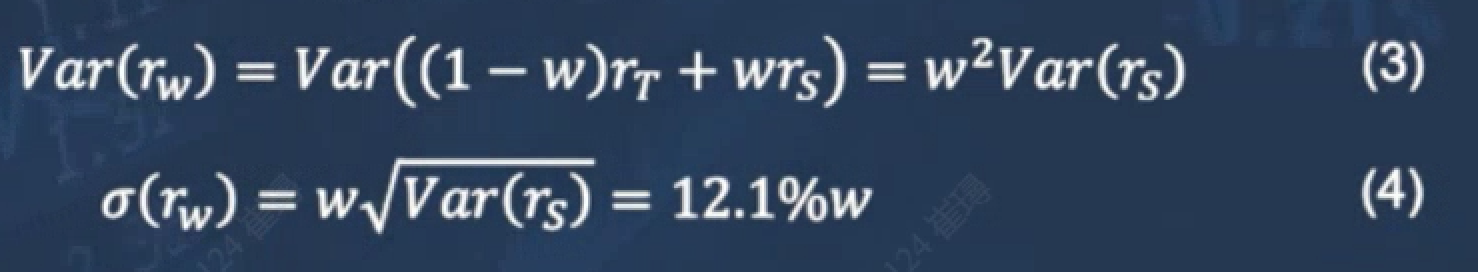
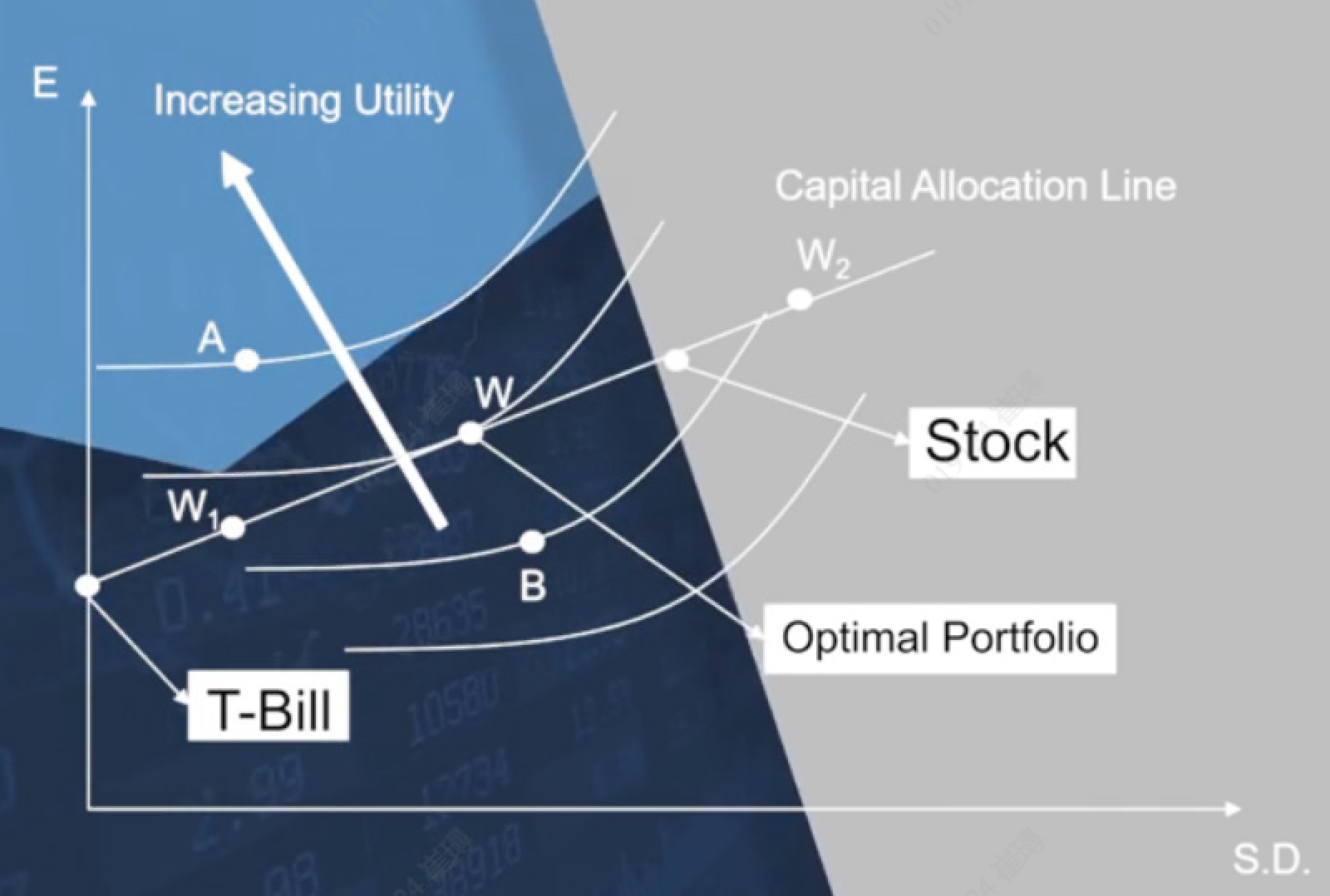
Step 2: 画出资产分配线 - Captital Allocation Line
前情提要:假设你总共只有1块钱,构建这样一个portfolio:其中w分钱去购买s&p 500指数, 1-w分钱去购买国债T-bill。w的取值范围[0,1]:
- 当w取值0,意味着所有的钱都去买了T-BILL。此时点位在T-BILL
- 当w取值1,意味着所有的钱都去买了S&P 500指数。此时点位在stock
这里的portfolio期望,是一个关于w的线性方程,该线成为资产分配线。我们的资产配置只能在该线上游走。
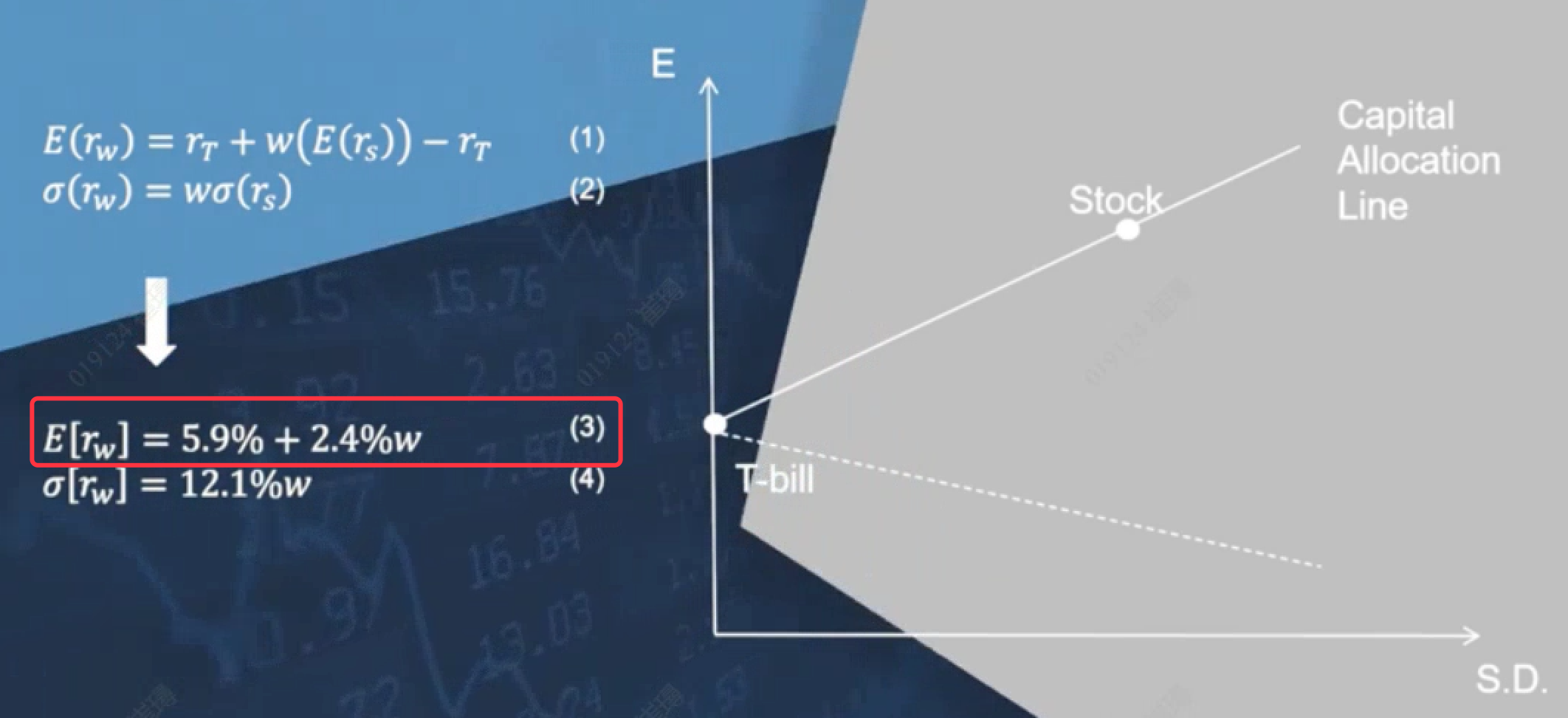
提问:什么时候能获得stock延长线上的点?
回答:拿出超过1块钱来投资。超出1块钱的钱,要通过借钱融资实现。
Step 3: 找出 效用无差异曲线 和 资产分配线 的切点,选出最优的资产组合
A资产:不能选择。因为其不再CAL线的取值范围
B资产:可以取到(其在CAL线下方),但其效用性还能继续提升,将其往左上方平行推动,去获得更大的效用Utility, 推到 效用无差异曲线 与CAL线有个切点W。
W资产:就是我们要找的最优资产组合,理由是:
- W在CAL上,是可得的
- CAL线上,任意一点的效用值,都没W点高。
明知道W资产是最优组合,但依然选择W1资产的是风险厌恶投资者;依然选择W2的是风险偏好更高的投资者
情景二 : 2 risky, 0 risk-free
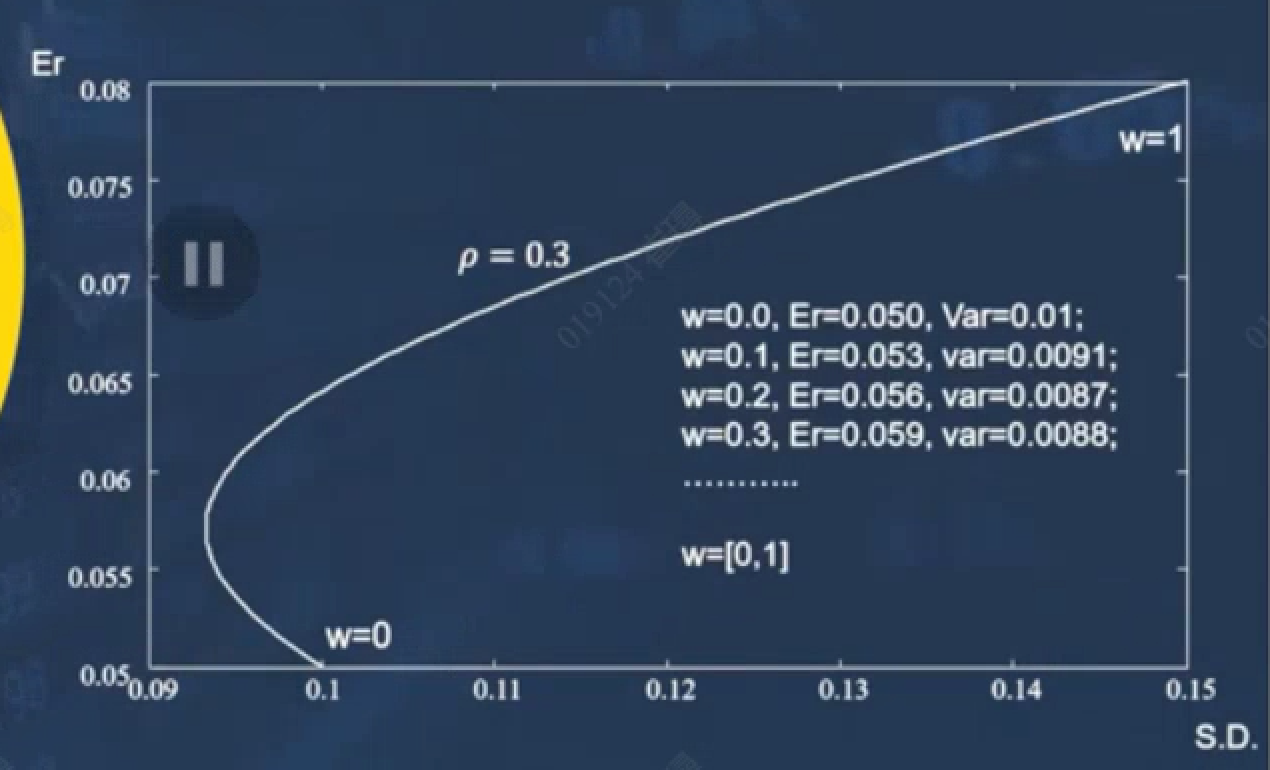
Step 1: 求出portfolio的期望收益,方差,相关性correlation
如果相关性等于1/-1,强正/负相关,那么期望收益还是关于w的线性关系(一条直线)
如果相关性不是1/-1,期望收益和w是二元一次方程的关系了。
例子:一个股票基金stock,一个债券基金bond

期望收益的W取值范围为[0,1]
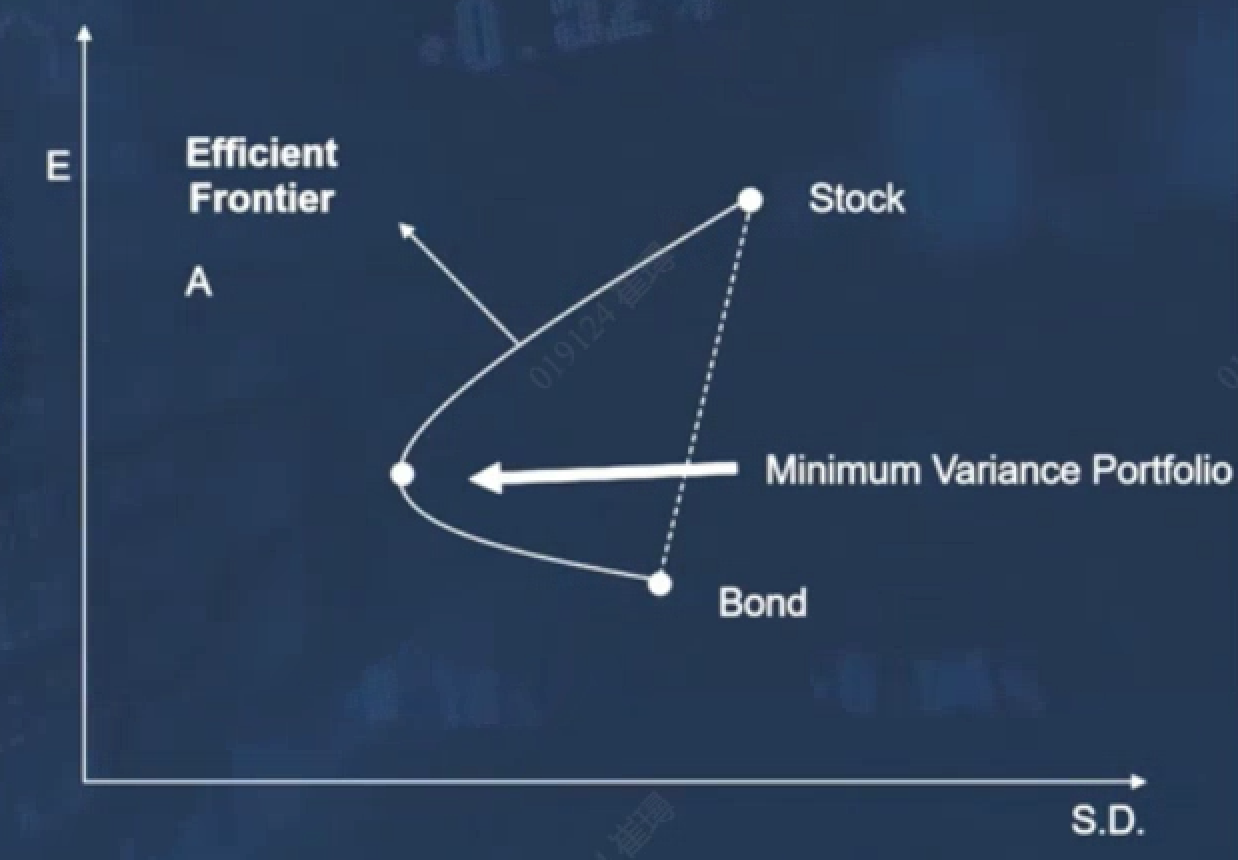
Step 2: 画出 有效前沿曲线 - Efficient Frontier
纵坐标E,收益
横坐标S.D. 标准差(这里数值越大,风险越大)
右上角 stock节点 是指全部配置股票基金
右下角 bond节点 是指全部配置债券基金
最左侧节点,是最小方差组合点,方差最小,风险最小 -- 以这个点横向切开:
- 下半部分的曲线,没人在这里设置portfolio,因为上半部分总能找到一个点具有相同的风险,但收益率更高的节点
- 上半部分的曲线,叫 有效前沿曲线 Efficient Frontier
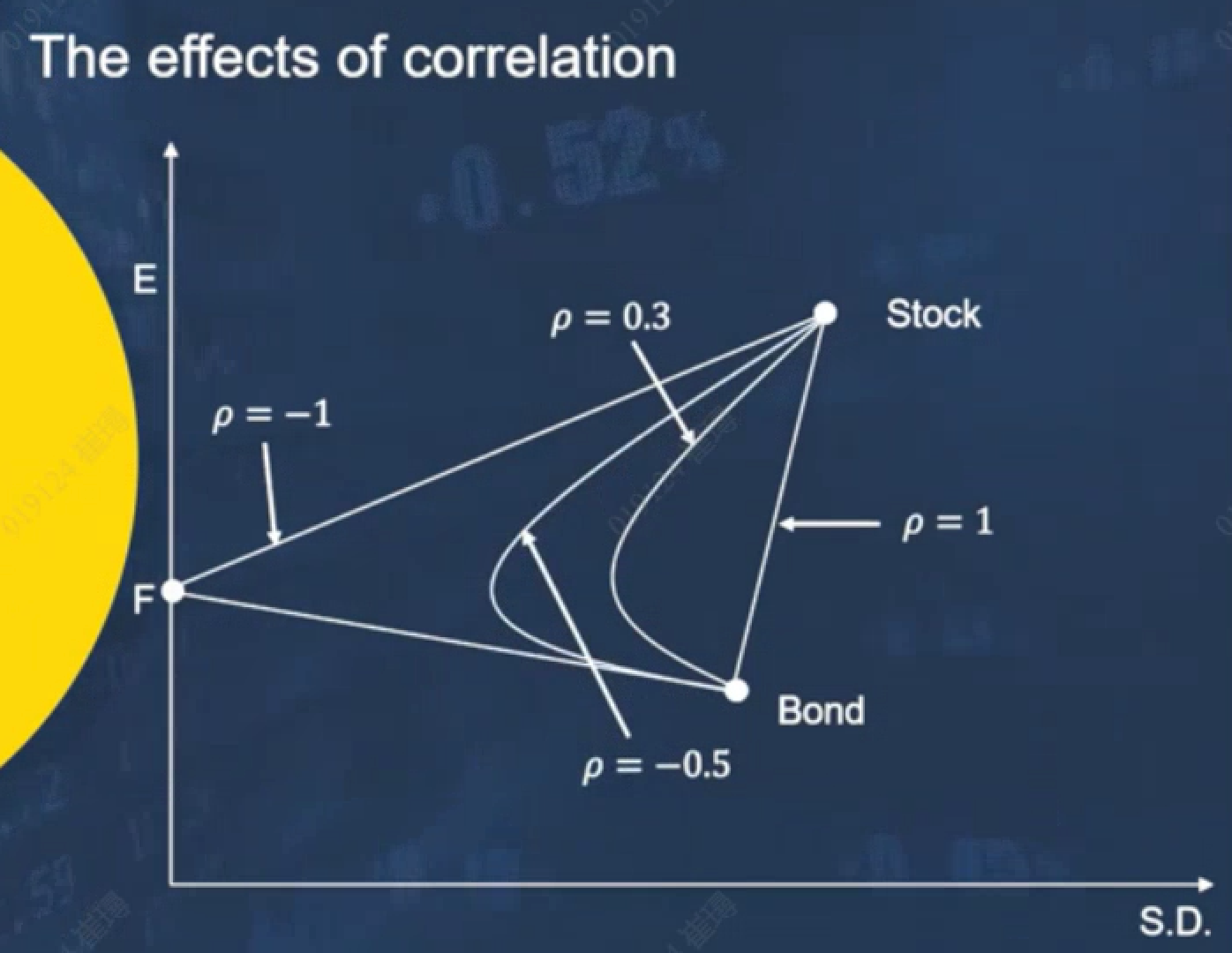
整个曲线向左弯曲的幅度,取决于两个产品的相关性ρ。ρ约小,弯曲幅度越大。
当ρ=1,是一条直线
当ρ=-1,是两个折线,汇聚在纵轴上 -- 风险降为0。说明我们把两个完全负相关的资产组合在一起,是可以完全剔除风险的。
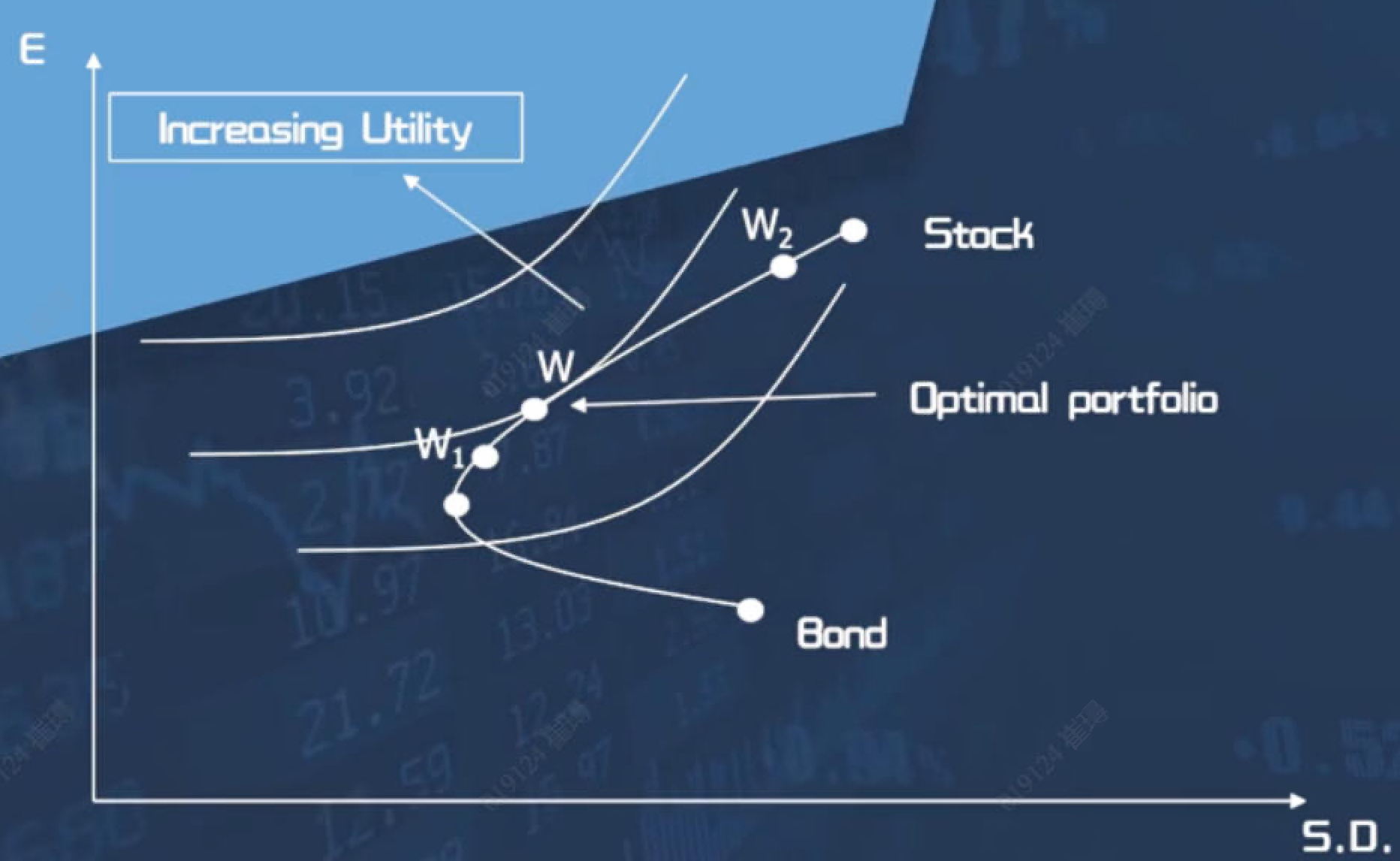
Step 3: 找出 效用无差异曲线 和 有效前沿曲线 的切点,选出最优的资产组合
切点W就是最优组合
明知道W资产是最优组合,但依然选择W1资产的是风险厌恶投资者;依然选择W2的是风险偏好更高的投资者
情景三 : 2 risky, 1 risk-free
Step 1,2 : 画出 可行集feasible set 曲线面积,找出 资本市场线 capital market line
先假设该情景只是2 risky, 0 risk-free,那么曲线应该和情景二的一样,是一条向左弯曲的曲线; 这时可以把这两个risky合并看待为1个risky
此时再加入无风险资产rf, 它一定是落在纵轴上。
那么此时就变成了情景一的样子,无风险资产和有风险资产产生的连线,都是可行集...
那么情景三:2 risky, 1 risk-free 的可行集,就是无风险资产rf这一点,向曲线的每一条曲线的连线组成的一个阴影面积!
最优资产组合,一定落在那条最高资产分配线上(阴影面积上面的边缘) --- 这就是 资本市场线 Capital market line
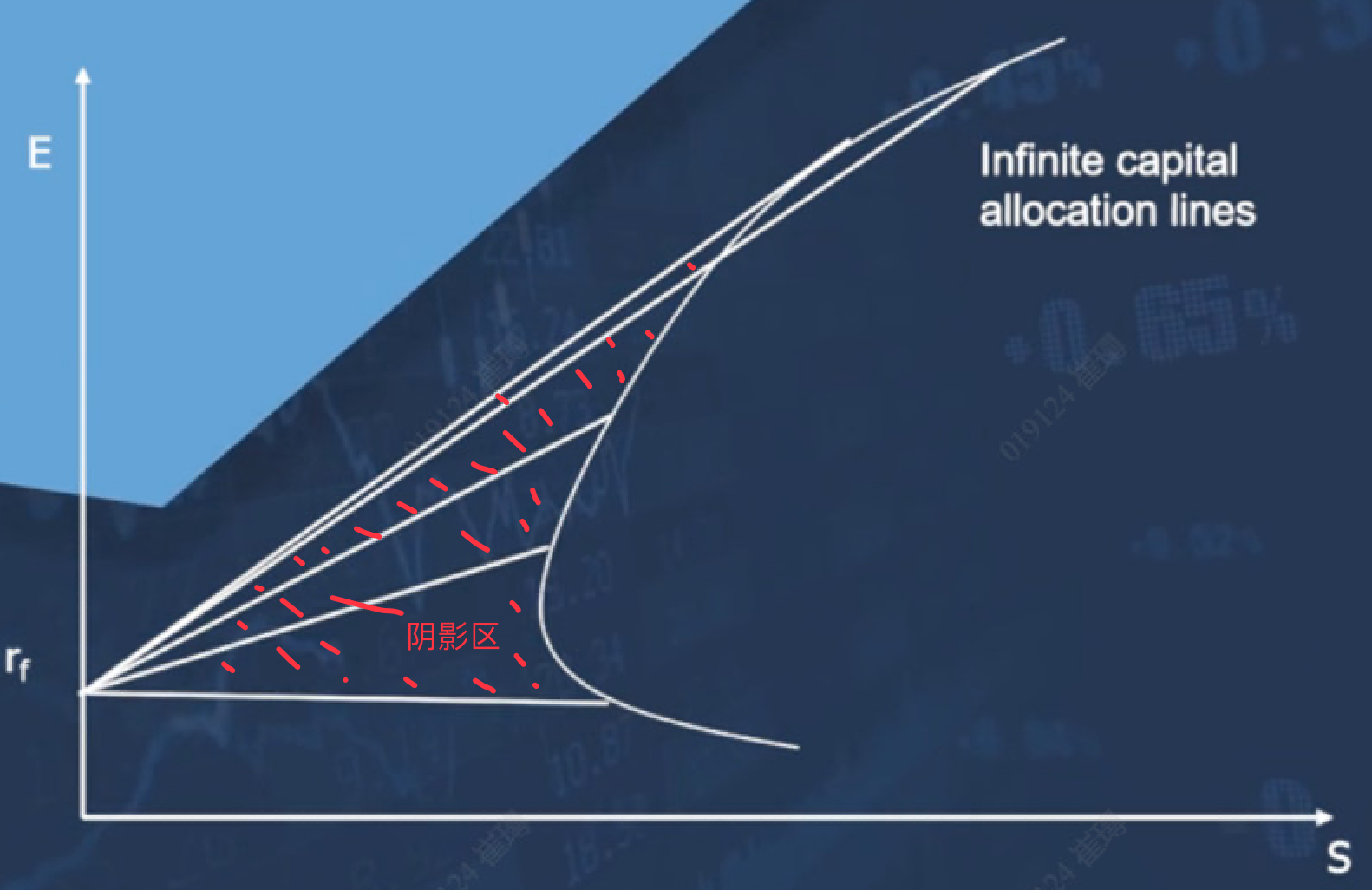
资本市场线 Capital market line
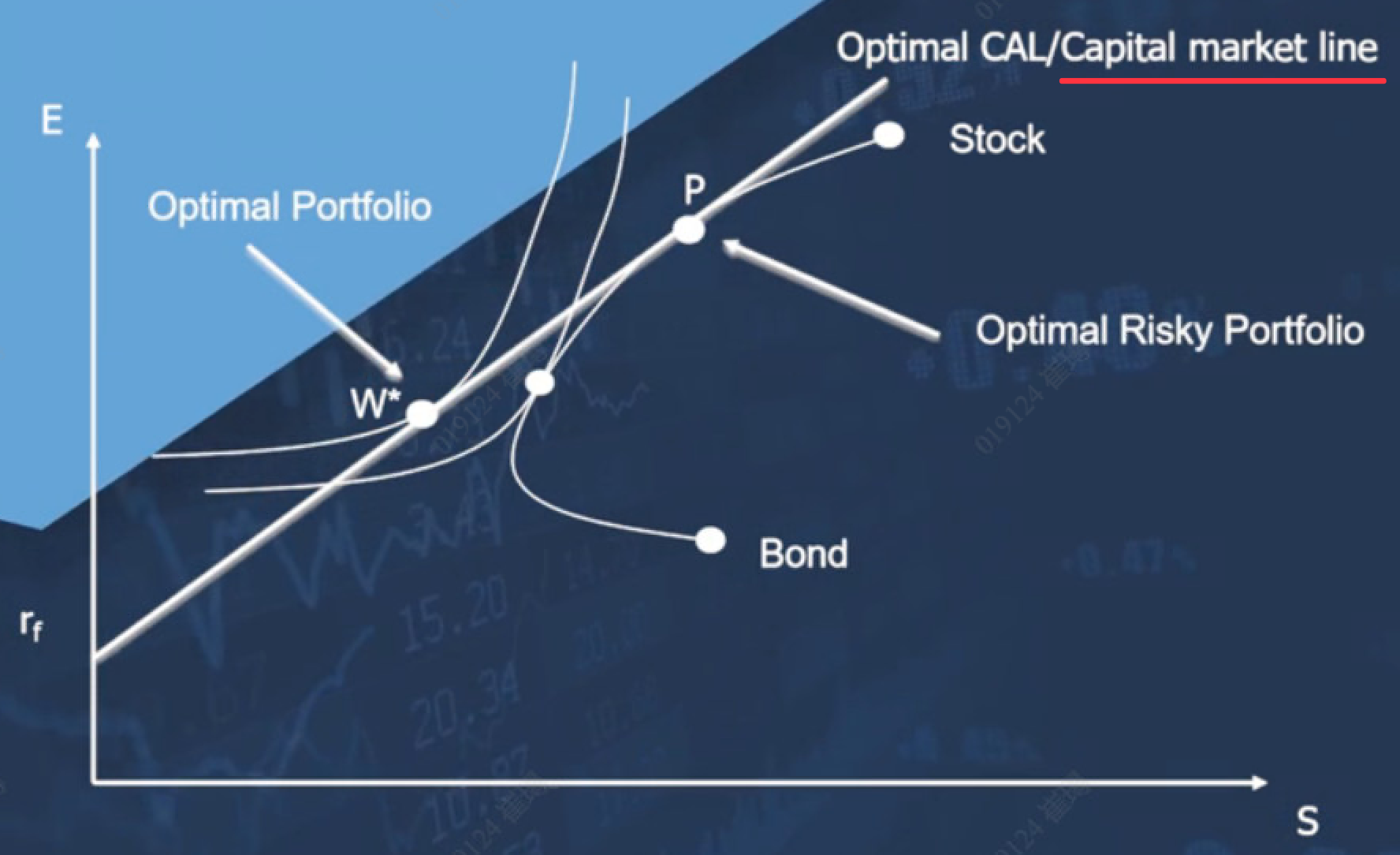
Step 3:找出 效用无差异曲线 和 资本市场线 的 切点,选出最优的资产组合
P点:给个特殊的名字,最优风险组合 -- 因为P点只是考虑了风险组合的最佳选择,并未纳入无风险资产所带来的益处。
黑点:是指在不包括risk-free资产时,只有两个risky资产的最优选择....其实就是情景二的情况
W*点:而当引入了risk-free资产后,带来了明显的好处。资本市场线 - capital market line 和更加左上方的效用无差异曲线有个W*切点。W*点比黑点的效用值更高。W*就是最优资产组合 - optimal portfolio。
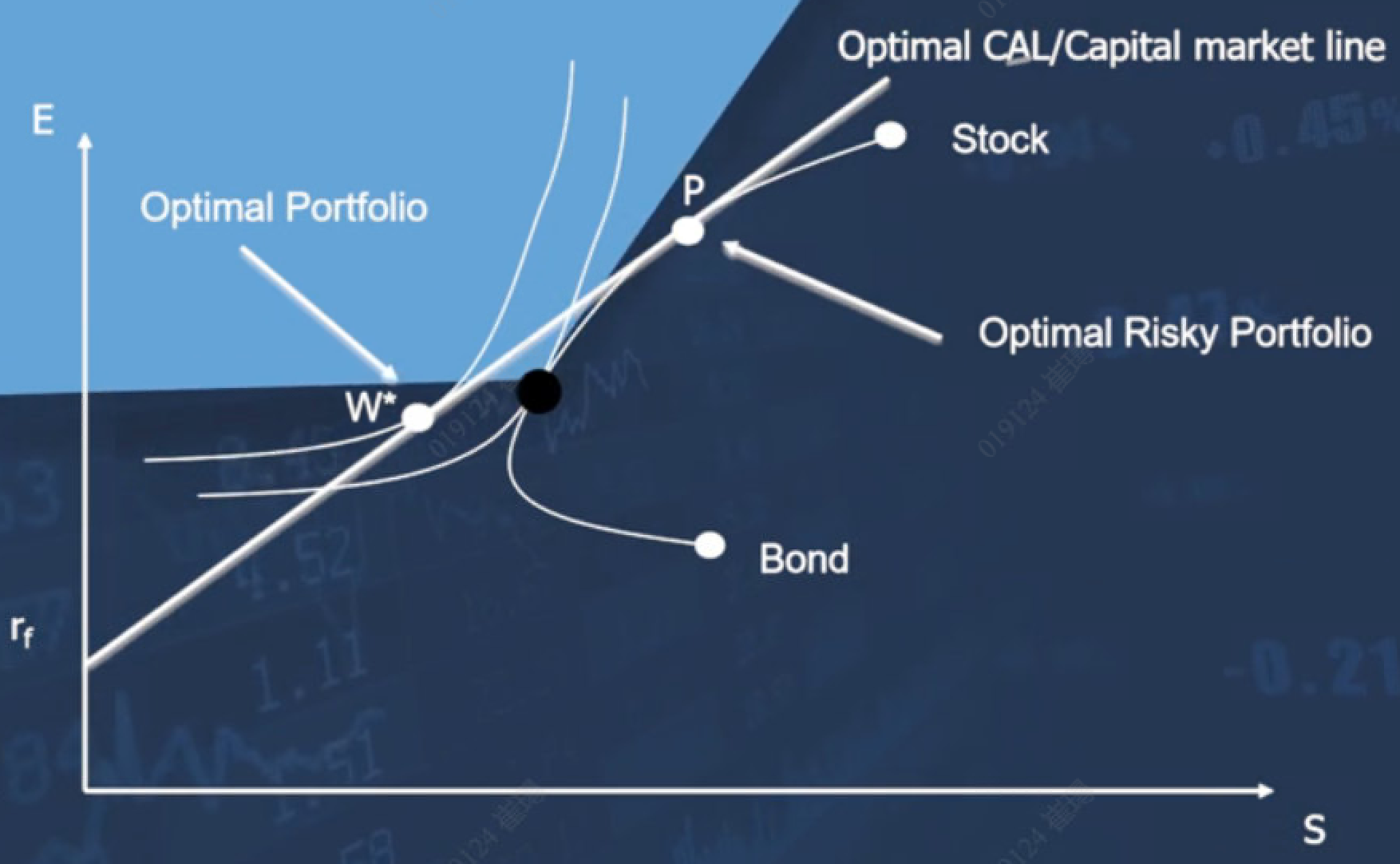
情景四 : many risky, 1 risk-free
many risky的可行集如图,依然是一个向左弯曲的一个面积
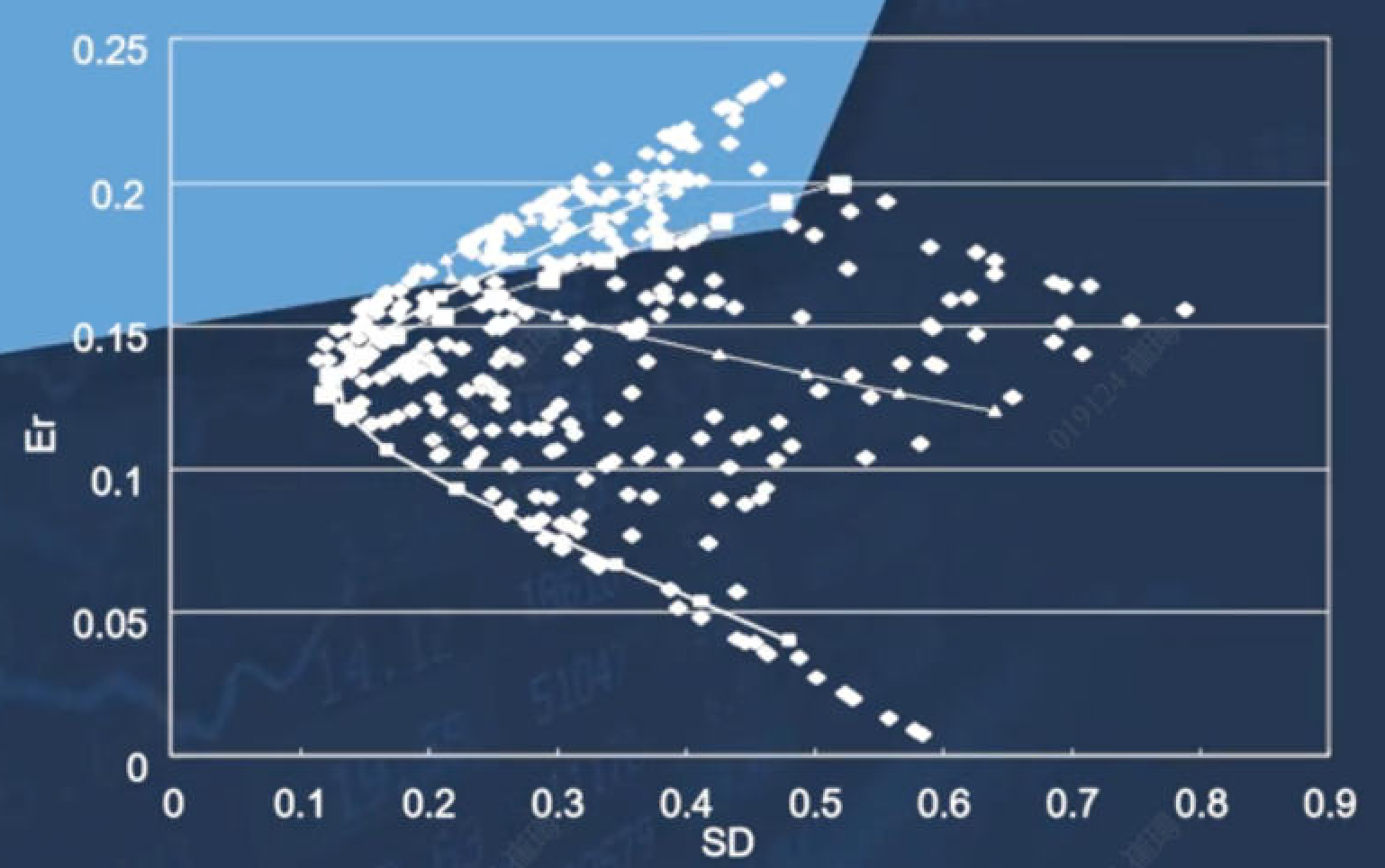
rf 无风险资产
P点,最优风险组合 -- 因为P点只是考虑了风险组合的最佳选择,并未纳入无风险资产所带来的益处。
红色的线,是资本市场线- capital market line
相对比蓝色的点 W',由于引入无风险资产rf, 我们可以把效用值推升到W点位 -- 红色的点
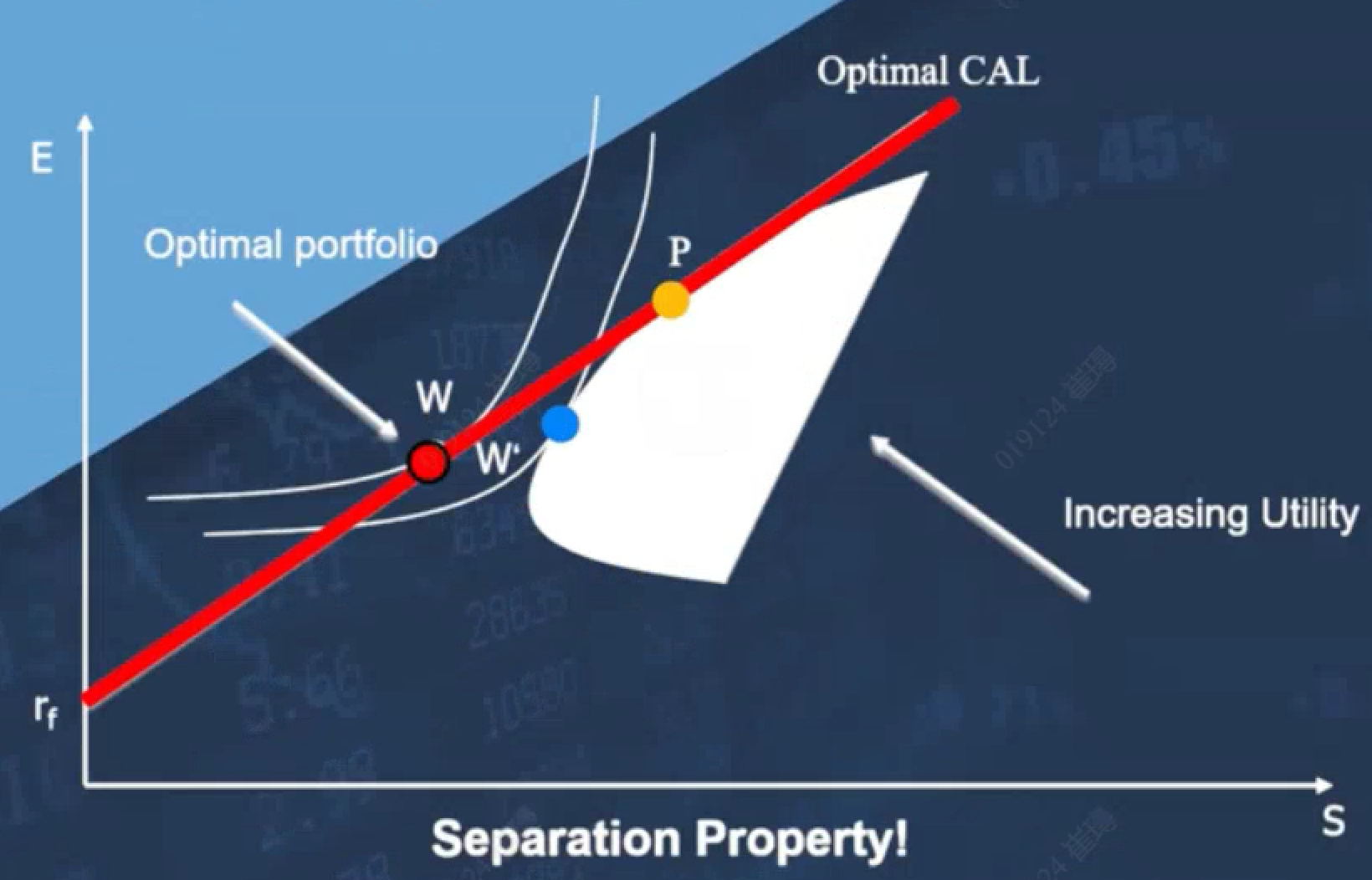
三、三步法 资产配置 总结
3.1 分离定律
从第二节可以看出,资产配置任务可以分配出独立的两个任务:
- 1.先决定最佳风险组合 -- optimal risky portfolio,这是纯粹的一个数学问题。和投资者的偏好没有任何关系,计算一次就可以使用到所有的投资者身上。
- 2.根据资本市场线 - capital market line,再根据投资人的风险偏好 - ,去寻找最优资产组合 - optimal portfolio。风险承受高的,选取资本市场线的右上方;反之,选择左下方。
其实对于所有的投资经理,都是再用二次效用方程,和P 以及 rf 的连线,连起来求解。

3.2 结论
把多种资产进行组合,可以降低资产收益的方差,也就是降低风险。
资产之间的相关性越低,分散风险的效果越强
资产种类越多,分散风险的效果越强
四、风险分散理论 及其 含义
横轴是资产种类数目
纵轴是portfolio的收益率
深蓝色 1种资产
红色 2个资产
黄色 5个资产
亮蓝色 10个资产
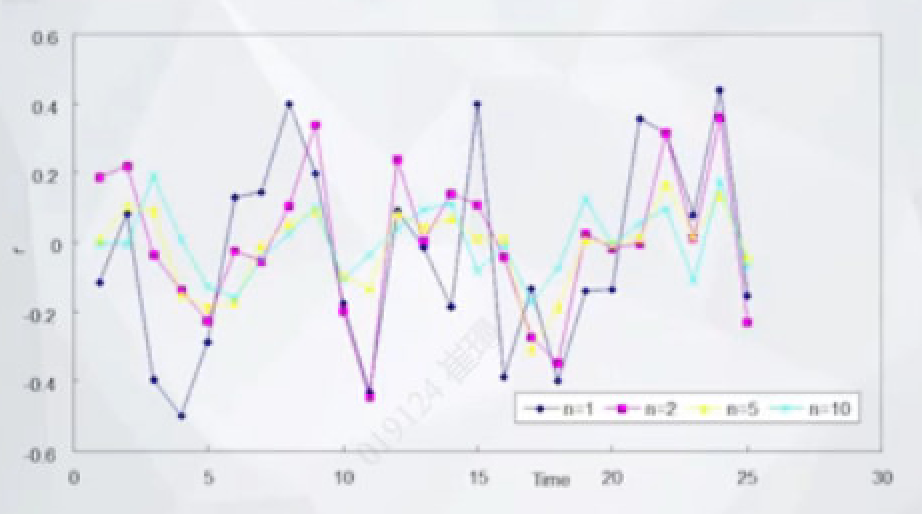
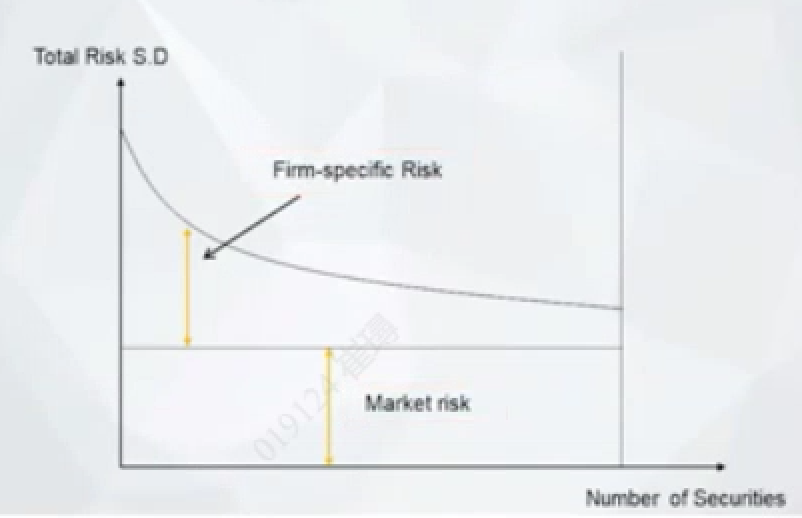
随着资产种类的增加,其波动的确在下降....但这个波动不能无限制的下降,不会归零
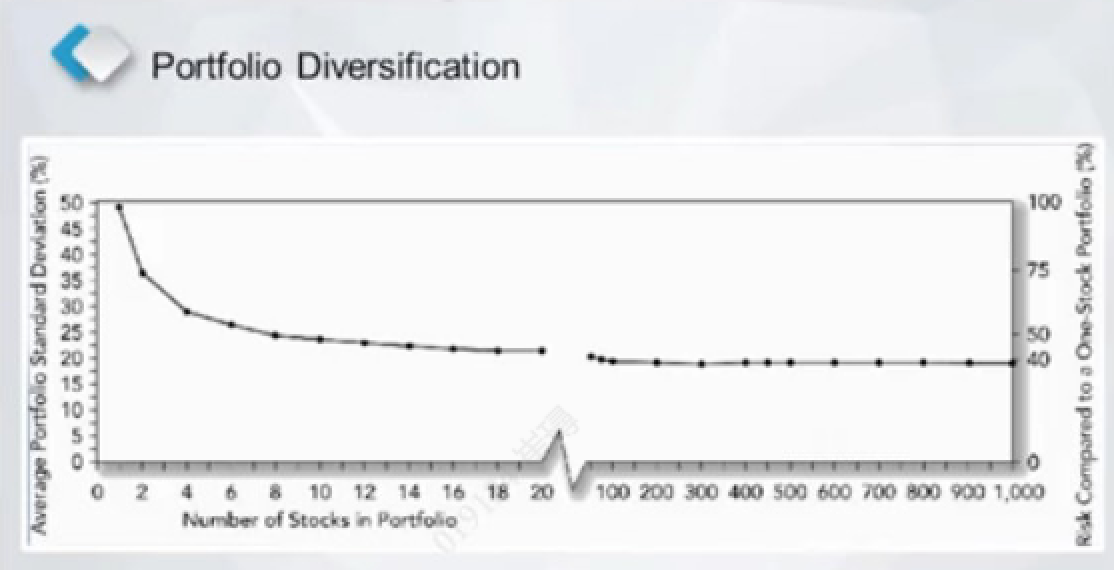
4.1 公司自有风险 vs 系统风险
我们把由方差代表的风险称作总风险,可以分为两个部分:
- 能被资产配置分散掉的风险,是公司自有的风险 - firm specific risk
- 理论上讲,可以被另一个具有相反风险暴露的公司,对冲掉。
- 自语风险无法被定价 not priced
- 不能被分散掉的风险,是市场风险/系统风险 - market risk/systematic risk
- 受宏观指标影响,货币政策,通货膨胀等等.无法被对冲。
- 市场风险可以被定价 priced;不是白白承担的,是有回报的。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号