图论4——探索网络流的足迹:Dinic算法
1. 网络流:定义与简析
1.1 网络流是什么?
网络流是一种“类比水流的解决问题方法,与线性规划密切相关”(语出百度百科)。
其实,在信息学竞赛中,简单的网络流并不需要太高深的数学知识。
首先我们需要知道一些名词是什么意思:
- 点(\(node\))。就是一个节点。点集通常用\(V\)表示。其中,有一个源点\(s\)和一个汇点\(t\),所有的流都从源点\(s\)出发,经过一些边之后到达汇点\(t\)。
- 边(\(edge\))。这个东西和大家在其他图论知识中所用到的差不多,用于连接两个点。边集通常用\(E\)表示。图\(G(V,E)\)表示由点集\(V\)和边集\(E\)组成的图\(G\)。在接下来讲到的有关网络流的问题中,边都是有向的。
- 容量(\(capacity\),简称\(cap\))。对于每一条边,我们都有一个容量,表示这条边最多能经过的流。
1.2 问题简述
显然,根据如上定义,到达汇点\(t\)的流是有限的。网络流问题(NetWork Flow Problem)就是如何合理安排一种方式,使得从源点\(s\)到汇点\(t\)的流最多。
感觉枯燥吗?其实我们可以这么感性的理解。
你的家里有\(10^{10^{10^{10}}}\)箱苹果,然后你要通过一些高速公路把他们运到你的亲戚家。由于某些限制,连接\(u\)和\(v\)的高速公路\((u,v)\)一天只能允许载有不超过\(cap(u,v)\)的卡车通过。显然,一天之内,能运送的苹果数量是有限的,因为这些高速路的限制只能让你运送其中的一些。那么如何安排这些苹果的运送方式,使得一天之内最后运到你亲戚家的苹果最多?
显然,即使你把所有的\(10^{10^{10^{10}}}\)箱苹果都运送给你的亲戚,但是最后绝大多数都会在高速路收费站被拦下来——超载(并且最后被工作人员吃掉)。最多能够送给亲戚的苹果数(即在最优方案下到达\(t\)的流)就称之为最大流。
2. 网络流:尝试与解决
2.1 贪心分析
A:这个问题不是可以贪心一遍然后\(O(n+m)\)就解决了吗?
B:怎么贪心?你做一遍试一下啊!
A:就是每一次都尽量多地往汇点送,如果下一条边不能再运送这么多的容量就分到其他条边不就好了吗?
B:(随手一个图)
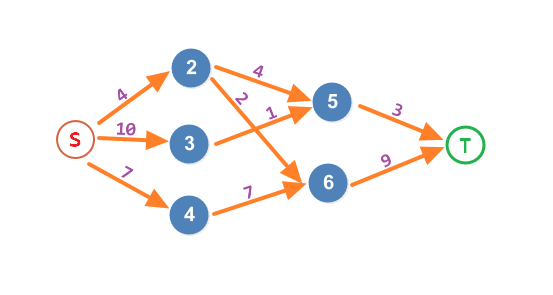 。
。
A:然后我开始详细讲我的贪心算法了。
\(\quad\)首先我们从\(s\to 2\to 5\to t\)运送\(3\)箱苹果,从\(s\to 2\to 6\to t\)运送\(1\)箱苹果;
\(\quad\)然后……\(s\to 3\to 5\to t\)就不行了……
\(\quad\)最后\(s\to 4\to 5\to t\)还有\(7\)箱。这样合计\(11\)箱。(强行掩饰)那你有更好地解法吗?
B:显然有。如果你没有这么贪心,从\(s\to 2\to 5\to t\)只运送\(2\)箱苹果,剩下两箱从\(s\to 2\to 6\to t\)走,这样\(s\to 3\to 5\to t\)还可以运一箱。最后\(s\to 4\to 5\to t\)还有\(7\)箱。合计\(2+2+1+7=12\)箱。
通过这段对话,我们发现,由于输入顺序未知,贪心很容易产生问题(尽管在这张图中你有一半的可能得到正确答案,而在数据量大的时候,不出错的概率很小)。所以我们考虑正确的解法。
2.2 朴素算法
在学习朴素算法之前,我们需要补充一个网络流中常用到的定理。
如果设\(f(u,v)\)为实际从这条边上走过的流量大小,则:
- 容量原则:\(f(u,v)\le cap(u,v)\).这个是显然的,你不可能实际流量比限制容量还大(否则你会因为超载被警察叔叔开罚单)。
- 反对称性:\(f(u,v)=-f(v,u)\).这个也是显然的,你送给亲戚\(10\)个苹果不就相当于你从亲戚那里拿到了\(-10\)个苹果吗?(尽管听上去总感觉好像不太正常)
- 流量守恒:当\(u\ne s,t\)时,如果规定边\((u,v)\)和\((v,u)\)都不存在时\(f(u,v)=f(v,u)=0\)的话,那么\(\displaystyle\sum^{v\in V}_ {v} f(u,v) =0\)。这个并不是那么好理解,简单来说,因为从\(s\)点流出的流最终都汇入\(t\),所以中间所有边都不会有剩下的流没有出去。只有\(s\)和\(t\)会“制造”和“接受”流量。(你不想让高速路的工作人员把你的苹果吃掉,所以一定选取刚好的苹果给亲戚;自然亲戚会全部收到,所以高速路的工作人员没有办法拦下你的苹果)。
有了这三条定理,我们就开始讲朴素算法。
我们首先给每一条边连上反向边。这条反向边的性质就像上面定理2“反对称性”中的反向边一样。
由于目前的网络流算法都基于增广路思想,我们还是要介绍一下增广路。
增广路思想
增广路定义:一条从源点到汇点的路径,使得路径上任意一条边的残量\(>0\)(注意是\(>\)而不是\(\ge\),这意味着这条边还可以分配流量),这条路径便称为增广路。
我们设\(g_{u,v}\)表示\((u,v)\)这条边上的残量,即剩余流量。
- 找到一条增广路,记这条路径上的边集为\(P\)。
- 记\(flow=\displaystyle\min_{(u,v)}^{(u,v)\in P} g_{u,v}\).
- 将这条路径上的每一条有向边\(u,v\)的残量\(g_{u,v}\)减去\(flow\),同时对于反向边\(v,u\)的残量加上\(flow\)。
- 重复上述过程,直到找不出增广路,此时我们就找到了最大流。
为什么反向边要加上\(flow\)呢?因为对于下面这个例子:
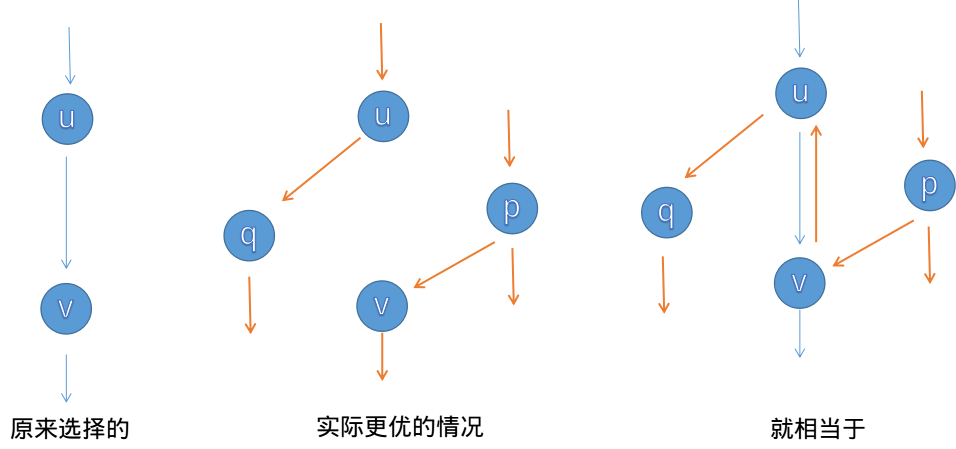
所以需要加上\(flow\)。
复杂度分析
这个复杂度是\(O(nm^2)\),而且往往不会少跑很多,所以只能用过\(n,m\le 300\)的数据。
Dinic算法
我们发现朴素算法有的时候会跑得特别特别的慢,因为增广路径查找得很不优秀。比如:

如果程序很不友好的在\((3,4)\)和\((4,3)\)中来回跑,那么显然复杂度会高到离谱。所以在Dinic中,我们引入分层图的概念。
分层图
对于每一个点,我们根据从源点\(s\)开始的bfs序,为每一个点分配一个深度\(dep_i\),然后通过不断dfs寻找增广路,每一次dfs当且仅当\(dep_v=dep_u+1\)是才从\(u\)到\(v\),这样上面的情况就避免了。
复杂度估计
那么Dinic的复杂度是多少呢?答案是\(O(n^2m)\)。事实上这只是最差情况下的估计,实际上远没有这么大,对于\(n,m\le 10^5\)的数据往往是可以轻松过的。
代码:
下面是代码。其中\(d\)数组即\(dep_i\),每次通过bfs构造层次图,然后dfs增广。
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int MAXN=100010;
const int INF=0x3f3f3f3f;
class Dinic
{
private:
struct edge
{
int from,to,cap,flow;
};
vector<edge>e;
vector<int>f[MAXN];
queue<int>q;
bool vis[MAXN];
int d[MAXN];
int cur[MAXN];
bool bfs()
{
memset(vis,0,sizeof(vis));
while(!q.empty())
q.pop();
q.push(s);d[s]=0;vis[s]=1;
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=0;i<f[x].size();i++)
{
edge &y=e[f[x][i]];
if(!vis[y.to]&&y.flow<y.cap)
{
vis[y.to]=1;
d[y.to]=d[x]+1;
q.push(y.to);
}
}
}
return vis[t];
}
int dfs(int x,int a)
{
if(x==t)
return a;
if(a==0)
return 0;
int flow=0,r;
for(int &i=cur[x];i<f[x].size();i++)
{
edge &y=e[f[x][i]];
if(d[x]+1==d[y.to]&&(r=dfs(y.to,min(a,y.cap-y.flow)))>0)
{
y.flow+=r;
e[f[x][i]^1].flow-=r;
flow+=r;
a-=r;
if(a==0)
break;
}
}
return flow;
}
public:
int n,m,s,t;
void adde(int u,int v,int cap)
{
e.push_back((edge){u,v,cap,0});
e.push_back((edge){v,u,0,0});
this->m=e.size();
f[u].push_back(m-2);
f[v].push_back(m-1);
}
int maxflow()
{
int res=0;
while(bfs())
{
memset(cur,0,sizeof(cur));
res+=dfs(s,INF);
}
return res;
}
};
如果需要使用这个模板,只需要输入\(n,s,t\),而\(m\)将根据加边次数计算。
这个模板的技巧在于,存反向边的时候利用了位运算\(xor\)的技巧:如果边的编号从\(0\)计数,那么相邻的边编号就是\(2x,2x+1\),在计算机中\(2x\ xor\ 1=2x+1\),而\((2x+1)\ xor\ 1=2x\)。这样可以很方便的读取反向边。



