图论3——图的存储与基本性质

本文作者frankchenfu，blogs网址http://www.cnblogs.com/frankchenfu/，转载请保留此文字。

在数学上，图是表示物件与物件之间联系的数学对象；而在计算机中，每个物件可以抽象成一个节点，而关系就是一条边。

这里主要介绍图的一些较关键的性质以及邻接矩阵、邻接表的应用。

1、有向图和无向图

图分为有向图和无向图。顾名思义，有向图就是每条边都具有方向，一条从$A$->$B$的有向边它可以让一个东西从$A$走到$B$，却不能沿同一条边从$B$走回$A$；反之，无向图就是不具有方向的，既可以从$A$到$B$，也可以沿同一条边从$B$到$A$。一条边可能有一个权值，叫边权。

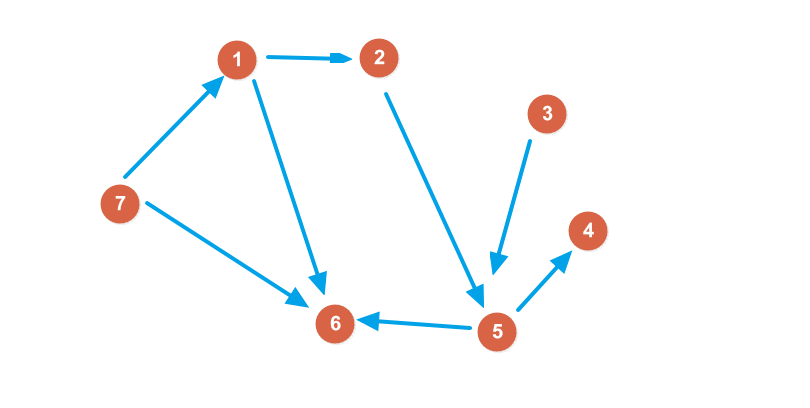
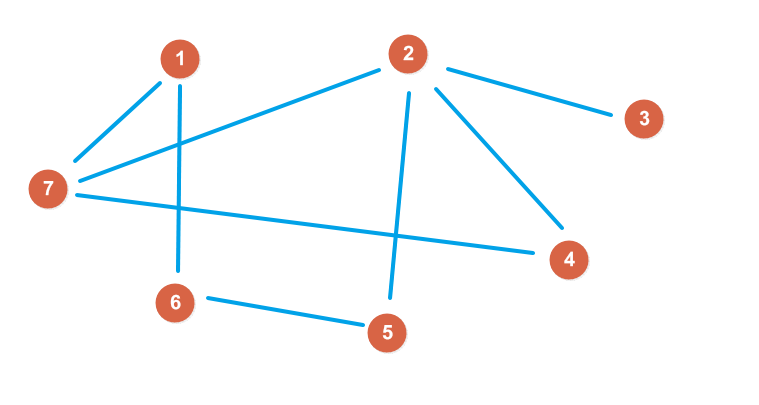
　　　　　　　　　　　有向图　　　　　　　　　　　　　　　　　　　　　　　　　　　　　无向图

注意到上面这一句话中，我强调了同一条边。这表明，一张图中可能会有重复的边，即起点和终点相同的边（在无向图中可能是起点终点位置调换的边），我们把这样的边成为重边。

如果一张图中，有$n$个结点，同时还有着$n-1$条边，那么这张图事实上是一颗树。

如果这张图中，从$A$一直沿着某些不重复的边走，然后能走回$A$，那么这张图中就存在着环。一张图中可能存在着很多个环，也可能一个都没有。例如，在上面的有向图中，不存在环，而在无向图中，结点$2,4,7$构成了一个环。

2、图的存储

限于篇幅，这里仅介绍最常用的邻接矩阵和邻接表。

2.1 邻接矩阵法

 我们可以构造一个矩阵，矩阵的第$i$行第$j$列（即$g_{i,j}$）表示结点$i$和结点$j$的关系，而没有连边的两个节点，我们就设置为“假想无穷大”。例如，上面的有向图可以表示为（inf即“假想无穷大”）：

这里为第$i$行第$j$列为1表示有连边。大家可以自行验证是否表示上述有向图。用代码表示就可以是 g[i][j]=1; .无向图也可以类似的表示，注意，因为边是无向的，所以一旦第$i$行第$j$列有连边，那么第$j$行第$i$列也一定是有连边的。用代码表示即为 g[i][j]=g[j][i]=1; 。那么邻接矩阵法就讲完了。可是，如果对于这样一个数据范围：

对于$100$%的数据满足$n \le 10^6 , m \le 10^6$，其中$n$表示节点数，$m$表示边数。

如果空间限制是标准的256MB或512MB，即使是1GB，存邻接矩阵也是不够的啊！邻接矩阵的二维数组的空间消耗是O($n^2$)的。注意到有很多无用的空间，也就是上面的inf，事实上比我们有用的空间还多（在浏览上面的表格时你有没有这么想呢？）。因为边的数量较小，于是我们考虑，能不能主要存边的信息，而尽量不存点呢？于是我们的邻接表就出来了。

2.2 邻接表法

邻接表的思想就是存边的信息，而不是点的信息。我们给每一条边一个编号。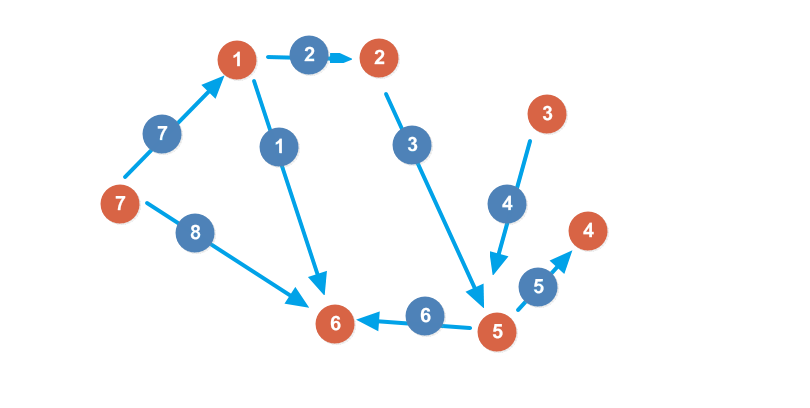

仍然对于上面的有向图，我们邻接表里存的内容可以这么表示：（其中冒号前的数字表示表示这一条边的编号）

邻接表存的就是这么一个东西。它首先每个节点都有存一个“从这条边出发的第一条边”，然后每一条边除了保存自身的信息（包括到哪里去，权值等）以外，还有指向下一条边的编号。这让我们想起了什么？对，链表！它每个节点内存的内容就很像链表，然后下一条边指向0就表示结束了，这个节点的边就遍历忘了。这样也是可以存储一个图的。这种方法的优点就是空间复杂度上的优势，它的空间复杂度（如果不考虑每个节点存的“第一条边”的话）是O($m$)的。那么对于上面的数据范围就可以很轻松的解决了。其中fir数组存的是从$i$点连出的编号最大的边。

可是这种方法也有缺点，例如判断点之间是否联通，那么查找最坏情况下要O($m$)的复杂度，而邻接矩阵只需要O($1$)。

接下来给出两种存图方法的Cpp代码：

#include<cstdio>
#include<cstring>
//邻接矩阵
const int MAXN=3010;
int g[MAXN][MAXN];//graph
int n,m;

//在一般情况下，u和v分别表示边的起点和终点，w表示权值
void init()
{
    memset(g,0x7f,sizeof(g));//inf
    for(int i=1;i<=n;i++)
        g[i][i]=0;
}
void adde(int u,int v,int w)
{
    g[u][v]=w;//有向
    g[u][v]=g[v][u]=w;//无向
}

#include<cstdio>
#include<cstring>
//邻接表
const int MAXN=100010;
const int MAXM=200010;//注意，无向图空间双倍!

struct edge
{
    int to,w,nxt;
}e[MAXM];
int fir[MAXN];
int n,m,tot=0;

void adde(int u,int v,int w)
{
    e[++tot].to=v;e[tot].w=w;
    e[tot].nxt=fir[u];
    fir[u]=tot;
}

打一个广告，我自己的博客中还有使用邻接表储存的堆优化Dijkstra算法，有兴趣的同学可以浏览一下。限于水平，作者所写的难免有疏忽之处，望大家指正，Thanks！