算法设计与分析(实验班) Assignment 11
本文也可以在我的知乎上阅读。
Due: 1 pm on Friday, May 26
1 Search and Decision Problems
As discussed in class, NP is a class of decision problems, i.e., the answer is either “yes” or “no”. This choice is convenient and often also captures the difficulty of searching for a solution. In our class, we have shown the reduction from search to decision for some problems. Here, you will show the search-to-decision reduction for two more examples.
(1)
3-SAT: A 3-SAT formula consists of \(m\) clauses, each of which is a disjunction of three literals (where a literal is one of \(n\) variables or its negation). We say a 3-SAT formula \(F\) is satisfiable if there is an assignment of the \(n\) variables such that \(F\) evaluates to true. The 3-SAT problem asks us to decide whether a given \(F\) is satisfiable.
Suppose you are given a black box for a function \(\sf{3SAT}\) that determines whether a given 3-SAT formula is satisfiable with timing cost \(T_{\sf{3SAT}}\). Design an algorithm that finds a satisfying assignment for \(F\) (assuming it is satisfiable) using \(O(n)\) calls to \(\sf{3SAT}\) and polynomially many other steps. Prove that your algorithm is correct and analyze its running time.
逐一赋值并检查即可。
设这 \(n\) 个变量为 \(X_1, X_2, \ldots, X_n\)。
首先,测试 \(X_1 = {\sf true}\) 时原问题是否有解。具体来说,是询问 \(F \land (X_1 \lor X_1 \lor X_1)\) 是否有解。如果有,则令 \(X_1 := 1, F := F \land (X_1 \lor X_1 \lor X_1)\),求 \(X_2\) 的值。否则,若没有解,则令 \(X_1 = 0\),\(F := F\land (\overline{X_1} \lor \overline{X_1}\lor \overline{X_1})\),求 \(X_2\) 的值。以此类推即可。
(2)
3-Coloring: We say an undirected graph is 3-colorable if there is an assignment of the colors \(\{r, g, b\}\) to the vertices (a coloring) such that no two adjacent vertices have the same color. The 3-Coloring problem asks us to decide whether a given graph is 3-colorable.
Suppose you are given a black box for a function \(\sf 3Color\) that determines whether a given graph is 3-colorable with timing cost \(T_{\sf 3Color}\). Design an algorithm that finds a coloring of a given graph using \(O(n)\) calls to \(\sf 3Color\) and polynomially many other steps, where \(n\) is the number of vertices in the input graph. Prove that your algorithm is correct and analyze its running time.
逐一赋值并检查即可。
具体来说,设点的颜色为 \(X_1, X_2, \ldots, X_n\)。不妨设 \(X_1, X_2\) 有连边,设 \(X_1 = r, X_2 = g\)。
-
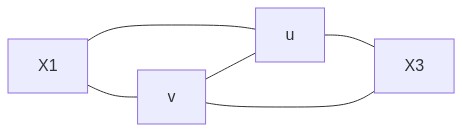
首先,测试 \(X_3 = r\) 时原问题是否有解。具体来说,是在图 \(G\) 增加点 \(u, v\) 与边 \((X_1, u), (X_1, v), (u, v), (u, X_3), (v, X_3)\),得到图 \(G'\)。很明显,这与令 \(X_3 = X_1\) 是等价的。如果有解,则令 \(G := G'\),继续求 \(X_4\)。
graph LR X1 --- u X1 --- v v --- u v --- X3 u --- X3 -
否则,测试 \(X_3 = g\) 时原问题是否有解,方法与上面类似。
-
若还是无解,则有 \(X_3 = b\),对原图 \(G\) 添加这些边 \((X_1, X_3), (X_2, X_3)\),得到 \(G'\)。这与添加约束 \(X_3 \ne X_1, X_3 \ne X_2\) 等价(相当于令 \(X_3 = b\))。之后,令 \(G := G'\),继续求 \(X_4\) 即可。
graph LR X1 --- X3 X2 --- X3
显然,上面的过程至多调用了 \(2(n-2)\) 次 \(\sf 3Color\),对原图添加至多 \(2(n-2)\) 个点,\(5(n-2)\) 条边,符合要求。
2 3-Dimensional Matching
In our class, we introduced how to solve the bipartite matching problem in polynomial time. In particular, the perfect bipartite matching problem can be written in the following way: Suppose we are given two disjoint sets \(A\) and \(B\), each of size \(n\), and a set \(P\) of pairs drawn from \(A × B\). The goal is to determine whether there exists a set of \(n\) pairs in \(P\) such that each element in \(A ∪ B\) is contained in exactly one of these pairs.
As a generalization, consider the following \(3\)-dimensional matching problem: Suppose we are given three disjoint sets \(A\), \(B\), and \(C\), each of size \(n\), and a set \(T\) of triples drawn from \(A × B × C\). The goal is to determine whether there exists a set of \(n\) triples in \(T\) such that each element in \(A ∪ B ∪ C\) is contained in exactly one of these triples.
(1)
Prove that 3-dimensional-matching \(≤_P\) Set-Cover. This implies that 3-dimensional-matching \(∈\) NP.
这是显然的。下面叙述如何利用集合覆盖问题求解一个3维完美匹配问题。
首先,若 \(\bigcup T \ne A\cup B \cup C\),则显然没有3维完美匹配。
直接对 \(T\) 求解覆盖集合问题,若 \(A\cup B\cup C\) 能被 \(n\) 个集合 \(X_1, X_2, \ldots, X_n\) 覆盖,则这些集合 \(X_1, X_2, \ldots, X_n\) 显然是一个3维完美匹配。
否则,若 \(A\cup B\cup C\) 不能被 \(n\) 个集合 \(X_1, X_2, \ldots, X_n\) 覆盖,则 \(T\) 显然不存在3维完美匹配。
(2)
Prove that 3-SAT \(≤_P\) 3-dimensional-matching. Together with (1), this implies that the 3-dimensional-matching problem is NP-complete.
本部分大量参考了CMSC 451: More NP-completeness Results,图也都截自此。
考虑如何将 3-SAT 问题化归为3维覆盖问题:
-
对每个 3-SAT 问题里的变量 \(X_i\),建立一个构件(gadget),如图。

具体来说,创建一个共有 \(2k\) 个点的“核” \(A_i = \{a_{i,1}, \ldots, a_{i,2k}\}\) 以及一个共有 \(2k\) 个点的“尖端” \(B_i = \{b_{i,1},\ldots,b_{i,2k}\}\)。
最后,构造 \(2k\) 个三元组 \(t_{ij} = (a_{i,j}, a_{i,j+1}, b_{i,j})\)。
(本构造中直接令 \(k =\) 3-SAT 问题中分句的数量 \(m\))
这一步共构造了 \(4nk\) 个点,\(2nk\) 个集合。
这个构件有什么意义?
每一个这样的构件在3维完美匹配中,“核”的点是匹配奇数尖端 \(b_{i,1}, b_{i,3}, \ldots\) 还是匹配偶数尖端 \(b_{i,2},b_{i,4},\ldots\) 分别代表 3-SAT 问题中 \(X_i\) 是取真还是取假(如图)
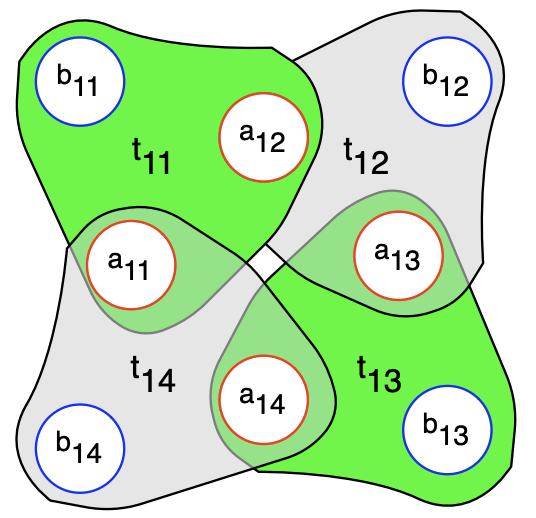
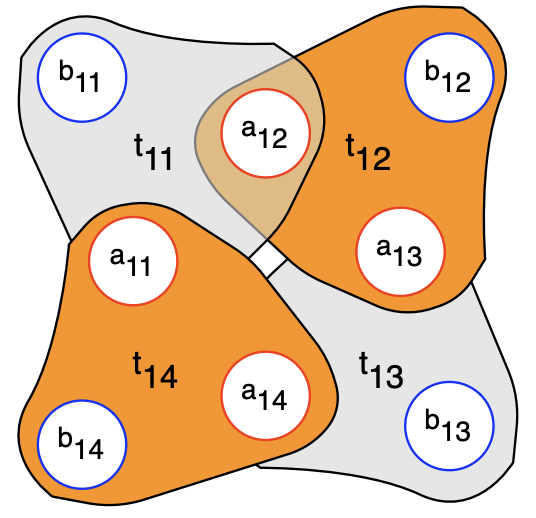
(很明显,如果所有“核”的点都有匹配,那么肯定要么全部匹配奇数尖端,要么匹配偶数尖端)
我们规定,匹配奇数尖端(空出偶数尖端)代表 \(X_i = {\sf true}\)(图1),匹配偶数尖端(空出奇数尖端)代表 \(X_i = {\sf false}\)(图2)。
-
对每个 3-SAT 问题里的分句(clause) \(C_i\),创建两个点 \(c_i, c_i'\),并且对所有在这个分句里的变量 \(X_j\),如果是以肯定形式 \(X_j\) 出现的,那么构造集合 \(\{c_i, c_i', b_{j,2i}\}\)。否则,如果是以肯定形式 \(\bar{X_j}\) 出现的,则构造集合 \(\{c_1, c_1', b_{j,2i-1}\}\)
例如,假设有 \(C_1 = X_1 \lor \overline{X_3} \lor \overline{X_5}\),先创建两个点 \(c_1, c_1'\),并构造三元集合 \(\{c_1, c_1', b_{1,2}\}, \{c_1, c_1', b_{3,1}\}, \{c_1, c_1', b_{5,1}\}\)。(如图)
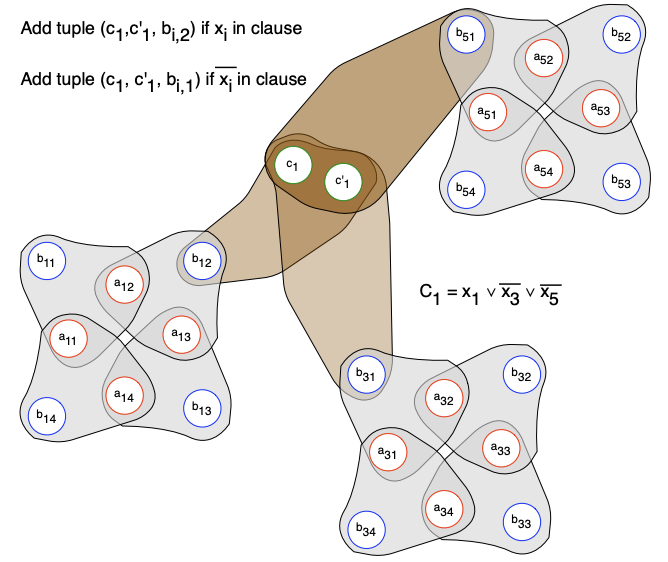
这样,\(\{c_1, c_1'\}\) 匹配哪个构件的点 \(b_{j,*}\) 就代表对应变量 \(X_j\) 的赋值满足 3-SAT 中分句的要求。
这一步共构造了 \(2m\) 个点,\(3m\) 个集合。
-
还有一个细节:
我们注意到,有很多尖端(具体来说是 \(nk - m\) 个)是不会被匹配的。为了让匹配成为完美匹配,需要对每个尖端 \(b\) 构造“清理小装置” \(\{q_i, q_i', b\}\),其中 \(i = 1, 2,\ldots, nk-m\)。
这一步共构造了 \(2(nk-m)\) 个点,\(k(nk-m)\) 个集合。
这样,我们把 3-SAT 问题在多项式时间内化归为了多项式规模的 3维完美匹配问题(3-SAT 问题有解 \(\iff\) 3维完美匹配问题有解)。\(\blacksquare\)
3 Restricted Monotone Satisfiability
Consider an instance of the Satisfiability problem, specified by clauses \(C_1, . . . , C_k\) over a set of Boolean variables \(x_1 , . . . , x_n\) . We say that the instance is monotone if each literal is a non-negated variable (i.e., \(x_i\) can appear as a literal but \(¬x_i\) cannot). Monotone instances are always satisfiable since we can simply set each variable to \(1\).
For example, suppose we have the three clauses
\[(x_1 ∨ x_2), (x_1 ∨ x_3),(x_2 ∨ x_3) \]This is monotone, and indeed the assignment that sets all three variables to \(1\) satisfies all the clauses. But we can observe that this is not the only satisfying assignment; we could also have set \(x_1\) and \(x_2\) to \(1\), and \(x_3\) to \(0\). Indeed, for any monotone instance, it is natural to ask how few variables we need to set to \(1\) in order to satisfy it.
Given a monotone instance of Satisfiability, together with a number \(k\), the problem of Restricted Monotone Satisfiability asks: is there a satisfying assignment for the instance in which at most \(k\) variables are set to \(1\)? Prove this problem is NP-complete.
首先,证明它是 NP 的:考虑将该问题化归为集合覆盖问题。
对将每一个变量 \(x_i\),构造它所对应的集合 \(X_i = \{C_j \mid x_i 出现在子句 C_j 中\}\)。\(x_i\) 为真相当于满足了 \(X_i\) 中所有子句的约束(“覆盖”了 \(X_i\) 中的所有子句 \(C_j\))。
这样,原问题可以看作在集合 \(C\) 上的一个集合覆盖问题:
给定全集 \(C = \{C_1, \ldots, C_k\}\) 与它的子集构成的集合 \(X = \{X_1, \ldots, X_n\}\),求是否存在一个大小为 \(k\) 的集合覆盖。
若此集合覆盖问题有解,则它的解对应原问题的一个解。若此集合覆盖问题无解,则原问题也无解。
我们可以用同样的方法把集合覆盖问题化归为此问题,因而它是 NP-Complete的。\(\blacksquare\)
4 Do some Calculus!
For functions \(g_1,...,g_l\), we define the function \(\max(g_1,...,g_l)\) via
\[[\max(g_1,...,g_l)](x) = \max(g_1(x),...,g_l(x)) \]Consider the following problem. You are given \(n\) piecewise linear, continuous functions \(f_1 , . . . , f_n\) defined over the interval \([0, t]\) for some integer \(t\). You are also given an integer \(B\). You want to decide: do there exist \(k\) of the functions \(f_{i_1},...,f_{i_k}\) so that
\[\int^t_0 [\max(f_{i_1},...,f_{i_k})](x) \mathrm{d} x ≥ B \]Prove that this problem is NP-complete.
首先,证明它是 NP 的:它的解可以在多项式时间(\(O(n^2m^2)\),其中 \(m\) 是 \(f_i\) 的段数上界)内验证,所以它是 NP 的。
之后,证明它是 NP-Complete 的:利用第 3 题的结论,只需证明可以将 Restricted Monotone Satisfiability 问题化归为它。
构造函数
显然,
因此,原问题的解和 Restricted Monotone Satisfiability 问题的解是一一对应的。故原问题是 NP-Complete 问题。\(\blacksquare\)