Big Data Tech and Analytics --- Locality Sensitive Hashing

Motivation: finding "similar" sets in high-dimensional space

Defination:

• Distance Measures: Aim to find "near neighbors" in high-dimensional space
  • 　　We formally define “near neighbors” as points that are a “small distance” apart

• Jaccard distance/similarity
  The Jaccard Similarity/Distance of two sets is the size of their intersection / the size of their union:
  𝑠𝑖𝑚(𝐶₁, 𝐶₂ )=|𝐶₁ ∩ 𝐶₂ | / |𝐶₁ ∪ 𝐶₂ |
  𝑑(𝐶₁, 𝐶₂ )=1−|𝐶₁  ∩ 𝐶₂ | / |𝐶₁ ∪ 𝐶₂ |

1. Finding Similar Documents

Goal: Given a large number (N in the millions or billions) of text documents, find pairs that are “near duplicates”

Applications:

• Mirror websites, or approximate mirrors
  • Don’t want to show both in a search
• Similar news articles at many news sites
  • Cluster articles by “same story"

Problems:

• Many pieces of one document can appear out of order in another
• Too many documents to compare all pairs
• Documents are so large or so many that they cannot fit in main memory

Three Essential Steps to solve problems:

• Shingling: Convert documents to sets
• Minhashing: Convert large sets to short signatures, while preserving similarity
• Locality-sensitive hashing: Focus on pairs of signatures likely to be from similar documents (Candidate pairs!)

 

 1.1 Shingling

　　1.1.1 Definition

　　　　A k-shingle (or k-gram) for a document is a sequence of k tokens that appears in the doc.

　　　　Tokens can be characters, words or something else, depending on the application

　　　　Assume tokens = characters for examples

　　　　Example: k = 2; document D1 = abcab

　　　　Set of 2-shingles: S(D1)={ab, bc, ca}

　　1.1.2 Compressing Shingles

　　　　To compress long shingles, we can hash them

　　　　Represent a doc by the set of hash values of its k-shingles

　　　　Idea: Two documents could (rarely) appear to have singles in common, when in fact only the hash-values were shared
　　　　Example: k = 2; document D1 = abcab
　　　　Set of 2-shingles: S(D1)={ab, bc, ca}
　　　　Hash the shingles: h(D1)={1, 5, 7}

 

　　1.1.3 Similarity Metric for Shingles

　　　　Document D1 = set of k-shingles C1 = S(D1)

　　　　Equivalently, each document is a 0/1 vector in the space of k-shingles. E.g. C1 = [0, 1, 0, 0, 0,1, 0, 0, 1, 0...]

　　　　Each unique shingle is a dimension. Vectors are very sparse.

　　　　A natural similarity measure is the Jaccard similarity: 𝑠𝑖𝑚(𝐶₁, 𝐶₂ )=|𝐶₁ ∩ 𝐶₂ | / |𝐶₁ ∪ 𝐶₂ |

1.2 MinHashing

　　1.2.1 Motivation

　　　　Suppose we need to find near-duplicate documents among N=1 million documents

　　　　Naively, we’d have to compute pairwise Jaccard similarities for every pair of docs

　　　　i.e. 𝑁(𝑁−1)/2≈5∗10^11 comparisons

　　　　At 10^5 secs/day and 10^6 comparison/sec, it would take 5 days

　　　　For N=10 million, it takes more than a year…

　　1.2.2 Encoding Sets as Bit Vector AND From sets to Boolean Matrices

　　　　Many similarity problems can be formalized as finding subsets that have significant intersection

　　　　Encode sets using 0/1 vectors

　　　　One dimension per element in the universal set

　　　　Interpret set intersection as bitwise AND, and set union as bitwise OR

　　　　Example: 𝐶₁ =10111; 𝐶₂=10011

　　　　　　Size of intersection = 3; size of union = 4,

　　　　　　Jaccard similarity = 3/4

　　　　　　𝑑(𝐶₁, 𝐶₂ )= 1 – (Jaccard similarity) = 1/4

　　　　Boolean Matrices:

　　　　　　Rows = elements (shingles)

　　　　　　Columns = sets (documents)

　　　　　　1 in row e and column s if and only if e is a member of s

　　　　　　Column similarity is the Jaccard similarity of the corresponding sets (rows with value 1)

　　　　　　Each document is a column

　　　　　　Example:

　　　　　　

 

　　　　1.2.3 Finding Similar Columns

　　　　Challenges: too many long columns to compare

　　　　1.2.3.1 Approach: 

　　　　1) Signatures of columns: small summaries of columns
　　　　2) Examine pairs of signatures to find similar columns
　　　　Comparing all pairs may take too much time – Job for LSH
　　　　3) Optional: Check whether columns with similar signatures are really similar

　　　　1.2.3.2 Key Ideas for hashing columns (Signatures)

　　　　Key idea 1: “hash” each column C to a small signature h(C), such that:

　　　　　　1) h(C) is small enough that the signature fits in RAM

　　　　　　2) 𝑠𝑖𝑚(𝐶₁, 𝐶₂ ) is the same as the “similarity” of signatures ℎ(𝐶₁) and ℎ(𝐶₂)

　　　　Key idea 2: Hash documents into buckets, and expect that “most” pairs of near duplicate docs hash into the same bucket!

　　　　1.2.3.3 Goal for Min-Hashing:

　　　　　　Find a hash function h(·) such that:

　　　　　　If 𝑠𝑖𝑚(𝐶₁, 𝐶₂) is high, then with high prob. ℎ(𝐶₁ )=ℎ(𝐶₂)

　　　　　　If 𝑠𝑖𝑚(𝐶₁, 𝐶₂) is low, then with high prob. ℎ(𝐶₁ )≠ℎ(𝐶₂)

　　　　　　Clearly, the hash function depends on the similarity metric. Not all similarity metrics have a suitable hash function. For Jaccard similarity: Min-hashing

　　　　1.2.3.4 Solution:

　　　　　　Imagine the rows of the boolean matrix permuted under random permutation 𝜋

　　　　　　Define a “hash” function ℎ_𝜋 (𝐶) = the number of the first (in the permuted order 𝜋) row in which column C has a value 1: 　　ℎ_𝜋(𝐶) = min_𝜋𝜋(𝐶)

　　　　　　Use several (e.g., 100) independent hash functions to create a signature of a column

　　　　Example:

　　　　In the second permutation order, firstly we look at the third row "1" means the first row in the permuted order. Since we find "0" in the third row of third column, we continue to find "2" in the second permutation order, and it's also "0" in the second cloumn of third column. As for "3", there is also "0" in the forth row of column. Finally we find "4" as the result shown in the following figure.

　　　　In conclusion, the smallest number in the permutation 𝜋  with the number "1" in the same row in the input matrix should be the result

　　　　

 

　　　　1.2.3.5 Property:

　　　　Choose a random permutation 𝜋

　　　　Claim: Pr[ℎ_𝜋(𝐶₁))=ℎ_𝜋(𝐶₂)] = 𝑠𝑖𝑚(𝐶₁, 𝐶₂)

　　　　1.2.3.6 Proof:

　　　

 

 

　　　　

 

 　　　　1.2.3.7 Similarity for Signatures

　　　　The similarity of two signatures is the fraction of the hash functions in which they agree

　　　　Example:

　　　　

 

 

 

　　　　Pick K=100 random permutations of the rows
　　　　Think of sig(C) as a column vector
　　　　sig(C)[i] = according to the i-th permutation, the index of the first row that has a 1 in column C:
　　　　𝑠𝑖𝑔(𝐶)[𝑖]=min⁡(𝜋_i (𝐶))
　　　　Note: The sketch (signature) of document C is small -- ~100 bytes!
　　　　We achieved our goal! We “compressed” long bit vectors into short signatures

1.3 Locality Sensitive Hashing

 1.3.1 First CUT

　　Goal: Find documents with Jaccard similarity at least s 

　　General idea: Use a (hash) function f(x,y) that tells whether x and y is a candidate pair: a pair of elements whose similarity must be evaluated

　　For minhash matrices:

　　　　　　Hash columns of signature matrix to many buckets

　　　　　　Each pair of documents that hashes into the same bucket is a candidate pair (for further examination)

　　How to find Candidate pairs:　　

　　　　　　Pick a similarity threshold s (0 < s < 1)

　　　　　　Columns x and y of signature matrix M are a candidate pair if their signatures agree on at least fraction s of their rows:

　　　　　　𝑀(𝑖,x )=𝑀(𝑖,y) for at least fraction s values of 𝑖

　　　　　　We expect documents x and y to have the same similarity as is the similarity of their signatures

　　1.3.2 LSH solution

　　　　1.3.2.1

 

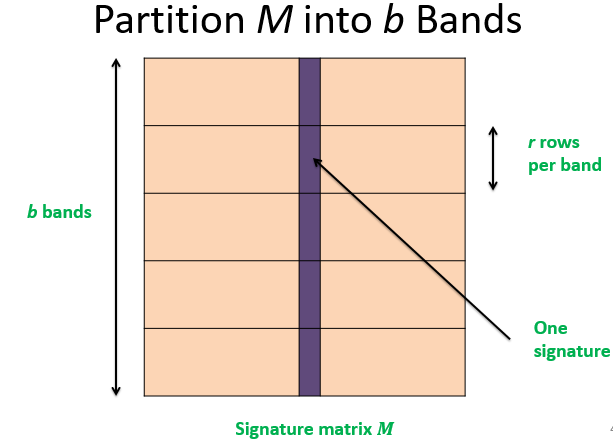
　　Divide matrix M into b bands of r rows

　　For each band, hash its portion of each column to a hash table with k buckets

　　　　Make k as large as possible

　　　　Assuming two vectors hash to the same bucket if and only if they are identical

　　Candidate column pairs are those that hash to the same bucket for ≥1 band

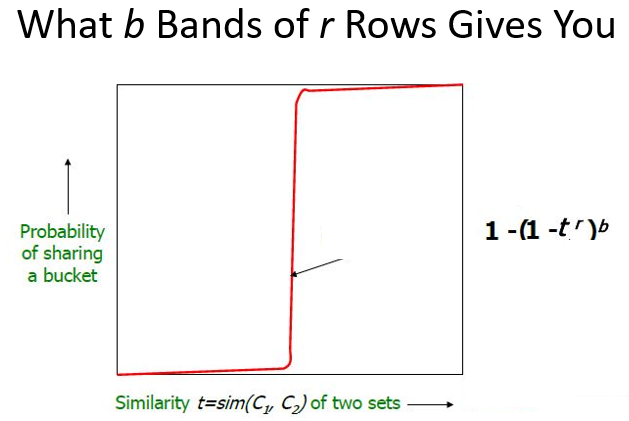
　　Tune b and r to catch most similar pairs, but few non-similar pairs

 

　　1.3.2.2 Assumption:

　　　　There are enough buckets that columns are unlikely to hash to the same bucket unless they are identical in a particular band
　　　　Hereafter, we assume that “same bucket” means “identical in that band”

　　　　Assumption needed only to simplify analysis, not for correctness of algorithm

　　1.3.2.3 Tradeoff to balance false positive and false negative

　　What influence:

　　　　the number of minhashes (rows of M)

　　　　the number of bands b

　　　　the number of rows r per band

　　Probability of true positive: