<<背包问题---01背包(原理,伪代码,编程实现)>>中已谈过01背包，这里再重写一下01背包的动态规划状态及状态方程：
设背包容量为V，一共N件物品，每件物品体积为C[i]，每件物品的价值为W[i]
1） 子问题定义：F[i][j]表示前i件物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值。
2） 根据第i件物品放或不放进行决策
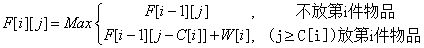(1-1)
最优方案总数这里指物品总价值最大的方案数。
我们设G[i][j]代表F[i][j]的方案总数，那么最总结果应该是G[N][V]。我们初始化G[][]为1，因为对每个F[i][j]至少应该有一种方案，即前i件物品中选取若干件物品放入剩余空间为j的背包使其价值最大的方案数至少为1，因为F[i][j]一定存在。
下面开始分析怎么求G[i][j]。对于01背包来说：
如果F[i][j]=F[i-1][j]且F[i][j]!=F[i-1][j-C[i]]+W[i]说明在状态[i][j]时只有前i-1件物品的放入才会使价值最大，所以第i件物品不放入，那么到状态[i][j]的方案数应该等于[i-1][j]状态的方案数即G[i][j]=G[i-1][j]；
如果F[i][j]=F[i-1][j-C[i]]+W[i] 且F[i][j]!=F[i-1][j]说明在状态[i][j]时只有第i件物品的加入才会使总价值最大，那么方案数应该等于[i-1][j-C[i]]的方案数，即G[i][j]=G[i-1][j-C[i]]；
如果F[i][j]=F[i-1][j-C[i]]+W[i] 且F[i][j]=F[i-1][j]则说明即可以通过状态[i-1][j]在不加入第i件物品情况下到达状态[i][j]，又可以通过状态[i-1][j-C[i]]在加入第i件物品的情况下到达状态[i][j]，并且这两种情况都使得价值最大且这两种情况是互斥的，所以方案总数为G[i][j]=G[i-1][j-C[i]]+ G[i-1][j]。
经过上面的分析，得出下述伪代码：
- F[0][] ← 0
- F[][0] ← 0
- G[][ ] ← 1
- for i ← 1 to N
- do for j ← 1 to V
- F[i][j] ← F[i-1][j]
- G[i][j] ← G[i-1][j]
- if (j >= C[i])
- if (F[i][j] < F[i-1][j-C[i]]+W[i])
- then F[i][j] ← F[i-1][j-C[i]]+W[i]
- G[i][j] ← G[i-1][j-C[i]]
- else if (F[i][j] = F[i-1][j-C[i]]+W[i])
- then G[i][j] ← G[i-1][j]+G[i-1][j-C[i]]
- return F[N][V] and G[N][V]
上述方法在保存状态F[][]及G[][]时需要O(NV)的空间复杂度，下面我们对空间复制度进行优化。
压缩空间复杂度为O(V)
F[i][j]与G[i][j]只分别与F[i-1][]和G[i-1][]的状态有关，所以我们可以用两个一维数组F[]和G[]来替换二维数组F[][]和G[][]。具体思想请看博文
<<背包问题——“01背包”详解及实现（包含背包中具体物品的求解）>>
下面直接给出伪代码：
- F[] ← 0
- G[] ← 1
- for i ← 1 to N
- do for j ← V to C[i]
- if (F[j] < F[j-C[i]]+W[i])
- then F[j] ← F[j-C[i]]+W[i]
- G[j] ← G[j-C[i]]
- else if (F[j] = F[j-C[i]]+W[i])
- then G[j] ← G[j]+G[j-C[i]]
- return F[V] and G[V]
下面对数据表给出详细代码：
| 物品号i | 1 | 2 | 3 | 4 | 5 |
| 体积C | 3 | 2 | 5 | 4 | 5 |
| 价值W | 5 | 5 | 10 | 10 | 10 |
#include<iostream>
using namespace std;
#define Size 1111
int dp[Size];
int Path[Size][Size];
int OptimalTable[Size];
int Max(int x,int y)
{
return x>y?x:y;
}
int Package01_Compress(int Weight[], int Value[], int goodsN, int maxWeight){
int i,j;
/*======初始化======*/
memset(dp,0,sizeof(dp));
memset(Path,0,sizeof(Path));
// memset(OptimalTable,1,sizeof(OptimalTable)); 这样初始化会出错
/*
因为memset是以字节为单位就是对array指向的内存的4个字节进行赋值，
每个都用ASCII为1的字符去填充，转为二进制后，1就是00000001,占一个字节。
一个INT元素是4字节，合一起就是00000001000000010000000100000001，
就等于16843009，就完成了对一个INT元素的赋值了。
所以用memset对非字符型数组赋初值是不可取的！
*/
for(int kt=0;kt<=maxWeight;kt++)
OptimalTable[kt]=1;
/*======初始化======*/
for(i=1;i<=goodsN;i++) //即怎么都有一种
for(j=maxWeight;j>=Weight[i];j--){
if(dp[j]<(dp[j-Weight[i]]+Value[i])){//说明选第i最优
dp[j] = dp[j-Weight[i]]+Value[i];
OptimalTable[j]=OptimalTable[j-Weight[i]];//方案数和[j-Weight[i]]一样
}
else if(dp[j]==(dp[j-Weight[i]]+Value[i])){
OptimalTable[j] = OptimalTable[j-Weight[i]]+OptimalTable[j];
}
//else dp[j]>dp[j-Weight[i]]+Value[i]--->
// 说明第i个不选 在weight=j这种情况下OptimalTable[j] =OptimalTable[j]
}
return dp[maxWeight];
}
int main()
{
int va[Size],vm[Size];
int t,n,m;
int i;
cin>>t; //t组测试数据
while(t--)
{
cin>>n>>m; //n为个数,m为最大载重量
for(i=1;i<=n;i++)
cin>>va[i];
for(i=1;i<=n;i++)
cin>>vm[i];
int myWhats=Package01_Compress(vm,va, n, m);
cout<<myWhats<<endl;
cout<<"-----一共有"<<OptimalTable[m]<<"组最优情况"<<endl;
}
return 0;
}版权声明：本文为博主原创文章，未经博主允许不得转载。
