线段树合并分裂学习笔记
线段树合并分裂学习笔记
思想
你想想你写一颗普通线段树是怎么写的,是不是把子区间的信息合并到父区间?
线段树合并大概就是这个想法,在树上每一个节点维护一颗权值线段树,把两棵线段树的信息合并到一个线段树上
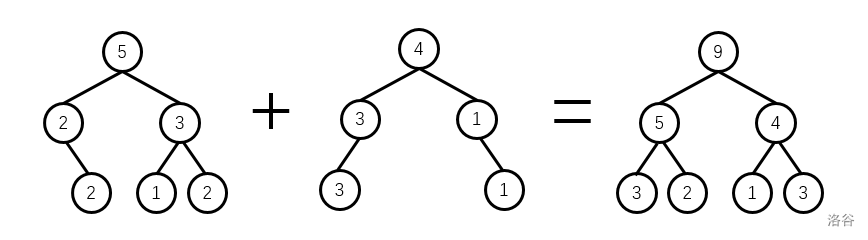
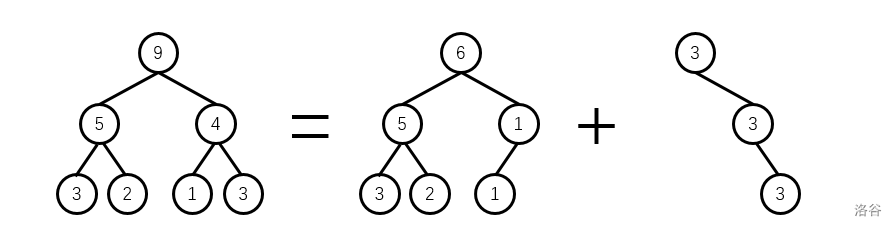
线段树分裂呢,就是把一棵权值线段树根据排名或值来割裂成两棵权值线段树,思路和fhq_treap的分裂类似,如下图
当然,由于给每一个节点都开一颗静态线段树空间肯定不够,且节点上线段树可能都不一定满,所以我们愉快地投进动态开点线段树的怀抱中.
这两操作的一次的时间复杂度都是\(O(log_{2}n)\)的
例题
1.P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并
这是板子吗?
对于添加\((x,y)\)路径上的所有点,暴力肯定是不行的,这里有一个经典解法是树上差分,即在\(x\),\(y\)上\(+1\),\(lca(x,y)\)上\(-1\),\(fa[lca(x,y)]\)上\(-1\)(画画图就懂了)
然后我们要处理的问题就是信息如何从子节点传上父节点,就线段树合并完事了.
注意合并时若两棵树一棵为空,返回另一棵即可
#include<bits/stdc++.h>
using namespace std;
int const MAXN=1e5+10,MAXM=2e7;
int n,m,tot,tott,_,N;
int h[MAXN],vis[MAXN],siz[MAXN],hson[MAXN],top[MAXN],fa[MAXN],dep[MAXN],val[MAXM],lc[MAXM],rc[MAXM],root[MAXM],ans[MAXM],X[MAXN],Y[MAXN],Z[MAXN],ansn[MAXN];
struct edge{
int to,next;
}e[MAXN<<1];
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}
return f*x;
}
inline void add(int u,int v){
e[++tot].to=v,e[tot].next=h[u],h[u]=tot;
}
void dfs1(int x,int dad){
siz[x]=1;fa[x]=dad;
int maxn=-1;
for(int i=h[x],to;i;i=e[i].next){
to=e[i].to;
if(to==dad)continue;
dep[to]=dep[x]+1;
dfs1(to,x);
siz[x]+=siz[to];
if(siz[to]>maxn)maxn=siz[to],hson[x]=to;
}
return;
}
void dfs2(int x,int topf){
top[x]=topf;
if(!hson[x])return;
dfs2(hson[x],topf);
for(int i=h[x],to;i;i=e[i].next){
to=e[i].to;
if(to==fa[x] || to==hson[x])continue;
dfs2(to,to);
}
return;
}
inline int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
if(dep[x]<dep[y])return x;
else return y;
}
void change(int &x,int l,int r,int p,int a){
if(!x)x=++tott;
if(l==r){val[x]+=a;if(val[x]>0)ans[x]=p;return;}
int mid=(l+r)>>1;
if(p<=mid)change(lc[x],l,mid,p,a);
if(p>mid)change(rc[x],mid+1,r,p,a);
if(val[lc[x]]>=val[rc[x]]){
val[x]=val[lc[x]];
ans[x]=ans[lc[x]];
if(!val[x])ans[x]=0;
}else{
val[x]=val[rc[x]];
ans[x]=ans[rc[x]];
if(!val[x])ans[x]=0;
}
}
int merge(int x,int y,int l,int r){
if(!x)return y;if(!y)return x;
if(l==r){val[x]+=val[y];if(val[x]>0)ans[x]=l;return x;}
int mid=(l+r)>>1;
lc[x]=merge(lc[x],lc[y],l,mid);
rc[x]=merge(rc[x],rc[y],mid+1,r);
if(val[lc[x]]>=val[rc[x]]){
val[x]=val[lc[x]];
ans[x]=ans[lc[x]];
if(!val[x])ans[x]=0;
}else{
val[x]=val[rc[x]];
ans[x]=ans[rc[x]];
if(!val[x])ans[x]=0;
}
return x;
}
void DFS(int x){
//printf("DFS in %d :",x);
for(int i=h[x];i;i=e[i].next){
int to=e[i].to;
if(to==fa[x])continue;
DFS(to);
root[x]=merge(root[x],root[to],1,N);
}
ansn[x] = ans[root[x]];
return;
}
void test(int x,int l,int r){
printf("%d %d %d\n",l,r,val[x]);
if(l==r)return ;
int mid=(l+r)>>1;
if(lc[x])test(lc[x],l,mid);
if(rc[x])test(rc[x],mid+1,r);
return;
}
int main(){
//freopen("data.in","r",stdin);
//freopen("data.out","w",stdout);
n=read();m=read();
for(int i=1,a,b;i<=n-1;i++){
a=read(),b=read();
add(a,b);add(b,a);
}
dep[1]=1;
dfs1(1,1);dfs2(1,1);
for(int i=1;i<=m;i++){
X[i]=read(),Y[i]=read(),Z[i]=read();
N=max(N,Z[i]);
}
for(int i=1;i<=m;i++){
int x=X[i],y=Y[i],z=Z[i];
change(root[x],1,N,z,1);
change(root[y],1,N,z,1);
int F=lca(x,y);
change(root[F],1,N,z,-1);
if(fa[F]!=F)change(root[fa[F]],1,N,z,-1);
}
DFS(1);
for(int i=1;i<=n;i++){
printf("%d\n",ansn[i]);
}
return 0;
}
Emm……当然可以二分答案+01序列排序来解决
但是,我们可是线段树合并和分裂的学习笔记丫!
而且线段树合并和分裂的速度甩了上一种不知道多少,而且还可以在线
先在每一个位置上建一棵权值线段树,对于一段区间我们合并节点,并用标记来表示它是正序还是倒序,用set来维护现存所有区间的左端点.当要排序的区间跨过原本有序的区间时,按照位置分裂原区间再进行合并
复杂度\(O(nlog_{2}n)\)
#include<bits/stdc++.h>
using namespace std;
int const MAXN=1e5+10,MAXM=MAXN*70;
int n,m,tot,tott,_,q;
int val[MAXM],lc[MAXM],rc[MAXM];
int root[MAXN];
bool sta[MAXN];
set<int>S;
typedef set<int>::iterator Sit;
void insert(int &x,int l,int r,int p,int a){
if(!x)x=++tot;
if(l==r){val[x]+=a;return;}
int mid=(l+r)>>1;
if(p<=mid)insert(lc[x],l,mid,p,a);
else insert(rc[x],mid+1,r,p,a);
val[x]=val[lc[x]]+val[rc[x]];
}
void merge(int &x,int y){
if(!(x&&y)){x|=y;return;}
val[x]+=val[y];
merge(lc[x],lc[y]);
merge(rc[x],rc[y]);
}
void split(int x,int &y,int s,int op){
if(val[x]==s)return;
val[y=++tot]=val[x]-s;val[x]=s;
if(op==0){
if(val[lc[x]]>=s){split(lc[x],lc[y],s,op);rc[y]=rc[x];rc[x]=0;}
else split(rc[x],rc[y],s-val[lc[x]],op);
}else{
if(val[rc[x]]>=s){split(rc[x],rc[y],s,op);lc[y]=lc[x],lc[x]=0;}
else split(lc[x],lc[y],s-val[rc[x]],op);
}
}
int query(int x,int l,int r){
if(l==r)return l;
int mid=(l+r)>>1;
if(lc[x])return query(lc[x],l,mid);
else return query(rc[x],mid+1,r);
}
Sit find(int p){
Sit k=S.lower_bound(p);
if(*k==p)return k;
--k;split(root[*k],root[p],p-*k,sta[p]=sta[*k]);
return S.insert(p).first;
}
int main(){
scanf("%d%d",&n,&m);
S.insert(n+1);
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
//insert(root[i],1,n,x,1);
insert(root[i],1,n,x,1);
S.insert(i);
}
for(int i=1;i<=m;i++){
int op,l,r;scanf("%d%d%d",&op,&l,&r);
Sit nl=find(l),nr=find(r+1);
for(Sit j=++nl;j!=nr;++j)merge(root[l],root[*j]);
sta[l]=op;S.erase(nl,nr);
}
scanf("%d",&q);
find(q);find(q+1);
printf("%d\n",query(root[q],1,n));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号