树链剖分学习笔记（未完）

树链剖分是在维护静态树上关于链的问题的好工具，感性的认识，就是把树问题转换为序列问题合并

而其中分为两种，一种是长链剖分，一种是重链剖分。

其实有超多好博客，如chinHhh's

重链剖分就是把树剖分成很多条两种类型的链，一种叫重链，一种叫轻链

而重链由重边构成，即任意一个父节点与其子树大小最大的儿子节点的连边

如图(From chinhhh)

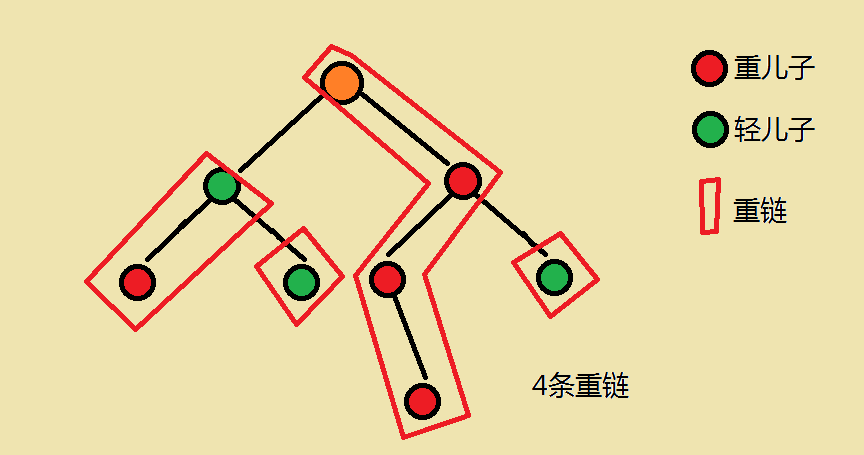
可以发现，任意一个节点在一条重链上（假设叶子节点自身也在一个重链），且任意一条重链不相交(由轻链连接)，所以我们只要维护重链就好了

然后最妙的是　通过先走重儿子再走其他儿子的dfs方法　，我们发现重链上的点在dfs序上连续了！！！这让我们可以用线段树之类的数据结构来维护重链，将问题看做链的合并

看一道板子：P3384 【模板】轻重链剖分

代码如下　时间复杂度\(O(nlog_2^2n)\)

#include<bits/stdc++.h>
using namespace std;
int const MAXN=1e6*4+10;
int N,M,R,P,tot=1,cnt;
int H[MAXN],val[MAXN],top[MAXN],dep[MAXN],id[MAXN],fa[MAXN],hson[MAXN],size[MAXN];
int w[MAXN];
bool vis[MAXN];
struct edge{
    int to,next;
}e[MAXN<<1];
struct node{
    int l,r,add,sum;
}p[MAXN<<2];
void add(int be,int to){
    e[++tot].to=be,e[tot].next=H[to],H[to]=tot;
    e[++tot].to=to,e[tot].next=H[be],H[be]=tot;
}
void dfs1(int x,int father,int depth){
    dep[x]=depth,fa[x]=father,size[x]=1;
    int maxn=0;
    for(int i=H[x];i;i=e[i].next){
        int to=e[i].to;if(to==father)continue;
        dfs1(to,x,depth+1);
        size[x]+=size[to];
        if(size[to]>maxn)hson[x]=to,maxn=size[to];
    }
}
void dfs2(int x,int topf){
    id[x]=++cnt,top[x]=topf,w[id[x]]=val[x];
    if(!hson[x])return;
    dfs2(hson[x],topf);
    for(int i=H[x];i;i=e[i].next){
        int to=e[i].to;
        if(to==fa[x] || to==hson[x])continue;
        dfs2(to,to);
    }
}
void build(int x,int l,int r){
    p[x].l=l,p[x].r=r;
    if(l==r){p[x].sum=w[l]%P;return;}
    int mid=(l+r)>>1;
    build(x<<1,l,mid);build(x<<1|1,mid+1,r);
    p[x].sum=(p[x<<1].sum+p[x<<1|1].sum)%P;
    return;
}
void pushdown(int x){
    if(p[x].add){
        p[x<<1].sum=(p[x<<1].sum+(p[x<<1].r-p[x<<1].l+1)*p[x].add)%P;
        p[x<<1|1].sum=(p[x<<1|1].sum+(p[x<<1|1].r-p[x<<1|1].l+1)*p[x].add)%P;
        p[x<<1].add=(p[x<<1].add+p[x].add)%P;
        p[x<<1|1].add=(p[x<<1|1].add+p[x].add)%P;
        p[x].add=0;
    }
}
void add(int x,int l,int r,int val){
    if(l<=p[x].l && r>=p[x].r){
        p[x].sum=(p[x].sum+val*(p[x].r-p[x].l+1))%P;
        p[x].add=(p[x].add+val)%P;
        return;
    }
    pushdown(x);
    int mid=(p[x].l+p[x].r)>>1;
    if(l<=mid)add(x<<1,l,r,val);
    if(r>mid)add(x<<1|1,l,r,val);
    p[x].sum=(p[x<<1].sum+p[x<<1|1].sum)%P;
}
int query(int x,int l,int r){
    if(l<=p[x].l && p[x].r<=r)return p[x].sum%P;
    pushdown(x);
    int mid=(p[x].l+p[x].r)>>1,val=0;
    if(l<=mid)val=(val+query(x<<1,l,r))%P;
    if(r>mid)val=(val+query(x<<1|1,l,r))%P;
    return val;
}
void add_way(int x,int y,int val){
    while(top[x]!=top[y]){
        if(dep[top[y]]>dep[top[x]])swap(x,y);
        add(1,id[top[x]],id[x],val);
        x=fa[top[x]];
    }
    add(1,min(id[x],id[y]),max(id[x],id[y]),val);
}
int query_way(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){
        if(dep[top[y]]>dep[top[x]])swap(x,y);
        ans=(ans+query(1,id[top[x]],id[x]))%P;
        x=fa[top[x]];
    }
    ans=(ans+query(1,min(id[x],id[y]),max(id[x],id[y])))%P;
    return ans;
}
void add_ctree(int x,int val){
    add(1,id[x],id[x]+size[x]-1,val);
}
int query_ctree(int x){
    return query(1,id[x],id[x]+size[x]-1);
}
int main(){
    scanf("%d%d%d%d",&N,&M,&R,&P);
    for(int i=1;i<=N;i++)scanf("%d",&val[i]);
    for(int i=1;i<=N-1;i++){
        int x,y;scanf("%d%d",&x,&y);add(x,y);
    }
    dfs1(R,R,1);
    dfs2(R,R);
    build(1,1,N);
    for(int i=1;i<=M;++i){
        int op,x,y,z;scanf("%d",&op);
        if(op==1){
            scanf("%d%d%d",&x,&y,&z);
            add_way(x,y,z);
        }else if(op==2){
            scanf("%d%d",&x,&y);
            printf("%d\n",query_way(x,y));
        }else if(op==3){
            scanf("%d%d",&x,&z);
            add_ctree(x,z);
        }else if(op==4){
            scanf("%d",&x);
            printf("%d\n",query_ctree(x));
        }
    }
    return 0;
}