电机速度曲线规划1：梯形速度曲线设计与实现

  电机驱动是很常见的应用，在很多系统中我们都会碰到需要改变电机的速度以实现相应的控制功能，这就涉及到电机速度曲线规划的问题。在这篇中我们就来简单讨论一下电机的梯形曲线规划的问题。

1、基本原理

  梯形速度曲线控制算法是工业控制领域应用最为广泛的加减速控制策略之一。所谓梯形速度曲线将整个运动过程分为匀加速、匀速和匀减速三个阶段，在变速过程中加速度保持不变。

  从变速过程中加速度保持不变这特点来说，其加减速过程其实是一个线性过程。我们可以采用一个线性函数来描述它。

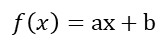
  这一线性函数，具体到我们的加减速过程中就是速度与时间的函数关系，函数结果就是我们某一时刻的速度，变量就是时间，斜率就是加速度，初始速度就是截距，具体如下：

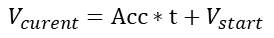
  这一函数表达的是连续的，但实际使用中我们需要离散化处理，我们必定以一定的时间间隔来处理速度的增加问题。这样实际的速度变化就不可能是连续的，而是阶梯状的，具体如下：

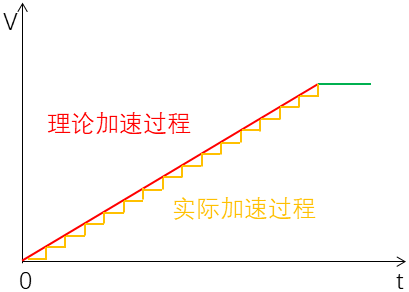
  为了速度的变化尽量平缓，我们需要尽可能地让时间间隔小一些，这其实是我们在考虑编写程序时需要处理的一个参数。

2、设计与实现

  我们已经简单描述了S型速度规划曲线的数学原理及应用表达式。接下来我们来考虑怎么实现它。

  考虑到在同一个驱动器中可能因为应用场景的需要存在多条的速度规划曲线。所以我们以基于对象的思路来考虑它，这样我们在更换不同的曲线就只需要更换不同的曲线实力就可以了。所以我们先来分析一下曲线对象的属性和操作。

  鉴于前面的分析，我们认为作为一个调速曲线对象至少要记录：开始调速时的初始速度、当前速度、目标速度、加速度、最大速度、最小速度、调速时间、调速时间跨度、曲线类型等，我们将这些记为对象的属性。据此我们可以定义电机速度曲线的对象类型为：

/* 定义电机速度曲线对象 */
typedef struct CurveObject {
  float startSpeed;    //开始调速时的初始速度
  float currentSpeed;   //当前速度
  float targetSpeed;    //目标速度
  float stepSpeed;     //加速度
  float speedMax;     //最大速度
  float speedMin;     //最小速度
  uint32_t aTimes;     //调速时间
  uint32_t maxTimes;    //调速跨度
  SpeedCurveType curveMode;  //曲线类型
}CurveObjectType;

 我们已经定义了一个速度曲线对象类型，接下来我们就来分析如何实现一个T型调速曲线。我们已经描述过，速度其实就是时间的函数，根据我们前面分析的速度时间的函数表达式，我们实现如下：

void (*pCalCurve[])(CurveObjectType *curve)={CalCurveNone,CalCurveTRAP,CalCurveSPTA};
 
/* 电机曲线加减速操作-------------------------------------------------------- */
void MotorVelocityCurve(CurveObjectType *curve)
{
  float temp=0;
  
  if(curve->targetSpeed>curve->speedMax)
  {
    curve->targetSpeed=curve->speedMax;
  }
  
  if(curve->targetSpeed<curve->speedMin)
  {
    curve->targetSpeed=curve->speedMin;
  }
 
  if((fabs(curve->currentSpeed-curve->startSpeed)<=curve->stepSpeed)&&(curve->maxTimes==0))
  {
    if(curve->startSpeed<curve->speedMin)
    {
      curve->startSpeed=curve->speedMin;
    }
    
    temp=fabs(curve->targetSpeed-curve->startSpeed);
    temp=temp/curve->stepSpeed;
    curve->maxTimes=(uint32_t)(temp)+1;
    curve->aTimes=0;
  }
  
  if(curve->aTimes<curve->maxTimes)
  {
    pCalCurve[curve->curveMode](curve);
    curve->aTimes++;
  }
  else
  {
    curve->currentSpeed=curve->targetSpeed;
    curve->maxTimes=0;
    curve->aTimes=0;
  }
}
 
/*梯形曲线速度计算*/
static void CalCurveTRAP(CurveObjectType *trap)
{
  float slope=0.0;
  
  slope=(trap->targetSpeed-trap->startSpeed)/trap->maxTimes;
    
  trap->currentSpeed=trap->startSpeed+slope*trap->aTimes;
 
  if(trap->currentSpeed>trap->speedMax)
  {
    trap->currentSpeed=trap->speedMax;
  }
  
  if(trap->currentSpeed<trap->speedMin)
  {
    trap->currentSpeed=trap->speedMin;
  }
}

  在这个实现中，我们出于更普遍的实用性考虑，将各种曲线的相同操作集成在一起，然后将它们差异的部分通过曲线类型属性以回调函数的方式集成。

3、应用与验证

  我们实现了T形电机速度规划曲线的基本设计与实现。接下来，我们就是用这一调速曲线来实现一个电机调速的实例。我们定义速度规划曲线时，是及与对象的思想来实现的，所以我们先声明一条曲线对象实例。

  CurveObjectType curve; //电机调速曲线

  在声明了这一曲线对象后，我们需要对其初始化赋值才能正确的使用。大多数的属性直接根据应用对象的要求给予初始值就可以了。需要注意的是曲线类型这一属性，这将决定使用什么样的速度规划曲线。该属性为SpeedCurveType枚举，该枚举定义如下：

/* 定义电机速度曲线类型枚举 */
typedef enum SpeedCurve {
  CURVE_NONE=0,  //直启
  CURVE_TRAP=1,  //梯形曲线
  CURVE_SPTA=2   //S型曲线
}SpeedCurveType;

  在这里我们需要将曲线类型初始化为T形速度规划曲线。具体操作如下：

  curve.curveMode=CURVE_TRAP;

  初始化完成之后就可以使用曲线对象来实现电机速度的调节了。使用也很简单，只要按一定的时间周期调用我们前面实现的MotorVelocityCurve函数就可以实现整个调速过程。具体如下：

  MotorVelocityCurve(&curve);

  在每次调速开始之前都需要设置取下的开始速度和目标速度，这样函数就会按照设定的起始速度和目标速度实现速度调整。

4、小结

  我们实现了梯形加减速曲线，并使用其实现了具体的应用。总体来说，当我们将参数设置的合适时，所起到的效果也是非常明显的。在我们的实际使用过程中，梯形曲线对大多数的应用基本都合适。不仅是在启动和停车过程，在运行过程中如果速度设定发生改变，也会调用曲线实现加减速过程。

  梯形速度曲线虽说实现简单，在一般的应用场合也能有不错的效果，但实际上还是有一定的问题。梯形速度曲线的加速度是一个常量，这就造成加速度的变化过程并不连续，在加减速阶段和匀速运动阶段的连接部分，加速度会发生突变，而这种突变可能会对控制目标产生冲击，而有些应用场合这种冲击是不允许的。

欢迎关注：