PID控制器改进笔记之四:改进PID控制器之设定值响应
前面我们发布了一系列PID控制器相关的文章,包括经典PID控制器以及参数自适应的PID控制器。这一系列PID控制器虽说实现了主要功能,也在实际使用中取得了良好效果,但还有很多的细节部分可以改进以提高性能和灵活性。所以在这篇中我们来讨论改进PID控制器以实现降低设定值阶跃带来的扰动。
1、提出问题
我们在使用PID控制器时,如果大幅度修改设定值有可能引入一个大的阶跃扰动。特别是对微分作用,这一扰动可能引起很大的振荡,这种情况我们通常称之为微分冲击。

为了应对因为微分作用对设定值变化造成的激烈响应,人们引入了微分先行的PID算法,这一算法是将基于偏差的微分修改为基于输入的微分。也就是说设定值的变化对微分不会有突变的影响,而只有作用在被控对象后微分才起作用,从而消除了设定值的变化带来的微分作用冲击。
然而有些时候,设定值的阶跃变化也会通过比例作用反映出来,这种冲击也会对系统造成振荡。当然我们也可以将其改为基于输入的比例,虽然也可以消除设定值的突变影响,但是比例和微分都是面向输入信号的对设定值的响应将会变得滞后,这也并非我们想要的。
所以我们希望能找到一种办法,既可响应设定值的变化,又不会造成大的冲击,这就是我们在此要考虑的问题。
2、分析设计
前面实际我们已经讨论了基于输入的比例和微分,这实际上改变了PID的调节方式,这里我们希望从另一个角度来考虑对设定值的响应问题。我们曾经讨论过步进式PID的控制方式就是一种比较好的处理办法。
所谓步进式PID算法,实际就是在设定值发生阶跃变化时,不直接对阶跃信号进行响应,而是在一定的时间内逐步改变设定值,直至使设定值达到目标值。这种逐步改变设定值的办法使得对象运行平稳。适用于高精度伺服系统的位置跟踪。
佷显然,这一方法并未改变PID控制器本身,而是对设定值做了前期处理。所以其结构框图与控制方程与其他的PID控制算法是一致的。
为了对设定值做必要处理,以使其不至快速变化,有多种方法。比较常用的是建立线性变化函数的办法。我们可以规定设定值从0-100%的变化时间为T,则可以确定设定值变化的斜率绝对值,或者说是步长。知道步长后,我们就可以根据步长来不断修改设定值,直到目标值。可用公式描述为:
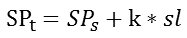
其中SPt为设定值目标值,SPs为设定值的起始值,sl为步长,k为步长的变化系数:

我们希望能够根据我们自己的需要使用步进或者不使用步进,所以我们需要在PID对象中添加一个属性来配置其是否使用。
1 /*定义PID对象类型*/ 2 typedef struct CLASSIC 3 { 4 float *pPV; //测量值指针 5 float *pSV; //设定值指针 6 float *pMV; //输出值指针 7 float *pKp; //比例系数指针 8 float *pKi; //积分系数指针 9 float *pKd; //微分系数指针 10 uint16_t *pMA; //手自动操作指针 11 12 float setpoint; //设定值 13 float lasterror; //前一拍偏差 14 float preerror; //前两拍偏差 15 float deadband; //死区 16 float result; //PID控制器计算结果 17 float output; //输出值0-100% 18 float maximum; //输出值上限 19 float minimum; //输出值下限 20 float errorabsmax; //偏差绝对值最大值 21 float errorabsmin; //偏差绝对值最小值 22 float alpha; //不完全微分系数 23 float deltadiff; //微分增量 24 float integralValue; //积分累计量 25 float gama; //微分先行滤波系数 26 float lastPv; //上一拍的过程测量值 27 float lastDeltaPv; //上一拍的过程测量值增量 28 29 ClassicPIDDRType direct; //正反作用 30 ClassicPIDSMType sm; //设定值平滑 31 32 }CLASSICPID;
3、软件实现
我们讨论的对设定值的响应方式,其实就是直接给定设定值或者采用步进式给定设定值。所谓步进式其实质是将设定值的突变修改为平缓的变化,这一处理方式在控制中有大量应用。处理设定值变化过程的流程如下所示:
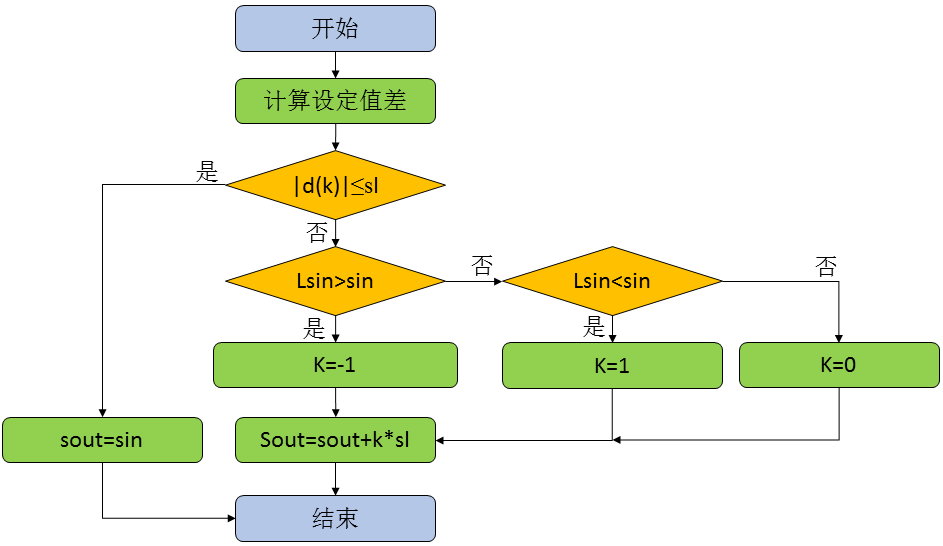
根据我们前面的描述和上面的流程图我们可以实现对PID控制器的修改。我们将对设定值处理的的部分单独置为函数,这样除了使用线性方式处理外我们也可以根据需要采取其他方式处理。
1 /*设定值平滑变化处理函数*/ 2 static void SmoothSetpoint(CLASSICPID *vPID) 3 { 4 float stepIn=(vPID->maximum-vPID->minimum)*0.1; 5 float kFactor=0.0; 6 7 if(fabs(vPID->setpoint-*vPID->pSV)<=stepIn) 8 { 9 vPID->setpoint=*vPID->pSV; 10 } 11 else 12 { 13 if(vPID->setpoint-*vPID->pSV>0) 14 { 15 kFactor=-1.0; 16 } 17 else if(vPID->setpoint-*vPID->pSV<0) 18 { 19 kFactor=1.0; 20 } 21 else 22 { 23 kFactor=0.0; 24 } 25 vPID->setpoint=vPID->setpoint+kFactor*stepIn; 26 } 27 } 28 29 /* 通用PID控制器,采用增量型算法,具有变积分,梯形积分和抗积分饱和功能,微分项采用不完全微分,一阶滤波,alpha值越大滤波作用越强 */ 30 void PIDRegulator(CLASSICPID *vPID) 31 { 32 float thisError; 33 float result; 34 float factor; 35 float increment; 36 float pError,dError,iError; 37 38 if(*vPID->pMA<1) //手动模式 39 { 40 vPID->output=*vPID->pMV; 41 //设置无扰动切换 42 vPID->result=(vPID->maximum-vPID->minimum)*vPID->output/100.0+-vPID->minimum; 43 *vPID->pSV=*vPID->pPV; 44 vPID->setpoint=*vPID->pSV; 45 } 46 else //自动模式 47 { 48 if(vPID->sm==SMOOTH_ENABLE) 49 { 50 SmoothSetpoint(vPID); 51 } 52 else 53 { 54 vPID->setpoint=*vPID->pSV; 55 } 56 57 thisError=vPID->setpoint-(*vPID->pPV); //得到偏差值 58 result=vPID->result; 59 if (fabs(thisError)>vPID->deadband) 60 { 61 pError=thisError-vPID->lasterror; 62 iError=(thisError+vPID->lasterror)/2.0; 63 dError=thisError-2*(vPID->lasterror)+vPID->preerror; 64 65 //变积分系数获取 66 factor=VariableIntegralCoefficient(thisError,vPID->errorabsmax,vPID->errorabsmin); 67 68 //计算微分项增量带不完全微分 69 vPID->deltadiff=(*vPID->pKd)*(1-vPID->alpha)*dError+vPID->alpha*vPID->deltadiff; 70 71 increment=(*vPID->pKp)*pError+(*vPID->pKi)*factor*iError+vPID->deltadiff; //增量计算 72 } 73 else 74 { 75 if((fabs(vPID->setpoint-vPID->minimum)<vPID->deadband)&&(fabs((*vPID->pPV)-vPID->minimum)<vPID->deadband)) 76 { 77 result=vPID->minimum; 78 } 79 increment=0.0; 80 } 81 82 //正反作用设定 83 if(vPID->direct==DIRECT) 84 { 85 result=result+increment; 86 } 87 else 88 { 89 result=result-increment; 90 } 91 92 /*对输出限值,避免超调和积分饱和问题*/ 93 if(result>=vPID->maximum) 94 { 95 result=vPID->maximum; 96 } 97 if(result<=vPID->minimum) 98 { 99 result=vPID->minimum; 100 } 101 102 vPID->preerror=vPID->lasterror; //存放偏差用于下次运算 103 vPID->lasterror=thisError; 104 vPID->result=result; 105 106 vPID->output=(vPID->result-vPID->minimum)/(vPID->maximum-vPID->minimum)*100.0; 107 *vPID->pMV=vPID->output; 108 } 109 }
4、总结
我们引入了让设定值不大范围突变的方式,而不需要改变PID控制器的控制方式。经测试效果能够满足我们的要求。在我们这里步长固定采用量程的十分之一,事实上我们可以将其作为初始化参数予以修改,甚至我们也可以采用一定条件下变步长的方式来满足更高的控制要求。
欢迎关注:

如果阅读这篇文章让您略有所得,还请点击下方的【好文要顶】按钮。
当然,如果您想及时了解我的博客更新,不妨点击下方的【关注我】按钮。
如果您希望更方便且及时的阅读相关文章,也可以扫描上方二维码关注我的微信公众号【木南创智】


 浙公网安备 33010602011771号
浙公网安备 33010602011771号