改进初学者的PID-修改整定参数

　　最近看到了Brett Beauregard发表的有关PID的系列文章，感觉对于理解PID算法很有帮助，于是将系列文章翻译过来！在自我提高的过程中，也希望对同道中人有所帮助。作者Brett Beauregard的原文网址：http：//brettbeauregard.com/blog/2011/04/improving-the-beginner%E2%80%99s-pid-tuning-changes/

 

1、问题

　　对于任何可靠的PID算法，拥有在系统运行时更改整定参数的能力都是必须的。

 

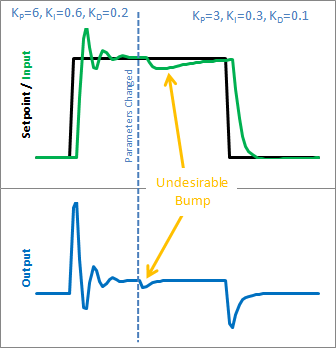
　　如果你试图在系统运行时改变整定参数，在初学PID的人看来会显得有点疯狂。让我们看看这是为什么？以下是初学者的 PID 在上述参数更改前后的状态：

 

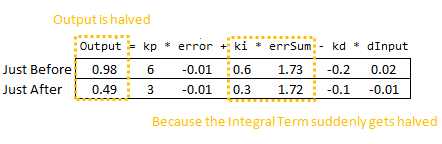
　　因此，我们可以立即将这种差异归咎于积分项(或“I项”)。只有当参数发生变化时，它才会发生剧烈的变化。为什么会这样？这与初学积分的人对积分的理解有关：

 

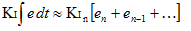
　　这种解释在 Ki 被改变之前都是可以正常工作的。然后，你突然把这个新的 Ki 乘以你积累的整个误差总和。这不是我们想要的！我们只想影响事情后续的发展。

2、解决方案

　　有几种方法可以处理这个问题。我在上一个库中使用的方法是重新缩放偏差累计。Ki 翻了一倍？或者把偏差累计削减一半。这可以避免积分项撞击，并且也能工作的很好。不过，这有点笨拙，我想出了更优雅的东西。(我不可能是第一个想到这个问题，但我确实是一个人想到的。这算数!)

　　这个方案需要一个小的基本代数 (还是微积分？)

 

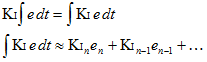
　　我们不是让 Ki 处在积分之外，而是把它带到里面。看起来我们视乎什么都没做，但我们会看到，在实践中，这带来了很大的变化。

　　现在，我们把误差乘以那个时候的Ki。然后我们存储它的和。当Ki发生变化时，没有任何变化，因为所有旧的Ki都已经“存在银行”了。我们得到一个平稳的转换，没有额外的数学运算。这可能会让我成为一个极客，但我觉得这很性感。

3、代码

 1 /*working variables*/
 2 unsigned long lastTime;
 3 double Input，Output，Setpoint;
 4 double ITerm，lastInput;
 5 double kp，ki，kd;
 6 int SampleTime = 1000; //1 sec
 7 void Compute()
 8 {
 9    unsigned long now = millis();
10    int timeChange = (now - lastTime);
11    if(timeChange>=SampleTime)
12    {
13       /*Compute all the working error variables*/
14       double error = Setpoint - Input;
15       ITerm += (ki * error);
16       double dInput = (Input - lastInput);
17  
18       /*Compute PID Output*/
19       Output = kp * error + ITerm - kd * dInput;
20  
21       /*Remember some variables for next time*/
22       lastInput = Input;
23       lastTime = now;
24    }
25 }
26  
27 void SetTunings(double Kp，double Ki，double Kd)
28 {
29   double SampleTimeInSec = ((double)SampleTime)/1000;
30    kp = Kp;
31    ki = Ki * SampleTimeInSec;
32    kd = Kd / SampleTimeInSec;
33 }
34  
35 void SetSampleTime(int NewSampleTime)
36 {
37    if (NewSampleTime > 0)
38    {
39       double ratio  = (double)NewSampleTime
40                       / (double)SampleTime;
41       ki *= ratio;
42       kd /= ratio;
43       SampleTime = (unsigned long)NewSampleTime;
44    }
45 }

　　因此，我们用复合积分项变量替换了 [第4行]偏差求和变量。它计算 Ki * 偏差，而不仅仅是偏差 [第15行]。此外，由于 Ki 现在被隐藏在积分项中，因此它将从主 PID 计算 [第19行] 中删除。

4、结果

 

 

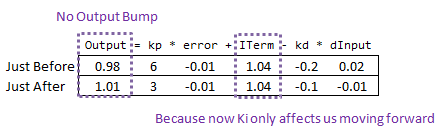
　　那么，这是如何解决问题的。在修改Ki之前，它重新计算了所有偏差的总和；我们看到的每一个偏差值。有了这段代码，之前的偏差将保持不变，而新的Ki只会影响事情的进展，这正是我们想要的。

译注：对于本篇讨论的修改整定参数对积分项的影响问题。采用位置式PID公式确实存在这一问题，作者的解决方式也很赞。因为这就是增量式PID积分项的默认处理方式。所以如果采用增量式PID就不会存在这个问题了。

欢迎关注：

posted @ 2019-08-04 09:00  Moonan  阅读(2039)  评论(0)  编辑  收藏  举报