P4649 [IOI2007] training 训练路径
P4649 [IOI2007] training 训练路径
题意：
给你一棵 \(n\) 个节点的树，上面还有 \(m-(n-1)\) 条非树边，每条非树边有一个代价 \(c_i\)，要求你删掉若干条非树边使得之后的这棵树满足不存在任意一个长度为偶数的简单环。保证每个节点度数 \(\le 10\)。
trick：如果树上不存在偶环，那么树上任意两个奇环之间没有公共边。
- 考虑到假如树上两个奇环之间有公共边，设这两个奇环的长度是 \(x,y\)，公共部分长 \(k\)，那么 \(x+y-2k\) 一定是偶数，换言之诞生了一个偶环，假设不成立。
30pts 链：
-
知道了这个 trick 后我们可以做这道题了。
-
首先删边对于判断是否存在满足条件的环对我们来说是一个困难的问题，但是加边就相对简单一些。
-
因此我们考虑要加入哪些非树边，使得加入的边权和最大，最后再拿总边权减去选择加入的非树边即可。
-
对于链的部分分，每条非树边连接的两点构成一个区间，环两两无交就是不存在一个点被两个区间覆盖；不能出现偶环只需要在加入非树边 \((u,v)\) 时确保链上 \(dist(u,v)\) 是偶数即可。
-
我们可以直接 dp，设 \(dp_i\) 表示进行了前 \(i\) 个区间的选择，第 \(i\) 个位置已被覆盖的最大边权和。转移：
-
\[\begin{align} dp_i + w(u,v) & \to dp_v &\text{if $i \leq u$} \end{align} \]
-
直接暴力选边就行，复杂度 \(O(nm)\)
100pts 树
-
树比链困难的地方在于树要考虑兄弟节点。
-
我们发现我们还有节点度数 \(\leq 10\) 的限制没有用上，我们可以延续链的思路，直接把 \(10\) 个兄弟看成同时操作 \(10\) 条链来解决，那么我们可以直接在 dp 里进行状压。
-
设 \(dp_{u,S}\) 表示以 \(u\) 为根的子树中，不考虑 \(S\) 集合中的儿子的子树的最大和。
-
至于这里为什么使用
不考虑，之后会再提到。 -
对于每个非树边显然要在两点的 lca 处进行 dp 考虑。这里要分两种情况：
-
不选择 \((u,v)\) 这条非树边：那么有 \(dp_{lca,S} = \sum_{v \notin S} dp_{v,0}\)
-
选择 \((u,v)\) 这条非树边：
-
这时候 \(u \to v \to lca \to u\) 成为一个奇环。
-
那么我们要加上排除掉这个奇环里所有点外其他节点产生的贡献。
-
设 \(u,v\) 两点分别在 \(lca\) 第 \(x,y\) 儿子子树内。可以得到
-
\[dp_{lca,S} = dp_{lca,S+x+y} + dp_{u,0} + dp_{v,0} + \sum_{t \in path(u,v)}^{fa(t) \neq lca, t \neq lca} dp_{fa(t),t} + w(u,v) \]
-
-
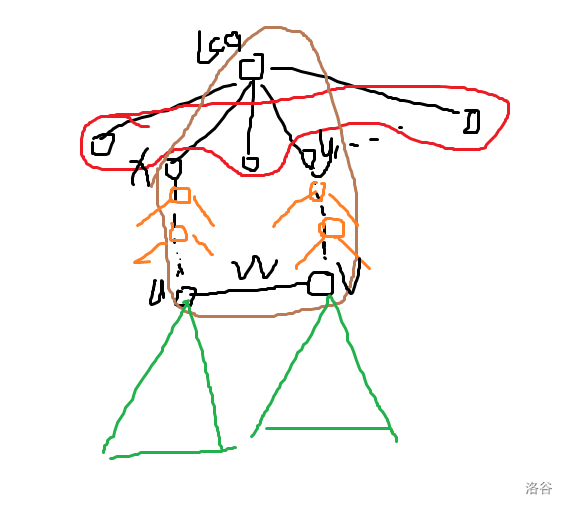
其中第一部分是如图红色部分，表示除了这两个儿子子树外其他儿子产生的贡献。
-
第二三部分为图中绿色部分，表示这个奇环的底部 \(u,v\) 两点两颗子树产生的贡献
-
第四部分为图中橙色部分，表示奇环从 \(u \to lca \to v\) 的路径上分叉出去的部分产生贡献
-
第五部分就是加入非树边的贡献。
-
-
-
可以注意到第四部分我们只需要去除掉 \(t\) 的一个儿子，这就是为什么我们使用
不考虑定义 dp 式子。实际上考虑也是可以做的，只不过要麻烦一点。 -
第四个式子暴力是没法算的，会直接 TLE 掉。但是我们可以把它拆成 \(u \to lca\) 和 \(v \to lca\) 两部分。设 \(val_u\) 表示从当前节点到 \(u\) 的路径上的 \(dp\) 之和，这样可以做到 \(O(nm)\)。
-
更好的，如果用一些启发式合并 + 打整体加法标记的方法应该可以做到 \(O(m \log n)\)。
-
最终答案为 \(\sum w_i - dp_{1,0}\)。
-
最终复杂度为 \(O(mn + m \times 2^{10})\) 或 \(O(m \log n + m \times 2^{10})\)。
-
最后要注意一些细节，例如当 \(u,v\) 中某一个本身就是 \(lca\) 时，贡献只需要加上 \(dp_{v,0}\) 和 \(val_{v}\)；以及处理第二种情况时，要按照集合 \(1\) 的数量从多到少来算。
Code：
- 这里我比较懒，写的 \(O(mn)\) 的做法
#include <bits/stdc++.h>
#define ll long long
#define ckmax(a, b) (a = max(a, b))
#define MP make_pair
#define pcn putchar('\n')
#define fi first
#define se second
using namespace std;
const int maxn = 1000;
const int maxm = 5000;
const int maxlg = 10;
const int maxs = 10;
const int max2s = (1 << 10);
const int INT = 1e9 + 50;
int n, m;
struct E{int v, w, id, nx;} e[maxm * 2 + 50];
int hd[maxn + 50], cnt = 1;
map<pair<int, int>, int> edge; // 用于寻找 (u, v) 这条边的编号
struct E2{int u, v, x, y, w;}; // 非树边的 (u, v)，是 lca 的第 x, y 编号的儿子，边权为 w
vector<E2> e_lca[maxn + 50];
bool vis[maxm * 2 + 50];
int fa[maxn + 50], pos[maxn + 50][maxs + 5]; // pos[u][i] 是 u 子树中第 i 个儿子在前向星的位置
int fa2[maxn + 50][maxlg + 5], dep[maxn + 50], lg[maxn + 50]; // 倍增 LCA
vector<int> T(max2s); // 长度为 10 的集合按照 1 个数从大到小排列
int val[maxn + 50], dp[maxn + 50][max2s + 50];
void ade(int u, int v, int w){
e[++ cnt] = E{v, w, 0, hd[u]};
hd[u] = cnt;
edge[MP(u, v)] = cnt;
}
void Ade(int u, int v, int w){
ade(u, v, w), ade(v, u, w);
}
void dfs(int u, int father){
vis[u] = true;
fa[u] = father;
dep[u] = dep[father] + 1;
int cntid = 0;
for(int i = hd[u]; i; i = e[i].nx){
int v = e[i].v, w = e[i].w;
if(vis[v] || w) continue;
// 预处理每条树边的编号
e[i].id = e[i ^ 1].id = cntid ++;
pos[u][e[i].id] = i;
dfs(v, u);
}
}
void LCA_Init(){
for(int i = 1; i <= n; ++ i){
fa2[i][0] = fa[i];
}
for(int j = 1; j <= lg[n]; ++ j){
for(int i = 1; i <= n; ++ i){
fa2[i][j] = fa2[fa2[i][j - 1]][j - 1];
}
}
}
// 返回 u, v 跳到 lca 的两个儿子
pair<int, int> LCA(int u, int v){
if(dep[u] < dep[v]) swap(u, v);
for(int i = lg[dep[u] - dep[v]]; i >= 0; -- i){
if(dep[fa2[u][i]] > dep[v]){
u = fa2[u][i];
}
}
if(fa[u] == v) return MP(u, u);
if(dep[u] != dep[v]) u = fa[u];
for(int i = lg[dep[u]]; i >= 0; -- i){
if(fa2[u][i] != fa2[v][i]){
u = fa2[u][i];
v = fa2[v][i];
}
}
return MP(u, v);
}
int dist(int a, int b, int lca){
return dep[a] + dep[b] - 2 * dep[lca];
}
void getValue(int u){
for(int i = hd[u]; i; i = e[i].nx){
int v = e[i].v, w = e[i].w;
if(v == fa[u] || w) continue;
val[v] = val[u] + dp[u][1 << e[i].id];
getValue(v);
}
}
void dfs2(int u){
val[u] = 0;
for(int i = hd[u]; i; i = e[i].nx){
int v = e[i].v, w = e[i].w;
if(v == fa[u] || w) continue;
dfs2(v);
val[v] = 0;
getValue(v);
}
// 计算不选非树边的情况
for(int S = 0; S < max2s; ++ S){
for(int i = 0; i < 10; ++ i){
if((S >> i & 1) == 0){
dp[u][S] += dp[e[pos[u][i]].v][0];
// 这里如果 in[u] < 10，那么 pos[u][i] 为 0，不会对答案产生贡献
}
}
}
// 计算选树边的情况
for(auto S : T){
for(auto j : e_lca[u]){
if((S >> j.x & 1) || (S >> j.y & 1)) continue;
if(j.x != j.y){
// u, v 自己都不是 lca
ckmax(dp[u][S], dp[u][S | (1 << j.x) | (1 << j.y)] + dp[j.u][0] + dp[j.v][0] + j.w + val[j.u] + val[j.v]);
}
else{
// u, v 有一个是 lca
ckmax(dp[u][S], dp[u][S | (1 << j.x) | (1 << j.y)] + dp[dep[j.u] > dep[j.v] ? j.u : j.v][0] + j.w + val[j.u] + val[j.v]);
}
}
}
}
int main(){
lg[0] = -1;
for(int i = 2; i <= maxn + 30; ++ i){
lg[i] = lg[i >> 1] + 1;
}
// 集合按照元素个数从大到小枚举
for(int S = 0; S < max2s; ++ S){
T[S] = S;
}
sort(T.begin(), T.end(), [](int x, int y){
return __builtin_popcount(x) > __builtin_popcount(y);
});
scanf("%d%d", &n, &m);
int u, v, w, sumw = 0;
for(int i = 1; i <= m; ++ i){
scanf("%d%d%d", &u, &v, &w);
Ade(u, v, w);
sumw += w;
}
dfs(1, 0);
LCA_Init();
for(int i = 1; i <= n; ++ i){
vis[i] = false;
}
// 求出每条边由谁来处理
for(int u = 1; u <= n; ++ u){
for(int i = hd[u]; i; i = e[i].nx){
int v = e[i].v, w = e[i].w;
if(vis[i] || !w) continue;
vis[i] = vis[i ^ 1] = true;
pair<int, int> t = LCA(u, v);
int lca = fa[t.fi];
// 去除构成偶环的非树边
if((dep[u] + dep[v] - (dep[lca] << 1) & 1) == 0){
e_lca[lca].push_back(E2{u, v, e[ edge[MP(lca, t.fi)] ].id, e[ edge[MP(lca, t.se)] ].id, w});
}
}
}
dfs2(1);
printf("%d\n", sumw - dp[1][0]);
return 0;
}
