单调栈POJ-2559
单调栈POJ-2559
Description
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:
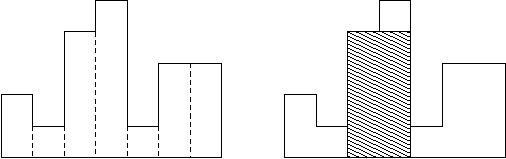
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Input
The input contains several test cases. Each test case describes a histogram and starts
with an integer n, denoting the number of rectangles it is composed of. You may assume
that 1<=n<=100000. Then follow n integers h1,...,hn, where 0<=hi<=1000000000.
These numbers denote the heights of the rectangles of the histogram in left-to-right
order. The width of each rectangle is 1. A zero follows the input for the last test case.
Output
For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.
Sample Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
Sample Output
8
4000
#include<stack>
#include<cstdio>
using namespace std;
typedef long long ll;
#define rep(i,x,y) for(register int i=x;i<=y;++i)
#define gc getchar()
template<class T>
inline void read(T&x) {
x=0;
char ch=gc;
bool flag=0;
while(ch<'0'||ch>'9') {flag|=(ch=='-'),ch=gc;}
while(ch>='0'&&ch<='9') {x=x*10+ch-48,ch=gc;}
x=flag?-x:x;
}
ll ans,rlen;//rlen,右边的比当前高的矩形的总宽度
struct N {
ll w,h;
} x;
stack<N>s;
int main() {
//freopen("in.txt","r",stdin);
int n;
while(1) {
read(n);
if(!n)
break;
ans=rlen=0;//初始化
rep(i,0,n-1) {
read(x.h),x.w=1;//width 默认为1
if(!s.empty()&&x.h<(s.top()).h) {
rlen=0;
while(!s.empty()&&x.h<(s.top()).h) {
rlen+=s.top().w;//以当前矩形为标准,向右扩展,左边更矮,扩展不了。
ans=max(s.top().h*rlen,ans);//以当前矩形的高作为高,更新ans
s.pop();
}
x.w+=rlen;//相当于比x.h高的都截成和x.h一样
}
s.push(x);
}
x.h=x.w=0;
while(!s.empty()) {
x.w+=s.top().w;
x.h=s.top().h;
ans=max(x.h*x.w,ans);
s.pop();
}
printf("%lld\n",ans);
}
return 0;
}
小A的柱状图
题目描述
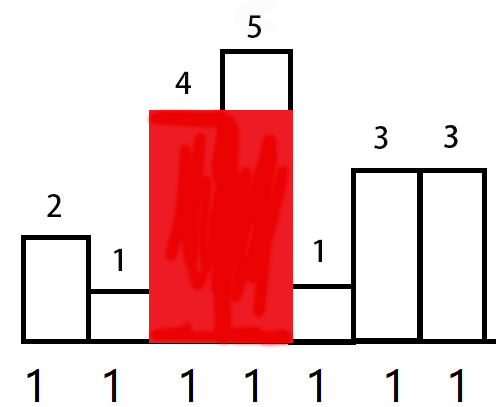
柱状图是有一些宽度相等的矩形下端对齐以后横向排列的图形,但是小A的柱状图却不是一个规范的柱状图,
它的每个矩形下端的宽度可以是不相同的一些整数,分别为a[i]a[i],每个矩形的高度是h[i]h[i],现在小A只想知道
在这个图形里面包含的最大矩形面积是多少。
输入描述:
一行一个整数N,表示长方形的个数
接下来一行N个整数表示每个长方形的宽度
接下来一行N个整数表示每个长方形的高度
输出描述:
一行一个整数,表示最大的矩形面积
输入
7
1 1 1 1 1 1 1
2 1 4 5 1 3 3
输出
8
备注:
1≤n≤1e6,1≤a[i]≤100,1≤h[i]≤1e9
直接改几个数字就行了
#include<stack>
#include<cstdio>
using namespace std;
typedef long long ll;
#define rep(i,x,y) for(register int i=x;i<=y;++i)
#define gc getchar()
template<class T>
inline void read(T&x) {
x=0;
char ch=gc;
bool flag=0;
while(ch<'0'||ch>'9') {
flag|=(ch=='-'),ch=gc;
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-48,ch=gc;
}
x=flag?-x:x;
}
ll ans,rlen;
const int maxn=1e6+5;
ll W[maxn];
struct N {
ll w,h;
} x;
stack<N>s;
int main() {
freopen("in.txt","r",stdin);
int n;
read(n);
ans=rlen=0;
rep(i,0,n-1)
read(W[i]);
rep(i,0,n-1) {
read(x.h),x.w=W[i];
if(!s.empty()&&x.h<(s.top()).h) {
rlen=0;
while(!s.empty()&&x.h<(s.top()).h) {
rlen+=s.top().w;
ans=max(s.top().h*rlen,ans);
s.pop();
}
x.w+=rlen;
}
s.push(x);
}
x.h=x.w=0;
while(!s.empty()) {
x.w+=s.top().w;
x.h=s.top().h;
ans=max(x.h*x.w,ans);
s.pop();
}
printf("%lld\n",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号