Tensorflow 中的优化器解析

Tensorflow:1.6.0

优化器（reference:https://blog.csdn.net/weixin_40170902/article/details/80092628）

           I:  tf.train.GradientDescentOptimizer  Tensorflow中实现梯度下降算法的优化器。

           梯度下降：（1）标准梯度下降GD（2）批量梯度下降BGD（3）随机梯度下降SGD

           (1)标准梯度下降：学习训练的模型参数为W，代价函数为J(W)，则代价函数关于模型参数的偏导数即相关梯度为dJ(W)，学习率为eta,梯度下降法更新参数公式：

                               

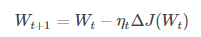
          模型参数的调整沿着梯度方向不断减小的方向最小化代价函数。基本策略：在有限视野内寻找最快下山路径，每迈出一步参考当前位置最陡的梯度方向，从而决定下一步。

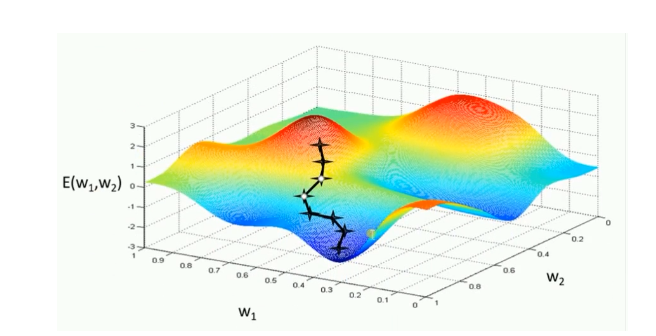
          评价：GD的两个缺点

                  （1）训练速度慢：每进行一步都要计算调整下一步方向，在大型数据中，每个样本都更新一次参数，且每次迭代要遍历所有样本，需要很长时间进行训练和达到收敛。

                  （2）易陷入局部最优解：在有限的范围内寻找路径，当陷入相对较平的区域，误认为最低点（局部最优即鞍点），梯度为0，不进行参数更新。

 

          （2）批量梯度下降BGD：学习训练样本的总数为n,每次样本i形式为（Xi,Yi），模型参数为W，代价函数为J(W)，每个样本i的代价函数关于W的梯度为dJi（Wt,Xi,Yi），学习率eta_t,跟新参数表达式为：     

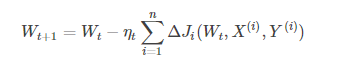          模型参数的更新与全部输入样本的代价函数和有关。每次权重的更新发生在批量输入样本之后，大大加快训练速度。

          评价：BGD比GD训练时间短，而且每次下降的方向都很正确。

#-*- coding: utf-8 -*-
#BGD python 实现
import random
#用y = Θ1*x1 + Θ2*x2来拟合下面的输入和输出
#input1  1   2   5   4
#input2  4   5   1   2
#output  19  26  19  20
input_x = [[1,4], [2,5], [5,1], [4,2]]  #输入
y = [19,26,19,20]   #输出
theta = [1,1]       #θ参数初始化
loss = 10           #loss先定义一个数，为了进入循环迭代
step_size = 0.01    #步长
eps =0.0001         #精度要求
max_iters = 10000   #最大迭代次数
error =0            #损失值
iter_count = 0      #当前迭代次数
 
err1=[0,0,0,0]      #求Θ1梯度的中间变量1
err2=[0,0,0,0]      #求Θ2梯度的中间变量2
 
while( loss > eps and iter_count < max_iters):   #迭代条件
    loss = 0
    err1sum = 0
    err2sum = 0
    for i in range (4):     #每次迭代所有的样本都进行训练
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]  #预测值
        err1[i]=(pred_y-y[i])*input_x[i][0]
        err1sum=err1sum+err1[i]
        err2[i]=(pred_y-y[i])*input_x[i][1]
        err2sum=err2sum+err2[i]
    theta[0] = theta[0] - step_size * err1sum/4  #对应5式
    theta[1] = theta[1] - step_size * err2sum/4  #对应5式
    for i in range (4):
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]   #预测值
        error = (1/(2*4))*(pred_y - y[i])**2  #损失值
        loss = loss + error  #总损失值
    iter_count += 1
    print ("iters_count", iter_count)
print ('theta: ',theta )
print ('final loss: ', loss)
print ('iters: ', iter_count)

           （3）随机梯度下降法（SGD）：从一批训练样本n中随机选取一个样本i，模型参数为W，代价函数为J(W)，梯度为dJ(W)，学习率为eta,则使用SGD进行更新参数公式为：

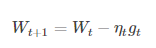
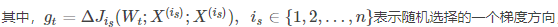
                  SGD不需要每一步都计算梯度，但最终能达到低点，只是过程会比较崎岖。

 

          评价：优点：计算梯度快，对于小噪声，SGD可以很好收敛。对于大型数据，训练很快，从数据中取大量的样本算一个梯度，更新一下参数。

                     缺点：在随机选择梯度时会引入噪声，权值更新方向可能出现错误。SGD未能克服全局最优。 

#-*- coding: utf-8 -*-
#SGD-python实现
import random
#用y = Θ1*x1 + Θ2*x2来拟合下面的输入和输出
#input1  1   2   5   4
#input2  4   5   1   2
#output  19  26  19  20
input_x = [[1,4], [2,5], [5,1], [4,2]]  #输入
y = [19,26,19,20]   #输出
theta = [1,1]       #θ参数初始化
loss = 10           #loss先定义一个数，为了进入循环迭代
step_size = 0.01    #步长
eps =0.0001         #精度要求
max_iters = 10000   #最大迭代次数
error =0            #损失值
iter_count = 0      #当前迭代次数
 
while( loss > eps and iter_count < max_iters):    #迭代条件
    loss = 0
    i = random.randint(0,3)  #每次迭代在input_x中随机选取一组样本进行权重的更新
    pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1] #预测值
    theta[0] = theta[0] - step_size * (pred_y - y[i]) * input_x[i][0]
    theta[1] = theta[1] - step_size * (pred_y - y[i]) * input_x[i][1]
    for i in range (3):
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1] #预测值
        error = 0.5*(pred_y - y[i])**2
        loss = loss + error
    iter_count += 1
    print ('iters_count', iter_count)
print ('theta: ',theta )
print ('final loss: ', loss)
print ('iters: ', iter_count)

          II tf.train.MomentumOptimizer tensorflow中实现动量优化算法的优化器

           动量优化算法在梯度下降法的基础上进行改变，具有加速梯度下降的作用。类别：（1）标准动量优化方法Momentum,(2)NAG动量优化方法（NAG在Tensorflow中与Momentum合并在同一函数tf.train.MomentumOptimizer中，可以通过参数配置启用。）

         （1）Momentum:引入一个累计历史梯度信息动量加速SGD。优化公式如下：

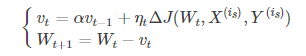
             alpha代表动力大小，一般取为0.9（表示最大速度10倍于SGD）。动量解决SGD的两个问题：（1）SGD引入的噪声（2）Hessian矩阵病态（SGD收敛过程的梯度相比正常来回摆动幅度较大）

            当前权值的改变受上一次改变的影响，类似加上了惯性。

         （2）NAG：牛顿加速梯度算法是Momentum变种，更新公式如下：

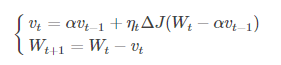
            NAG的计算在模型参数施加当前速度之后，可以理解为在Momentum 中引入了一个校正因子。

            在Momentum中，小球会盲目的跟从下坡的梯度，易发生错误。因此，需要提前知道下降的方向，同时，在快到目标点时速度会有所下降，以不至于超出。

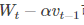     可以表示小球下一个大概的位置，从而知道下一个位置的梯度，然后使用当前位置来更新参数。NGD对凸批量梯度的收敛效果较大，而对NAG的效果作用不大。

           III自适应学习率优化算法：传统的优化算法将学习率设置为常数或者根据训练次数调节学习率。忽略了学习率其他变化的可能性。（1）AdaGrad(2)RMSProp（3）Adam(4)AdaDelta

           (1)AdaGrad算法：（tf.train.AdgradOptimizer）

            独立适应所有模型参数的学习率，缩放每个参数反比于其所有梯度历史平均值总和的平方根。具有代价函数最大梯度的参数相应的有快速下降的学习率，而小梯度的参数在学习率上有相对较小的下降。

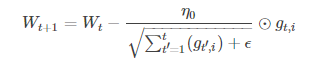
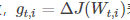g_t,i代表t时刻，指定类别i，代价函数关于W的梯度。对于较高类别的数据，Adagrad给与越来越小的学习率，对于较少的类别数据，给予较大的学习率。Adagrad适用于数据稀疏或者分布不平衡的数据集。

        评价：优点：无需人为调节学习率，可以自动调节。缺点；随着迭代次数增多，学习率越来越小，最终趋于0。

           (2）RMSProp算法(tf.train.RMSPropOptimizer)

            修改了AdaGrad的梯度累积为指数加权的移动平均，使在非凸下效果更好。

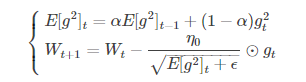
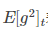代表前t次的梯度平方的均值。RMSProp的分母取了加权平均，避免学习率越来越低，同时可以自适应调节学习率。

          （3）AdaDelta算法(tf.train.AdadeltaOptimizer)：AdaGrad与RMSProp都需要指定全局学习率，AdaDelta结合两种算法每次参数的更新步长

    

 

           评价：在训练的前中期，表现效果较好，加速效果可以，训练速度更快。在后期，模型会反复地在局部最小值附近抖动。

          （4）Adam算法(tf.train.AdamOptimizer)：动量直接并入了梯度一阶矩（指数加权）的估计。相比于，RMSProp缺少修正因子导致二阶矩估计在训练初期有较高的偏置，Adam包括偏置修正，从原始点初始化的一阶矩（动量项）和（非中心的）二阶矩估计。

           评价：Adam对超参数的选择相当鲁棒。

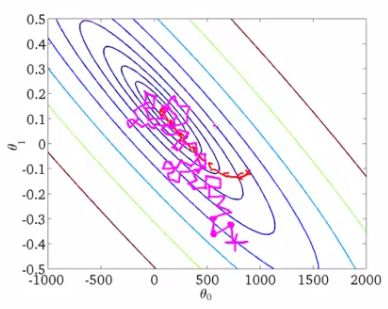
不同优化器比较

         下降速度上，三个自适应学习优化器  AdaGrad,RMSProp与AdaDelta的下降速度明显快于SGD，而Adagrad与RMSProp速度相差不大快于AdaDelta。两个动量优化器Momentum ,NAG初期下降较慢，后期逐渐提速，NAG后期超过Adagrad与RMSProt。

        在有鞍点的情况下，自适应学习率优化器没有进入，Momentum与NAG进入后离开并迅速下降。而SGD进入未逃离鞍点。

       速度：快->慢： Momenum ，NAG -> AdaGrad,AdaDelta,RMSProp ->SGD

       收敛： 动量优化器有走岔路，三个自适应优化器中Adagrad初期走了岔路，但后期调整，与另外两个相比，走的路要长，但在快接近目标时，RMSProp抖动明显。SGD走的过程最短，而且方向比较正确。