论文阅读笔记一：Tutorial on Gabor Filters

时域下的一维Gabor滤波器：

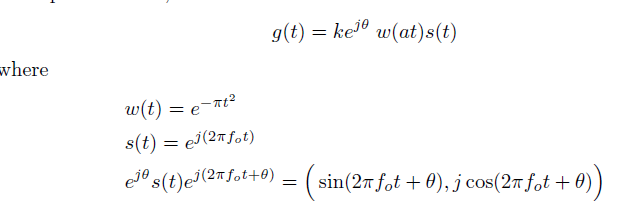
可以将Gabor滤波器看作是两个输出两个相位的滤波器，分别在实数域和虚数域上。

实数域上滤波器为：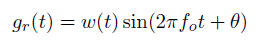

虚数域上滤波器为：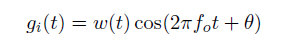

傅里叶变换为频域：

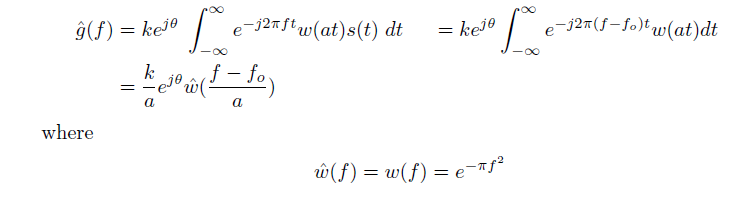
上述两个滤波器对频率敏感，为了获得一个对相位不敏感，而且对正弦输入无正面响应的响应，因此，通过计算两个滤波器输出的和的平方根来得到这样一个滤波器。

在频率域上，针对一个特定频率的响应能量只是傅里叶变换的能量。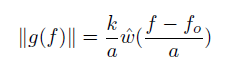       

上述式子为gaussian 函数，中心为fo，宽度比例为a。

频率带宽和峰值响应

峰值响应在频率为f_o处，

半个能量级的频率为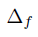

 

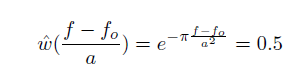
因此

所以带宽为约等于 2*0.5a = a，所以a可以被解释为半能量滤波器的带宽。

直流电响应的消除

通过调节f_o 和a可以获得较大的直流响应。为了排除直流响应通过减去一个低通高斯滤波器的输出操作。

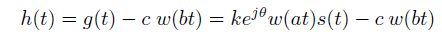
傅里叶变换后：

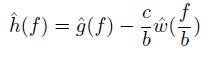
通过一系列推导，得到当b=a时，满足条件，解得：

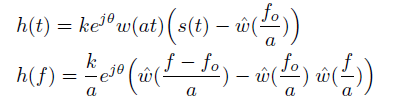
空间二维滤波

函数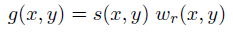：，其中s(x,y)为载波（正弦函数），w_r（x,y）为二维高斯形状的滤波函数，如包络线。

 

载波

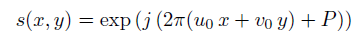
（u₀,v₀）定义空间频率，P定义正弦曲线的相位

可以将载波函数看作实轴和虚轴上的两个函数

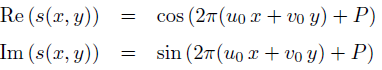
u₀,v₀  定义正弦曲线在笛卡尔坐标系下的空间频率。空间频率也可以在极坐标下描述为能量F₀和方向w₀

ie

载波通过上述变换可以得到

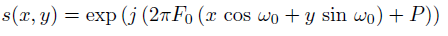
Gaussian 包络线

其中（x0,y0）为此函数的峰值，a，b为gaussian 尺度大小调节参数，下标r表示循环操作

 

形状如下：

                  

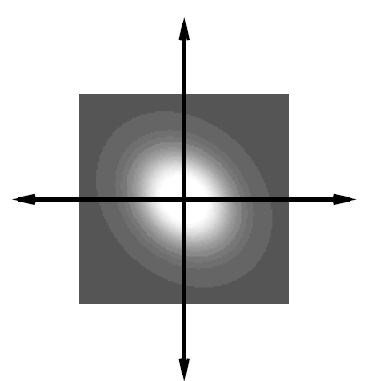
gaussian 函数主要由一下九个参数定义：

每一个Gabor函数都有两个正交的函数，分别为函数的实轴和虚轴部分。

形状如下：

                                    

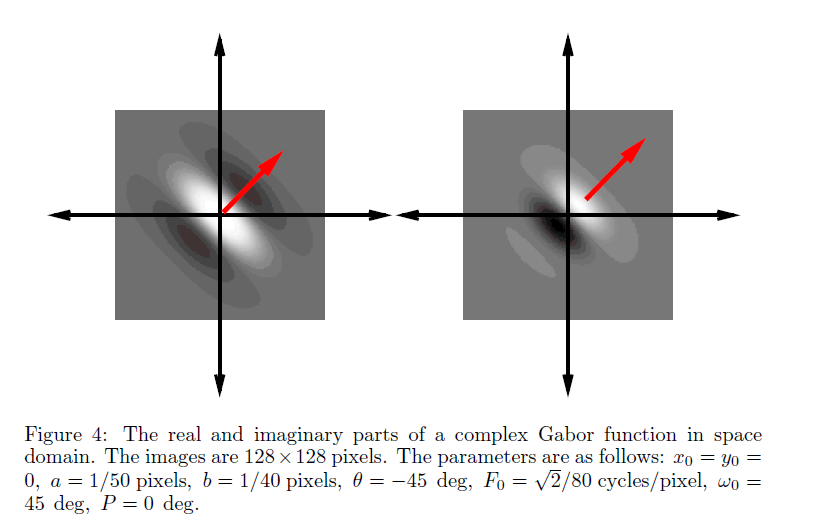
空域上的gabor函数为：

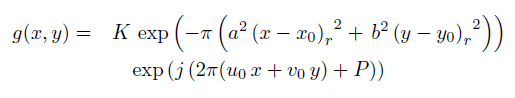
极坐标下的gabor函数为：

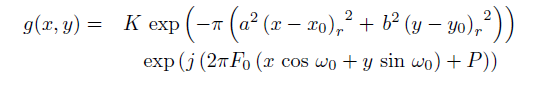
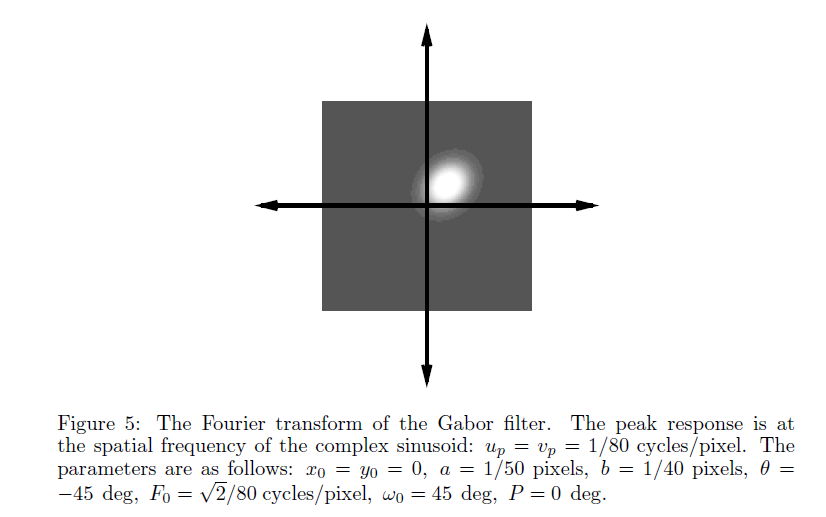
傅里叶变换以后的Gabor函数显示：

                                                 

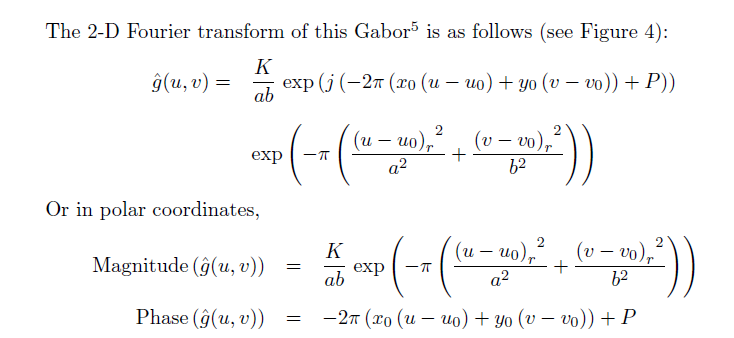
半能级描述

由于其大小等于峰值能级的一半，而峰值能级（极值）可以由以下获得，峰值（极值点）为（u，v） = (u0,v0),得到峰值能级为K/ab,

因此，只需找到一系列满足K/2ab的（u,v）的值。

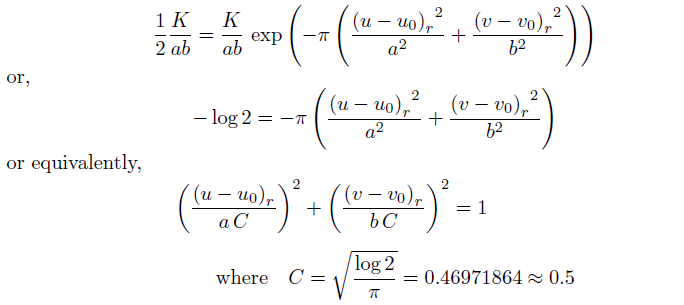
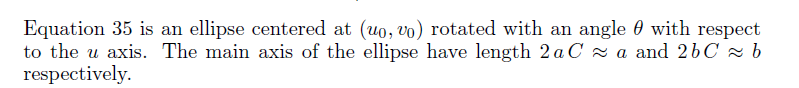
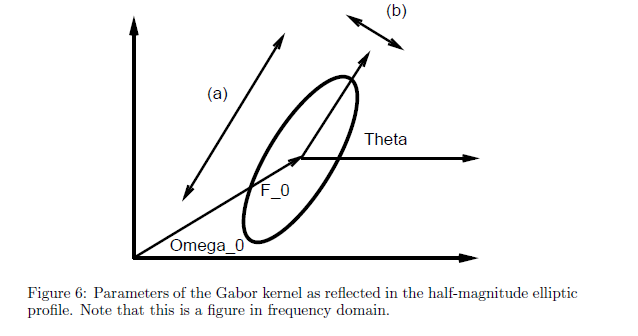
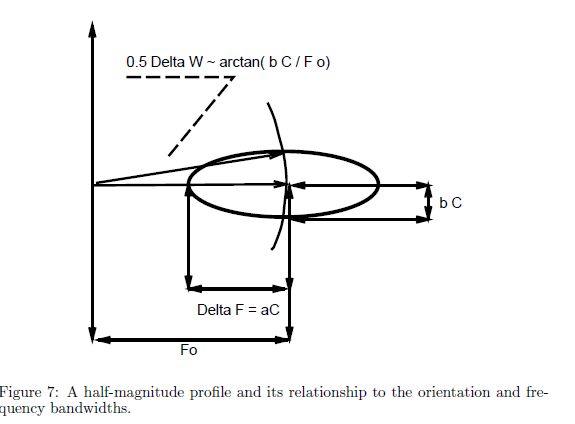
半能级频率和方向带宽

神经元半能级频率及方向带宽可以用于针对半能级响应的测量，假设优选神经元的空间频率u0,v0，

在极坐标下空间频率可以被表述为F0,w0.

我们通过用正弦图像的方向，不同空间频率能级来探测神经元，进而发现半能级频率带宽。

 通过增加F，直到能级的响应是在（F0,w0）处能级的一半。定义此时为F_max,

通过较小F,直到能级的响应是在（F0,w0）处能级的一半。定义此时为F_min

定义半能级频率宽度为：

          

或者在倍频下为：

              

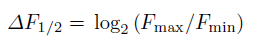
半能级方向带宽和半能级频率带宽相似，只是这里操作的是由F变为w

得到如下结果：

有效传播和均方根传播 

 一函数均方根的长度，宽度，和区域定义在他们的一阶矩和二阶矩

一个复杂函数g(x,y)的矩阵通过将这个函数转为概率密度（必须为正且和为1）然后计算其一阶矩和二阶矩（一阶矩就是随机变量的期望，二阶矩就是随机变量平方的期望）

通过g(x,y)，我们建立如下概率密度

                                

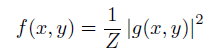
g(x,y)绝对值的平方为信号的能量级的平方，总是正的

Z保证累加和为1.0

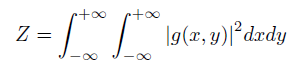
统计度量的位置和大小：

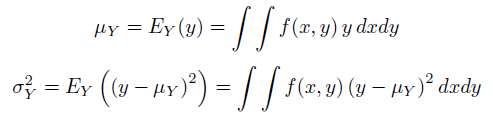
均方根的长度和宽度定义为一个旋转型的f(x,y)的，因此上述的旋转分布的协方差为0 。

让Xr Yr代表 协方差为0的旋转变量，均方根的长度和宽度为

                                                 

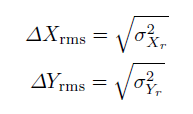
在频率域上通过傅里叶变换，得到的定义如下：

                                           

在空域和频率域上的均方根区域定义如下：

                                    

有效长度，宽度，区域只是乘上一个sqrt(2)*pi

在任何二维函数的限定条件下，有如下不等式：

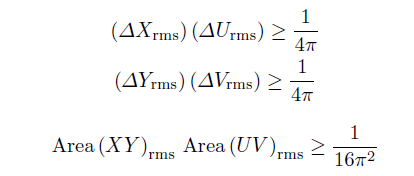
用Gabor函数可以很简单的证明这不确定关系的下限。对于在空间域上给定的一个区域，提供了在频率域上最大可能的分辨率，反之亦然。

Gabor函数的均方根宽度和长度为：

                                              

 

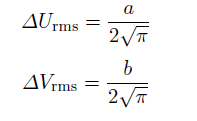
 将Gabor函数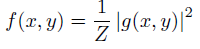的概率密度简单的考虑为Gaussian

方差为

由不确定关系可以得到
                             

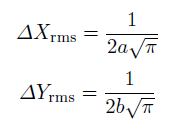
作为简单细胞感受野模型的Gabor函数（此章含有大量生物上由Gabor思想启发的设计文献，忽略此章的阅读）

7Gabor的空域滤波

考虑大量带有Gabor核函数及除了位置参数（x,y）的其他参数的感受野神经元。让这些神经元呈中心凹处均匀分布。

中心凹处的至少包含两个正交的神经元。我们可以模型化将一系列神经元的操作作为卷积操作（假设在中心凹处一个连续均匀分布的滤波器）。由于空域卷积是频率域的结果。Gabor的功能像是对中心凹处图像进行带通滤波。峰频由载波函数的空间频率控制（U0,V0）半能级区由高斯包络线的旋转角度，尺度参数a和b控制。

8能量滤波一个正交对是一系列两个具有相同振幅响应但相位响应移动90度的两个线性操作。严格的讲，sin,和cos的Gabor操作不是整觉对，因为cos相位Gabor具有一些直流响应。然而sin Gabor却没有。然而，可以让正交Gabor对看起来非常像sin/cos对。因此，sin和cos Gabor对被普遍当作是正交对。

能量机械学是累加正交对输出的平方的系统。对于随机正弦输入 ，能量机械有非调制响应。

9~end 只大体浏览未重点阅读